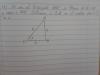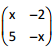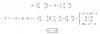Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Majo Artur ????
el 6/10/16

Que tal Unicoos me podrían ayudar con estos ejercicios, lo que pasa es que tengo una confusión ya que cuando tengo un ejercicio parecido a estos pero con el x cuadrada
lo resuelvo mediante diferencia de cuadrados y mi duda es que si usare ese mismo método para estos ejercicios o habrá un metodo de diferencia de cuartos y otro de quintos? explíquenme por favor gracias

••0 voto/s
•
Desencadenado
el 6/10/16
Jose utiliza Ruffini para factorizar con el número al que tiende la X. si quieres te hago uno para que veas ;-)

•1 voto/s
•
Desencadenado
el 6/10/16

•0 voto/s
•
Majo Artur ????
el 6/10/16
si por favor y se puede resolver con división sintética también?

•0 voto/s
•
Desencadenado
el 6/10/16

•0 voto/s
•

Cancelar
Cristian
el 6/10/16

Hola que tal queria saber si me pueden ayudar en este ejercicio...
b) Determina los máximos, mínimos y puntos de inflexión de la función

••0 voto/s
•
David
el 6/10/16
Tienes que hallar las raices o ceros de ese polinomio... Para ello, Ruffini o Cardano...
Formula de Cardano
Descomposición factorial
Como por Ruffini te será imposible, solo podrás hacer Cardano para obtener una de las raices. Las dos restantes podrás obtenerla haciendo una ecuación d segundo grado...
Nos cuentas ¿ok?

•0 voto/s
•

Cancelar
Bruno
el 6/10/16

Hola, queria saber si hay videos de como resolver matrices, busque y encontre pero nose si son especificos a una pregunta que le hicieron.

••0 voto/s
•
David
el 6/10/16
Sin saber que pregunta te hicieron....
De matrices y ecuaciones matriciales hay muchos vídeos

•0 voto/s
•

Cancelar
Facundo
el 6/10/16

Hola gente, me darian una mano con este ejercicio? Muchas gracias!

••0 voto/s
•
Antonio Silvio Palmitano
el 6/10/16
Veamos:
Consideramos la suma y el producto usuales en R, y la suma usual en R^2.
Pasamos a las propiedades del producto de vector por escalar.
Seudo distributividad con suma de vectores:
c*( (a,b) + (d,e) ) = c*(a+d,b+e) = ( c(a+d),0 ) = (ca+cd,0) = (ca,0) + (cd,0) = c(a,b) + c(d,e), se cumple.
Seudo distributividad con suma de esclares:
(c1 + c2)*(a,b) = ( (c1 + c2)a , 0 ) = (c1*a + c2*a , 0) = (c1*a,0) + (c2*a,0) = c1*(a,b) + c2*(a,b), se cumple.
Seudo asociatividad con producto de escalares:
(c1*c2)*(a,b) = ( (c1*c2)*a , 0 ) = ( c1*(c2*a) , 0 ) = c1*( c2 * (a,b) ), se cumple.
Seudo elemento neutro:
1*(a,b) = (1*a,0) = (a,0) que es distinto de (a,b), por lo tanto no se cumple, y la estructura no es espacio vectorial.
Espero haberte ayudado.

•0 voto/s
•

Cancelar
Diego Schwindt
el 6/10/16

Buenas tardes, necesitaría ayuda con esta expresion algebraica fraccionaria. Muchas Gracias

••0 voto/s
•
Desencadenado
el 6/10/16

•0 voto/s
•

Cancelar
Wayner
el 6/10/16

Unicoos necesito de su ayuda en este ejercicio:

••0 voto/s
•
Desencadenado
el 6/10/16
Wayner cual es el valor de DC, no logro verlo bien?

•0 voto/s
•
Wayner
el 6/10/16
Nelson El valor es 10raiz3

•0 voto/s
•
Desencadenado
el 6/10/16

•0 voto/s
•
Desencadenado
el 6/10/16

•0 voto/s
•
Aleking
el 6/10/16

•0 voto/s
•

Cancelar
Luis Antonio Carmona Garcés
el 6/10/16

Buenas alguien me puede ayudar.
Calcula el numero real x de forma que el numero complejo (x+2i)/(4-3i) este en la primera bisectriz del primer cuadrante

••0 voto/s
•
Antonio Silvio Palmitano
el 6/10/16
Recuerda que en el primer cuadrante x es positivo e y también es positivo, y que en la bisectriz del primer (y del tercer) cuadrante, tenemos que y es igual a x, por lo que la parte real del complejo debe ser igual a su parte imaginaria, y ambas partes deben ser positivas..
Luego, multiplicamos al numerador y al denominador por el conjugado de éste último.
El numerador queda: N = (x+2i)(4+3i) = 4x + 3xi + 8i - 6 = (4x - 6) + (3x + 8)i.
El denominador qued D = (4-3i)(4+3i) = 16 + 9 = 25.
Luego, la parte real de la expresión queda: (4x - 6)/25, y la parte imaginaria queda: (3x +8)/25.
Luego, para cumplir las condiciones del enunciado, planteamos:
(4x - 6)/25 = (3x +8)/25, cancelamos denominadores comunes y queda:
4x - 6 = 3x + 8, hacemos pasaje de términos, reducimos términos semejantes y queda:
x = 14.
Espero haberte ayudado.

•0 voto/s
•

Cancelar
Wayner
el 6/10/16
1. Buenas uniccoos, me podrian ayudar en este ejercicio de triangulos? La respuesta es: 5
••0 voto/s
•
Antonius Benedictus
el 6/10/16
Te ayudamos, Wayner.

•0 voto/s
•

Cancelar
Javier
el 5/10/16

Hola, como se haría esto? Gracias!
Estudiar para qué valores de x, la matriz inversa de coincide con su opuesta.

••1 voto/s
•
Alex Domínguez
el 5/10/16
Haz la opuesta, le haces el determinante y este lo igualas al determinante de esta y el valor de x será ese

•1 voto/s
•
Javier
el 5/10/16
Gracias por responder, pero es que me sale -x^2+10 en los dos y no se seguir...

•1 voto/s
•
Daixmaan
el 5/10/16
Alex estamos haciendo eso y no sale. Nos sale -x²+ 10 en ambos determinantes.

•0 voto/s
•
Antonius Benedictus
el 5/10/16
Va, Javier.

•1 voto/s
•
Javier
el 5/10/16
Muchas gracias!

•0 voto/s
•

Cancelar