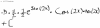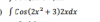-
Wayner
el 1/10/16Unicoos necesito la ayuda para llegar a la respuesta de este ejeecicio. Por lo qie veo tengo un planteamoento bueno. Pero no llego al resultado. La Resp.: es raiz 2/4 × (raiz 3 -1). De rodas formas esta en la foto.
-
Gaussiano
el 1/10/16 -
Fabricio
el 1/10/161.- Comprobar si es o no un sistema de generadores de IR4 el conjunto
S = { u1 = (1, 2, 1, 1), u2 = (−1, 2, 3, 5), u3 = (0, 2, 2, 3), u4 = (3, 4, 0, −1), u5 = (1, 8, 6, 9)}
Encontrar, si es posible, un vector de IR4 que no pertenezca al subespacio lin(S)
-
Pablo Reyes
el 1/10/16Hola buenas tardes. Planteo el siguiente ejercicio,no entiendo es el por qué:
Si E > 0
¿Qué conjunto de puntos representa 0 < x -a (en valor absoluto) < E?
siendo a ∈ R ?
Solución: Para todo x perteneciente al conjunto (a-E, a+E) excepto a.
Cómo lo ha hecho y por qué excluye a
Antonio Silvio Palmitano
el 1/10/16Observa que si x = a, la desigualdad queda:
0 < |a - a| < E, resuelves en el miembro del centro:
0 < |0| < E, resuelves el valor absoluto en el miembro del centro
0 < 0 < E que es una desigualdad absurda, ya que 0 no puede ser estrictamente menor que 0 como expresa la primera desigualdad.
Por lo tanto, ya sabemos que a no pertenece al conjunto solución, luego, podemos estudiar la desigualdad doble:
0 <= |x - a| < E, observa que la primera desigualdad se cumple para todo x perteneciente a R, por lo que podemos escribir:
|x - a| < E, luego por propiedades del valor absoluto con las desigualdades (revisa tus apuntes de clase):
- E < x - a < E, luego sumamos a en todos los miembros y cancelamos términos opuestos en el miembro del centro:
- E + a < x < E + a.
Por lo tanto, el conjunto solución queda:
S = { x perteneciente a R: - E + a < x < E + a, con x distinto de a } = (- E + a , E + a) - {a} = (- E + a , a) u (a , E + a).
Espero haberte ayudado.
-
Daniel Pineda
el 1/10/16hola unicoos, quisiera que me dierais una demostración de la desigualdad de Cauchy-Schwarz. He visto algunas relacionadas con una parábola la cual no entiendo muy bien. Desearía una alternativa o si no hay más, explicada lo más detalladamente posible. Gracias de antemano ¡¡
-
Gaussiano
el 1/10/16Hoola!¿por qué la integral de esta función es -ln /3+cos (x)/+ C?
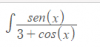yo la separé sen (x)/3 + sen (x)/cos (x) y iba a integrar por separado, pero no acabo de entender la solución de Symbolab. Gracias
Antonio Silvio Palmitano
el 1/10/16¡Cuidado! No puedes distribuir cuando tienes sumas o restas en el denominador.
Para resolver, puedes aplicar la sustitución (cambio de variable)
w = 3 + cosx, de donde tienes: dw = - senx*dx, y luego: - dw = senx*dx, luego sustituyes y queda:
I = Integral ( - dw / w ) = - Integral (1/w)*dw = - ln|w| + C = - ln|3 + cosx| + C.
Espero haberte ayudado.
-
Joaquin Martinez
el 1/10/16hola me ayudais con este problema de razon de cambio
Antonio Silvio Palmitano
el 1/10/16Debes emplear la expresión del área del triángulo, como función de la longitud x y del ángulo comprendido entre los lados con longitudes iguales (indicamos theta con T):
A = (1/2) * x^2 * senT (observa que la expresión es un producto, con x función de t, y T función de t) derivamos (observa que debemos aplicar la regla de la cadena para derivar x^2 y para derivar senT):
A ' = (1/2) * 2x * x ' * senT + (1/2) * x^2 * cosT * T '
Luego tenemos:
x = 6, T = pi/4, x ' = + 1/2 (x está creciendo), T ' = + pi/90 (T está creciendo), reemplazamos y queda:
A ' = (1/2) * 2*6 * (+1/2) * sen(pi/4) + (1/2) * 6^2 * cos(pi/4) * (+pi/90) =
= 3 * V(2)/2 + (pi/15 * V(2)/2 = (3 + pi/15)*V(2)/2.
Espero haberte ayudado.
-
Wayner
el 1/10/16Hola unicoos, me pueden ayudar en este ejercicio de Relaciones trigonometricas?. La respuesta dep ejercicio es: 5 RAIZ 6/24. Creo que lo que me falta no es mucha para llegar a la respuesta...
Antonio Silvio Palmitano
el 1/10/16Observa que en el segundo cuadrante (entre pi/2 y pi) la cotangente toma valores negativos. Puedes emplear la identidad trigonométrica:
(cotgA)^2 = (cosA)^2 / ( 1 - (cosA)^2 ) = reemplazas y resuelves cuadrados
= (25/121) / (1 - 25/121) = (25/121) / (96/121) = simplificamos:
= 25/96 = 25 / (3*32) = multiplicamos y dividimos por 6:
= 25* 6 / (3*3*32*2) = operamos en el denominador:
= 25*6 / (9*64).
Luego extraemos raíz cuadrada (observa que la podemos distribuir entre los factores del numerador y del denominador:
cotgA = - 5*V(6) / (3*8) = - 5*V(6)/24.
Espero habete ayudado.
Wayner
el 1/10/16 -
Gaussiano
el 1/10/16Hoola! He intentado hacer esta integral por partes, pero no me sale. Llamé "u" a cos (2x^2+3) y dv a 2x, creo que hay una manera más fácil de resolverla pero no se me ocurreo ninguna idea. Gracias
Antonio Silvio Palmitano
el 1/10/16Debes plantear la sustitución (cambio de variable):
w = 2x^2 + 3. de donde tienes: dw = 4x*dx, y luego: (1/2)dw = 2xdx, luego sustituyes y la integral queda:
I = Integral cosw*(1/2)dw = (1/2)senw + C = (1/2)sen(2x^2 + 3) + C.
Observa que habías ensayado el método de las partes y se complicó, por lo tanto no olvides que cuando tienes una composición de funciones como en este caso, una opción puede ser el método de sustitución.
Espero haberte ayudado.
