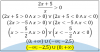-
claudia nuñez ramirez
el 2/10/16
me pueden ayudar por fis, ya es tercera vez que publico el ejercicio y nada, veo que a todos les van respondiendo y a mi no, POR FAVOR , es para una evaluación que sera calificada :'C
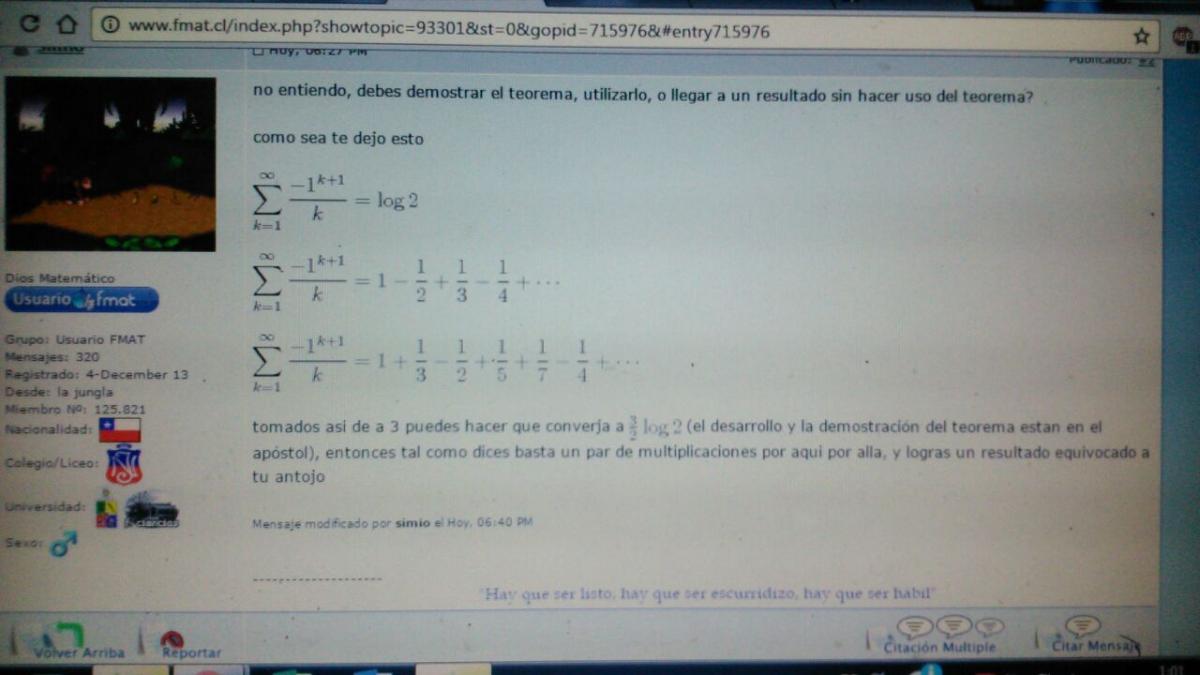
necesito determinar una serie (condicionalmente convergente) que al reordenarla converja a cualquier rut sin el digito verificador (en este caso el valor 19368390) usando el siguiente teorema
COMO AYUDA en el foro fmat meenviaron esto
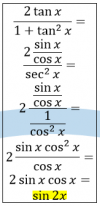
EL TEMA ES QUE NO ENCUENTRO LA SERIE :( , POR FAVOR ANOCHE NO DORMÍ BUSCÁNDOLA y hoy estoy en la misma :c
algún unicoos?? desde ya muy agradecida, si alguien se toma el tiempo y me ayuda ;)
-
Matías
el 2/10/16
Alguien me podría demostrar el ejercicio 3 mediante un dibujo?
David
el 3/10/16Solo la 2 es verdadera... Basta con que dibujes una funcion continua en un intervalo cualquiera (a,b) y le asignes a esos dos valores de "x" el mismo valor de "y"...
Teorema de ROLLE
Teniendo en cuenta que f(a) y f(b) serán amnos máximos de esa función, no puede haber ningun valor de "y" que los supere , por tanto la función deberá decrecer a partir de "a" hasta un determinado valor de x (que llamaremos "c") y luego empezar a crecer hasta llegar a "b"... Eso obliga a que ese valor de "c" sea un minimo... Tiene que ver además, con el teorema de Rolle... -
yanina soledad pineda
el 2/10/16¿como resuelvo este cociente de inecuacion 2x+5/x>0?me gustaria saber cuanto les llevaria darme una respuesta.gracias.
Jorge Labra Canales
el 2/10/16la inecuación es 2*x+(5/x)>0 cierto?
de ser así al sumar nos queda (((2*x^2)+5)/x)>0
podemos ver que el numerador siempre será positivo para cualquier valor que elijamos para la variable "x". Por otro lado, el denominador debe cumplir dos condiciones:
1) no puedo ser cero (5/0 es indefinido)
2) tiene que ser positivo
por ende la solución de esta inecuación es x>0.
Espero haberte ayudado.
Saludos!
-
yanina soledad pineda
el 2/10/16 -
Miguel Ángel Lizama Zavaleta
el 1/10/16¿ De cuántas maneras se pueden acomodar 7 libros en un estante?
a) 3 libros determinados deben estar juntos.
b) 2 libros determinados deben de ocupar los extremos.
son técnicas de conteo de probabilidad pero no estoy totalmente seguro de las respuestas que yo tengo, si alguien me ayuda u orienta estaría muy bien.
Antonio Silvio Palmitano
el 2/10/16Entendemos que los siete libros son distinguibles unos de otros.
1) Permutaciones de 7 elementos: 7! = 5040.
2)
a) Observa que los libros determinados pueden ocupar los lugares: 123, 234, 345, 456, 567, por lo que tenemos cinco opciones para ubicarlos.
b) Una vez que los ubicamos, ordenamos los libros determinados: permutaciones de 3 elementos: 3! = 6.
c) Ordenamos los demás libros en los cuatro lugares disponibles para ellos: permutaciones de 4 elementos: 4! = 24.
Luego, la cantidad total de maneras (principio de multiplicación): N = 5*6*24 = 720.
3)
a) Ordenamos los libros determinados: permutaciones de 2 elementos: 2! = 2
b) Ordenamos los demás libros en los cinco lugares disponibles: permutaciones de 5 elementos: 5! = 120.
Luego, la cantidad total d maneras (principio de multiplicación): M = 2*120 = 240.
Espero haberte ayudado.
-
Keith Caballero Rodriguez
el 1/10/16Me pueden ayudar con este problema que no lo he podido resolver hace una semana.
-
Wayner
el 1/10/16 -
Agus Strano
el 1/10/16Hola unicoos, tengo un ejercicio que no puedo resolver de funciones trigonometricas:
Encontrar todos los X ∈ [ - π ; π ] tales que: sen (x) = -√3/2
¿como se en que cuadrante esta, para poder descubrir que soluciones posibles tiene? -
The punk
el 1/10/16 -
Pablo Reyes
el 1/10/16
