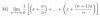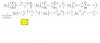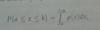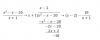hola! Me podrían ayudar con este ejercicio? Graaciaas 

Hola ,  podría alguien ayudarme a resolver  dos ejercicios de mi tarea de Cálculo por favor. A qué se refiere x que minimiza la función? Gracias

Alguien me ayuda con este ejercicio, estaba viendo una parte de la solucion y no la comprendo mas que nada al empezar si alguien me da una mano, y me ayuda a decir porque se da (lo marcado en negrita y subrayado)

Sean a,b∈Ra,b∈R tales que 0<a<10<a<1 y b>0.b>0. Demostrar que la ecuación x=a sen x+bx=a sen x+b tiene al menos una raíz positiva menor o igual que a+b...

Parte sol: La función f(x)=x−a sen x−b es continua en R, por tanto lo es en [0,a+b].

esta bien si considero el pto ( 0,5) como el F Y F`, luego se que la distancia focal ( lease C ) c= 5,

tambien se que la suma de los dos focos es 10 y la diferencia es 6, con una simple ecuacion y despeje consigo el valor de a: 10 + a  = 6 eso me da a = 4 

ahora simplemente me meto en la ecuacion c^2=a^2+b^2------->  25= 16 +b^2-------> b= 3 

OTRO METODO SERÍA la distancia entre dos puntos pero creo que es más largo, si alguien me lo puede decir se lo agradezco 

Hola...

Seria posible que me colaboran con esta pregunta de estadística.

La ecuación A.15 es: 

y la ecuación A.20 es:

Donde "exp" es la función exponencial en base e, μ es el valor promedio y σ es la desviación estándar

De antemano muchas gracias

Alguien me puede ayudar con estas derivadas parciales

Calcular dw/dx, dw/dy, dw/dz 
en xyz + xzw + w^2 - yzw = 4

Sean A, B, C tres matrices de orden n tales que (2A + In)B = B + ACA. Indique bajo qué
condiciones se puede despejar C y hágalo. Simplifique al máximo el resultado.

¿He despejado bien la C? ¿Cuáles serían las condiciones?

Estaba haciendo el ejercicio, y llegué a -1=1

Si alguien me dice qué hice mal por favor.

Necesito dividir los siguientes polinomios de forma clásica y no me da el mismo resultado que por Ruffini. 

(x² -x-20) / (x+1)

 demostrar (A\B)u(B\A) = (AuB) \ (A(interseccion)B).

\= diferecencia de conjuntos