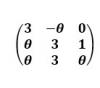-
Una consulta, el vector nulo (0,0,0) es perpendicular y paralelo a cualquier vector en R3 o no se considera?
Gracias.
-
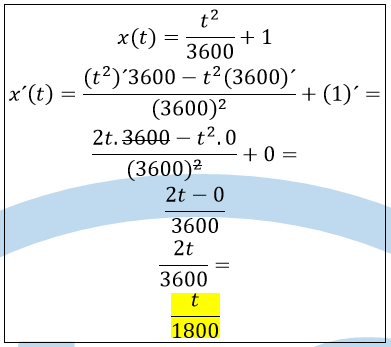
Ayuda con ejercicio de derivadas parciales porfavor, lo que he resuelto es solo el inciso a pero quisiera saber si esta bien hecho...

-
Hola amigos de unicoos necesito su ayuda, yo estoy estudiando numeros complejos y quiero hacer ejercicio para afirmar la teoria ustedes podrian pasarme algunos ejercicios
-
Buenas tardes, necesito sacarme una duda con este ejercicio de cónicas. Dice así: Encontrar en el sistema (O,XY) la ecuación general de la cónica de un elipse que posee centro en el origen de coordenadas, eje mayor sobre la recta de ecuación 2x-y=0, distancia entre los vértices principales igual a 10 y un vértice en A'=(2,-1).
Pude sacar la ecuacion en el sistema (O,X'Y') pero no se como pasarlo al.otro sistema. Agradecería la ayuda. Gracias.


Antonio Silvio Palmitano
el 24/9/16Observa que la ecuación explícita de la recta que contiene al eje mayor es: y = 2x.
Por lo tanto, la ecuación explícita de la recta que contiene al eje menor es: x = -2y.
Recuerda que son perpendiculares, y que se cortan en el origen de coordenadas, y que la recta que contiene al semieje mayor pasa por los focos y por los vértices principales:
Luego vayamos al vértice que tienes en el enunciado: A'(2,-1): puedes verificar que pertenece al la segunda recta, por lo tanto el semieje menor podemos calcularlo:
b = distancia (0,A') = V(5).
Luego, planteamos las coordenadas de los vértices principales: A1(p,-2p) y A2(-p,-2p), puedes verificar que pertenecen a la primera recta, luego, como conocemos la distancia entre ellos planteamos para el semieje mayor:
a = (1/2)*distancia(A1,A2) = 2V(5)p = 10, de donde despejamos y tenemos p = V(5) (observa que ya tienes las coordenadas de los vértices principales), y el semieje mayor queda: a = (1/2)*10 = 5.
Hasta el momento tenemos:
semieje mayor: a = 5, semieje menor: b = V(5), y con la relación entre semiejes podemos tener la semidistancia focal:
c = V(a^2 - b^2) = V(25 - 5) = V(20) = 2V(5).
Luego, los focos tendrán coordenadas: F1(q,2q) y F2(-q,-2q), luego planteamos:
distncia(F1,F2) = 2c, aplicamos la expresión de la distancia entre dos puntos y queda:
V(20)q = 2V(20), de donde tenemos: q = 2, y las coordenadas de los focos: F1(2,4) y F2(-2,-4).
Luego, puedes plantear la definición de elipse (recuerda que P(x,y) es un punto genérico de la elipse):
distancia(F1,P) + dist(f2,P) = 2a, desarrollamos, y queda:
V( (x-2)^2 + (y-4)^2 ) + V( (x+2)^2 + (y+4)^2 ) = 10.
De aquí en más, es cuestión de operar tal cuál como seguramente has hecho en clase para establecer la ecuación de una elipse a partir de su definición.
Espero haberte ayudado.
-
Hola, no puedo despejar las X de un lado y las Y del otro lado de la igualdad en un ejercicio de EDO 1° orden. Agradecería su ayuda.
- y ' - 3y/x = x4 ex
- y(1) = 2


Antonio Silvio Palmitano
el 24/9/16Para este tipo de ecuaciones diferenciales (lineales, de primer grado y de primer orden), cuya forma general es: y ' + P(x)*y = Q(x), vamos por pasos:
En este ejercicio tenemos: P(x) = -3/x, y Q(x) = x4 * e^x.
1) Calculamos: A(x) = Integral ( P(x) * dx ) = Integral ( - 3/x)*dx = - 3*lnx = ln(x^(-3)), y su opuesta: - A(x) = - ln(x^(-3)) = ln( 1 / x^(-3) ) = ln(x^3).
Planteamos la solución general:
y = e^( - A(x) ) * ( Integral ( e^A(x) * Q(x) * dx ) + C ), reemplazamos, resolvemos composiciones entre exponencial y logaritmo natural y queda:
y = x^3 * ( Integral ( x^(-3) * x^4 * e^x * dx ) + C ), resolvemos potencias en el argumento de la integral y queda:
y = x^3 * ( Integral ( x * e^x * dx ) + C ), resolvemos la integral ( por partes, como seguramente has visto en clase) y queda:
y = x^3 * ( x*e^x - e^x + C ), distribuimos, resolvemos potencias en el primer término y queda.
y = x^4 * e^x - x^3 * e^x + C * x^3, que es la solución general (o familia de soluciones) de la ecuación diferencial.
Por último, empleamos la condición y(1) = 2 para evaluar la expresión y determinar el valor de la constante para la solución particular. Reemplazamos, resolvemos y queda:
2 = e - e + C, luego cancelamos términos opuestos a la derecha y tenemos: 2 = C.
Por lo tanto, la solución particular será:
y = x^4 * e^x - x^3 * e^x + 2* x^3.
Espero haberte ayudado.
-
Hola. Se que es sabado a última hora, pero a ver si me podrian ayudar con una duda:
En el ejercicio 11 de la foto el apartado C no lo entiendo muy bien, todo lo demás lo tengo echo, pero llegado a ese apartado, no se como continuar.


Antonius Benedictus
el 24/9/16Cuando transformas una variable estadística multiplicando todos los valores por una constante k:
La media aritmética queda multiplicada por dicha constente.
La varianza queda multiplicada por el cuadrado de dicha constante.
La desviación típica queda multiplicada por el valor absoluto de dicha constante.
El coeficiente de variación, por tanto, permanece inalterable o cambia de signo (si k<0).