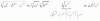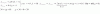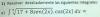-
Pilar Elvira
el 25/9/16Hola!! He buscado y no encontré un video sobre las propiedades de las operaciones respecto a los números reales.Tengo dudas en este apartado del tema :\
Gracias.
-
Gaussiano
el 25/9/16 -
Lsslie
el 25/9/16Hola! Me podéis con el apartado b) porfas? Es un limite cuando x tiende a + infinito. Gracias!
-
Iris Lopez
el 25/9/16 -
Anna
el 25/9/16Hola, podrían resolverme una duda? En las ecuaciones racionales, como se halla el mínimo común múltiplo? Gracias
Antonio Silvio Palmitano
el 25/9/16Si te refieres al mínimo común denominador, éste se plantea como el mínimo común múltiplo entre los polinomios denominadores, y lo obtienes por medio de los pasos siguientes:
1°) Factorizas los polinomios denominadores.
2°) Planteas al minimo común múltiplo como el producto de los factores comunes a todos o a algunos con su mayor exponente, junto a los factores no comunes.
3°) Agregas como coeficiente al mínimo común múltiplo entre todos los coeficientes de los denominadores.
Por ejemplo, si debes plantear el mínimo común divisor entre tres expresiones fraccionarias, cuyos denominadores son:
A(x) = x^3 - x^2 = factorizas y queda: = x^2 * (x - 1)
B(x) = 6x^2 - 6 = factorizas y queda: = 6*(x2 - 1) = 6*(x + 1)*(x - 1).
C(x) = 15x^3 - 30x^2 + 15x = factorizas y queda: = 15x*(x^2 - 2x +1) = 15x*(x - 1)^2.
Luego, el mínimo común múltiplo entre los tres denominadores (que será nuestro mínimo común denominador) queda:
mcm[A,B,C] = 30 * x^2 * (x - 1)^2 * (x + 1).
Espero haberte ayudado.
-
Bet
el 25/9/16Buenos días como se puede resolver la letra B?
Si es posible indicar resultado (no estoy seguro de que me tiene que dar)
Gracias de antemano
Antonio Silvio Palmitano
el 25/9/16Comencemos por denominar:
radio de la base del cono (R), su altura (H) y su generatriz (G): G = V(R^2 + H^2);
radio de la base del cilindro (r) y su altura (h).
Observa que las áreas laterales quedan (llamamos A1 al área total del cilindro, que tiene dos bases y cara lateral, y A2 al área total del cono, que tiene una base y cara lateral):
A1 = 2pi * r^2 + 2pi*r*h = reemplazamos datos = 2pi*8^2 + 2pi*8*10 = 128pi + 160pi = 288pi (expresada en centímetros cuadrados).
A2 = pi*R^2 + pi*R*G = reemplazamos datos: = pi*8^2 + pi*8*G = 64pi + 8pi*G.
Luego, según la consigna del inciso (b) igualamos y queda la ecuación:
64pi + 8pi*G = 288pi, dividimos por 8pi en todos los términos, simplificamos y queda:
8 + G = 36, de donde despejamos, resolvemos y llegamos a:
G = 28 (expresada en centímetros).
Luego, si preguntan por la altura del cono, puedes apelar a la relación pitagórica entre el radio de la base del cono (R), su altura (H) y su generatriz (G): G = V(R^2 + H^2).
Espero haberte ayudado.
-
Cristian Jiménez Corona
el 25/9/16Cómo represento el rango si "y" sólo toma múltiplos de 3?
Antonio Silvio Palmitano
el 25/9/16 -
Rodrigo Velázquez
el 25/9/16Buena noche, podrían ayudarme de favor con este problema de optimización?
Elaborar una pieza de cierto producto le cuesta a una empresa L unidades de capital para mano de obra & K unidades de capital para materia prima. Bajo estas condiciones, la empresa puede elaborar P unidades de su producto, donde: 𝑃(𝐿, 𝐾) = 50𝐿2/3𝐾1/3
Si cada unidad de producto le cuesta a la empresa 100 dólares en mano de obra y 300 dólares de materia prima, y si la empresa dispone de una suma de 45 mil dólares para su producción, determina las unidades de mano de obra y de materia prima que permiten maximizar la producción.
El resultado debe de dar 𝐿 = 300 & 𝐾 = 50.
Se que mi restricción es 100L +300K= 45000, pero me he perdido en la parte de derivación y sustitución en las ecuaciones.
gracias.
-
Nicolas Ferryra
el 25/9/16 -
Karla Pamela Saavedra Changanaqui
el 25/9/16Buenas noches,porfavor quiero saber como seria la resolucion de estas dos integrales trigonometricas que me resultan dificultosas al resolverlos, son para practicar para un examen.De antemano le agradesco su ayuda.
Axel Morales Piñón.
el 25/9/16
Axel Morales Piñón.
el 25/9/16
