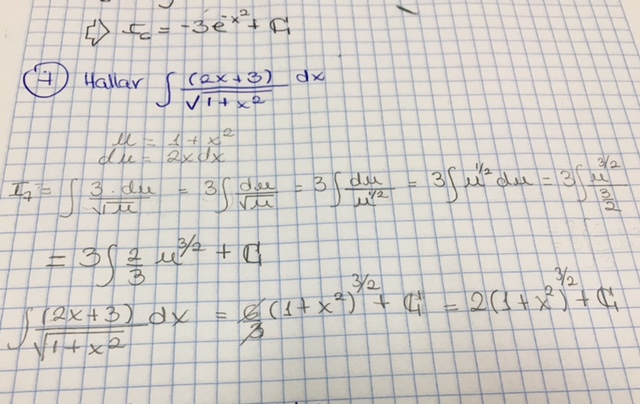-
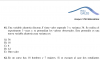
Burnas unicoos, supe como resolver estos ejercicios (los revise y para mi estan buenos) pero como los resuelvo no me da el resultado que me dieron. En el primero la respuesta que me dan es: 27 y a mi me dio x=13. Y el segundo la opcion correcta es la a) 25 raiz de cinco y a mi me dio x=5/2. Podrian ayudarme en encontrar las soluciones para llegar a esas soluciones que me dan y verificar si los ejercicios que hice estan bien. Muchas gracias.



-
Hola¡¡¡¡¡ disculpen este ejercicio me dicen que esta mal ; ayúdenme por favor:

Halla los valores de h(x)=tg(x) -2csc(2x) sabiendo que: -3π⁄4 < x ≤ -π⁄6 .


David
el 20/9/16Te confundiste nada mas empezar con la csc(2x). La susituiste por cosecx...
Yo habría hecho... tanx - 2/sen(2x)=senx/cosx -2/(2.senx.cosx)=senx/cosx -1/(senx.cosx).. Pasando a comun denominador... sen²x/(senx.cosx) -1/(senx.cosx) = (sen²x-1)/(senx.cosx)
Como cos²x=1-sen²x..... sen²x-1=-cos²x....... -cos²x=(senx.cosx)=-cosx/senx=-cotanx
Te dió lo mismo por PURA CASUALIDAD....
A partir de ahí, no sabría que decirte porque el enunciado no tiene sentido (no es una ecuacion ni una identidad)...
¿que te piden que hagas con h(x)? ¿averiguar cuando es 0? ¿estudiar su signo?... -
Hola unicoos, debo resolver esta integral y llego hasta esa sustitución y no sé cómo continuar, desde ya les agradezco en lo que puedan ayudarme.



Antonio Silvio Palmitano
el 20/9/16De acuerdo con el colega Peter. Puedes emplear la sustitución (cambio de variable):
u = 2*tanw (*)
de donde tienes:
dw = ( 2 / (cosw)^2 )*dw
y también tienes:
4 + u^2 = 4 + 4*(tanw)^2 = 4*( 1 + (tanw)^2 ) = por identidad tirgonométrica = 4*( 1 / (cosw)^2 ) = 4 / (cosw)^2
luego, el denominador queda:
( 4 / (cosw)^2 ) ^(3/2) = 8/(cosw)^3.
Luego, sustituyes en la integral y queda:
I = Integral ( cosw)^3 / 8 )*( 2 / (cosw)^2 )*dw = I (1/4)*Integral cosw*dw = (1/4)*senw + C.
Luego, a partir de la ecuación indicada (*) tienes:
w = arctan(u/2)
y a partir de la sustitución que has propuesto en tu trabajo:
u = x - 1
Luego sustituyes, y tienes la expresión en función de la variable original x.
Espero haberte ayudado.
-
Buenas amigos de unicoos podrian ayudarme a resolver esta ecuacion con esta solucion explicita por favor
dy/dt+20y=24: y=6/5-6/5e^-20t


David
el 20/9/16Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. Lo siento de corazón… Espero lo entiendas
Es posible te ayuden los vídeos de "ecuaciones diferenciales" ... Ecuaciones diferenciales

Antonio Silvio Palmitano
el 20/9/16Observa que puedes separar variables, haces un pasaje de término y queda:
dy/dt = 24 - 20y, luego extraes factor común a la derecha y queda:
dy/dt = 4*(6 - 5y), luego haces pasajes de factor como divisor, y de divisor como factor y queda:
dy / (6 - 5y) = 4*dt, luego integras miembro a miembro (a la izquierda por medio de la sustitución (cambio de variable): w = 6 - 5y) y queda:
(-1/5)*ln|6 - 5y| = 4t + C, multiplicamos en ambos miembros por -5, expresamos -5C como k y queda:
ln|6 - 5y| = -20t +k, componemos con la función inversa del logaritmo natural y queda:
6 - 5y = e^( -20^t + k ), aplicamos propiedad del producto de potencias con bases iguales, expresamos e^k como K y queda:
6 - 5y = K*e^(-20t), luego hacemos pasaje de término y queda.
-5y = -6 + K*e^(-20t, por último multiplicamos en todos los términos por -1/5, expresamos (1/5)K como A y queda:
y = 6/5y = 6/5 - A*e^(-20t), que es la solución general de la ecuación diferencial.
Observa que en tu respuesta, tienes el caso particular para A = 6/5, que corresponde a la condición y(0) = 0.
Espero haberte ayudado.
-
- Alguien me ayuda con este ejercicio de COMPLEJOS, como indica pide el centro de giro en forma binomica y el angulo de giro.

- Intente aplicar la formula f(z) = az +b
- donde a= not polar de complejo
- b= zo (1-a)
Ayuda pliss


Antonio Silvio Palmitano
el 20/9/16Observa que el centro de giro es un punto fijo para la función lineal, por lo que planteamos:
f(z) = z, reemplazamos y queda la ecuación:
iz + 2 - 4i = z, hacemos pasajes de términos extraemos factor común a la izquierda y queda:
(-1+i)z = -2+4i, hacemos pasaje de factor como divisor y queda:
z = (-2+4i)/(-1+i), luego multiplicamos al numerador y al denominador por (-1-i), resolvemos y queda:
z = (6-2i)/2, distribuimos el denominador, simplificamos y tenemos:
z = 3-i, que es el punto fijo para esta función lineal, o centro de giro.
Luego, el coeficiente del término de primer grado en la expresión de la función es el que determina dilatación o contracción, y el ángulo de giro.
En este caso, tenemos que el coeficiente es: a = i, cuyo módulo (o norma) es |a| = 1, y cuyo argumento es t = pi/2.
Observa que el módulo es igual a 1, por lo que no tenemos dilatación ni contracción, y que el ángulo de giro es pi/2 tal como indica el argumento.
Espero haberte ayudado.
- Alguien me ayuda con este ejercicio de COMPLEJOS, como indica pide el centro de giro en forma binomica y el angulo de giro.
-
Buenas, me podrian ayudar a determinar para que valores de x perteneciente a los numeros reales se tiene que:
x ^ (1/2) = e * log x
Un saludo.


David
el 20/9/16Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. Lo siento de corazón… Espero lo entiendas
La solucion, no obstante, la tienes aquí... http://www.wolframalpha.com/widgets/view.jsp?id=148b5e39237cc2678c3cab6b524c3484 -
Hola buenas, mire llevo 1 hora con este ejercicio y ni si quiera se cómo plantearlo. Dice así
Sea f una función continua en R tal que: -ex menor o igual que f(x) menor igual que e-x
para todo x perteneciente a los números reales
Entonces la pregunta es: ¿Existe un punto a perteneciente a R tal que f(a) =a ?


Antonio Silvio Palmitano
el 20/9/16Un posible camino:
Podemos restar x en los tres términos, y la doble desigualdad queda:
-e^x - x <= f(x) - x <= e^(-x) - x
observa que en los tres miembros tenemos expresiones que corresponden a funciones continuas.
Para la función de la izquierda, tenemos:
A(x) = - e^x - x, A(-1) = 0,63 (aproximadamente) > 0, A(1) = -3,71 (aproximadamente) < 0
Observa que la función A pasa de tomar un valor positivo para x = -1, a tomar uno negativo para x = 1.
Para la función de la derecha tenemos:
B(x) = e^(-x) - x, B(-1) = 3,71 (aproximadamente) > 0, B(1) = -0,63 (aproximadamente) < 0.
Observa que la función B pasa de tomar un valor positivo para x = -1, a tomar uno negativo para x = 1
Luego, como la función C(x) = f(x) - x está comprendida entre las funciones A(x) y B(x), tenemos que:
la función C toma un valor positivo para x =-1, tal que: 0,63 <= C(-1) <= 3,71,
la función C toma un valor negativo par x = 1, tal que: -3,71 <= C(1) <= -0,63.
Por lo tanto, por ser C una función continua que cambia de signo en el intervalo [-1,1], tenemos que exista a pertenceciente al intervalo (-1,1) tal que C(a) = 0, desarrollamos la expresión de la izquierda y queda:
f(a) -a = 0
hacemos pasaje de término y llegamos finalmente a:
f(a) = a.
Espero haberte ayudado.