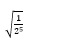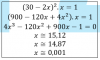-
hola unicoos, queria saber si me ayudan con este ejercicio. El punto C (3,-1) es el centro de una circunferencia cuya intersección con la recta L: 2X-5Y+18=0 Genera una cuerda de longitud, igual a 6u. Hallar la ecuación de la circunferencia:
-
Hoola! Estoy repasando vectores No recuerdo mucho la fórmula que hay que aplicar en el punto 5 y el punto 6, gracias.



Antonio Silvio Palmitano
el 21/9/165) Lo haces en dos pasos:
a) Calculas el vector w = A x B, que por propiedad del producto vectorial será un vector perpendicular a A y también a B
b) Divides a todas las componentes de w por el módulo de w, y obtendrás el vector unitario.
6)
El módulo de A queda: |A| = V(3^2 + 4^2) = V(25) = 5.
Luego observa que el vector tiene sus dos componentes positivas, por lo que su ángulo de inclinación con respecto al semieje OX positivo será menor que p/2, por lo que planteamos su tangente: tan(a) = 4/3, componemos con la función inversa de la tangente y queda: a = 53,13° = (53,13/180)*pi = 0,30*pi radianes (aproximadamente).
Por lo tanto, las componentes polares para el vector A son: |A| = 5, a = 0,3*pi radianes.
Espero haberte ayudado.
-
- Buenas noches! Puede que la solución no sea correcta, solo me gustaría saber donde puedo encontrar la explicación de como solucionar ese tipo de problema, osea a la raíz cuadrada de la fracción elevada al quinto. He estado buscando en Radicales y no encuentro la explicación de que hacer con esa potencia.. Alguna sugerencia?
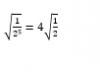


Antonio Silvio Palmitano
el 21/9/16Observa que:
1/2^5 = 1^5/2^5 = (1/2)^5 = (1/2)^4 * (1/2),
luego, cuando tomas su raíz cuadrada queda:
V( 1/2^5) = V( (1/2)^4 * (1/2) ) = distribuimos la raíz entre los factores = V( (1/2)^4 ) * V(1/2) = simplificamos en el primer factor = (1/2)^2 * (1/2) = (1/4) * V(1/2).
Observa que nos ha quedado, igualando el último miembro con el primero de la cadena de igualdades:
(1/4) * V(1/2) = V( 1/2^5)
Observa que la igualdad que presenta tu primera foto no coincide, por lo que deberás preguntar a tus docentes si no se trata de un error de impresión en tu apunte.
El procedimiento que hemos empleado consiste en expresar al argumento de la raíz como producto de factores, en este caso uno de ellos con potencia cuyo exponente es simplificable con el índice de la raíz.
Espero haberte ayudado.
- Buenas noches! Puede que la solución no sea correcta, solo me gustaría saber donde puedo encontrar la explicación de como solucionar ese tipo de problema, osea a la raíz cuadrada de la fracción elevada al quinto. He estado buscando en Radicales y no encuentro la explicación de que hacer con esa potencia.. Alguna sugerencia?
-
Buenas que hay ? Vengo de nuevo a pedir vuestra ayuda. Tengo que hacer un mapa conceptual con los siguientes conceptos: Limite, continuidad, derivabilidad, acotación, y crecimiento. Me gustaria saber de qué manera se relacionan estos conceptos. Muchas gracias por vuestra ayuda
-
Buenas! Acabo de entrar a químicas y hace años que no tocaba las matemáticas que se dan en bachiller (de hecho, en 2º de Bach no me las cogí). En matemáticas estamos dando un repaso general de conceptos de bachiller y no me acuerdo de nada. Quisiera tener algunos conceptos claros antes de pedir alguna tutoría al profesor porque con lo poco que recuerdo el pobre se tendría que estar horas explicándome...
Bien, el ejercicio es sencillo. Hallar el dominio, el rango y representar gráficamente. Me surge la duda en la función f(x) = Raíz 5 - x^2. Tengo anotado de las correcciones que el dominio sería +/- Raíz 5. Sé que es muy sencillo, pero no sé el motivo de por qué es ese el dominio (al igual que es el rango). Una ayuda, por favor. Gracias de antemano


Antonio Silvio Palmitano
el 20/9/16Te recomiendo recorras los vídeos, porque este tema está desarrollado en ellos. Vamos con la expresión de tu función:
f(x) = V(5 - x^2)
La condición para las raíces cuadradas (o de índice par en general) es que su argumento debe ser positivo, por lo que planteamos:
5 - x^2 >= 0, hacemos pasaje de término y queda
- x^2 >= -5, multiplicamos en ambos miembros por -1 (recuerda que cambia el sentido de la desigualdad) y queda:
x^2 <= 5, luego hacemos pasaje de potencia par como raíz (recuerda que nos queda valor absoluto de su argumento) y queda:
|x| <= V(5), luego, por propiedad del valor absoluto llegamos a:
- V(5) <=x <= V(5), por lo que concluimos que el dominio de la función es el conjunto de números reales comprendido entre - V(5) y V(5), comprendiendo a ambos:
D = [ - V(5),V(5)] = {x perteneciente a R: _ V(5) <= x <= V(5) }.
Recuerda la definición de valor absoluto:
|x| = x, si x >= 0, y |x| = - x, si x < 0.
Y dos propiedades importantes (a es un número real positivo):
|x| <= a es equivalente a - a <= x <= a (que es la que hemos aplicado en el ejercicio);
|x| >= a, que nos lleva a dos opciones: x <= a, o x >= a.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 20/9/16Puedes plantear:
y: cantidad de alumnos que conocen su nota, transcurrido un tiempo t desde la publicación;
x: cantidad de alumnos que no conocen su nota, transcurrido un tiempo t desde la publicación;
t: tiempo transcurrido desde la publicación, medido en horas;
K: constante de proporcionalidad.
Luego, tenemos la condición: x + y = 50, de donde despejamos: x = 50 - y (*), con x e y pertenecientes al conjunto de los números naturales.
Luego planteamos:
y ' = K*t*x, luego sustituimos según la ecuación señalada (*) y queda:
y ' = K*t(50 - y), luego expresamos a la derivada (razón de cambio instantánea) como cociente entre diferenciales:
dy/dt = K*t*(50 - y), hacemos pasajes de divisores y factores para separar variables y queda:
dy/(50 - y) = K*t*dt, luego integramos miembro a miembro (para integrar a la izquierda apelamos a la sustitución: w = 50 - y):
- ln|50 - y| = K*(1/2)*t^2 + C (*).
Luego, para determinar los valores de las constantes K y C tenemos las condiciones:
a) y(0) = 0 (al inicio ningún estudiante conoce su nota), reemplazamos y queda: - ln(50) = C (**)
b) y(1) = 25 (transcurrida una hora, la mitad de la clase conoce sus notas):, reemplazamos y queda:
- ln(25) = K*(1/2) - ln(50), hacemos pasaje de término y queda:
ln(50) - ln(25) = K*(1/2), aplicamos propiedad del logaritmo de un cociente y queda:
ln(50/25) = K*(1/2), resolvemos el argumento del logaritmo, multiplicamos por 2 en ambos miembros y queda:
2*ln(2) = K (***).
Luego, sustituimos las expresiones señaladas (**) (***) de las constantes C y K en la ecuación señalada (*) y queda:
- ln|50 - y| =2*ln(2)*(1/2)*t^2 - ln(50), resolvemos coeficientes en el primer término de la derecha y queda:
- ln|50 - y| =ln(2)*t^2 - ln(50).
Por último, evaluamos para t = 2 y queda:
- ln|50 - y| = ln(2)*2^2 - ln(50), resolvemos la potencia en el primer término de la derecha y queda:
- ln|50 - y| =4*ln(2) - ln(50), aplicamos propiedad del logaritmo de una potencia y resolvemos en el primer término de la derecha:
- ln|50 - y| = ln(16) - ln(50), aplicamos propiedad del logaritmo de un cociente y resolvemos a la derecha:
- ln|50 - y| = ln(8/25), multiplicamos por -1 en ambos miembros y queda:
ln|50 - y| = - ln(8/25), aplicamos propiedad del logaritmo del inverso multiplicativo a la derecha y queda:
ln|50 - y| = ln(25/8), componemos en ambos miembros con la función inversa del logaritmo natural y queda:
50 - y = ln(25/8), luego despejamos y, llegando a:
50 - ln(25/8) = y, resolvemos y tenemos:
y(2) = 50 - 1,139 = 48,86 (aproximadamente),
por lo que concluimos que a las dos horas 48 (o 49) alumnos conocen sus notas.
Espero haberte ayudado.
-
ayudaaaaaaaaaaaaaaaa por favorrrrrrrrrr!!!!!!!!!!!!!!!!!
necesito esta ecuacion
(30-2x)^2 · x = 1


David
el 22/9/16TU DUDA ES DE QUÍMICA Y deberás dejarla en el foro de química.
Te sugiero que antes, eso sí, veas todos los vídeos de esta lección... QUIMICA moles de átomos y moléculas
Y también este... Gases ideales PV=nRT No se trata solo de dejar enunciados...Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. #nosvemosenclase Nos cuentas ¿ok?
-
Hola, me han mandado este ejercicio en clase y no hay manera de resolverlo, a ver si alguien me puede echar una mano :)
x + 2y = z
x^2 - 4y^2 + z^2 = 310
Condición: Que el resultado salga un número entero positivo.


Antonio Silvio Palmitano
el 20/9/16Haces un pasaje de término en la primera ecuación y queda:
2y = z - x, elevas al cuadrado en ambos términos y queda:
4y^2 = (z - x)^2, sustituyes en la segunda ecuación y queda:
x^2 - (z - x)^2 + z^2 = 310, desarrollas el binomio a cuadrado, distribuyes el signo y queda:
x^2 - z^2 + 2xz - x^2 + z^2 = 310, cancelas términos opuestos y queda:
2xz = 310, haces pasaje de factor como divisor, resuelves a la derecha y queda:
xz = 155;
luego sustituyes z a partir de la primera ecuación inicial y queda:
x(x + 2y) = 155, distribuyes y queda:
x^2 + 2xy = 155, sumamos y^2 en ambos miembros y queda:
x^2 + 2xy + y^2 = y^2 + 155, factorizamos a la izquierda y queda:
(x + y)^2 = y^2 + 155.
Luego, investigamos valores de y para que en el segundo miembro quede un cuadrado perfecto, observa que si y = 13 (*), reemplazamos y queda:
(x + 13)^2 = 13^2 + 155, resolvemos a la derecha y queda:
(x + 13)^2 = 324, que nos conduce a dos opciones
1) x + 13 = 18, de donde tenemos: x1 = 5, y al reemplazar y resolver en la primera ecuación inicial queda: z = 5 + 2*13 = 31, por lo que nos queda para verificar en la segunda ecuación si x=5, y = 13, z = 31 es una solución (puedes verificar que es válida).
2) x + 13 = -18, de donde tenemos: x2 = -31, y al reemplazar y resolver en la primera ecuación inicial queda: z =-31 + 2*13 = -5, por lo que nos queda para verificar en la segunda ecuación si x = -31, y = 13, z = -5 es una solución (puedes verificar que es válida).
Espero haberte ayudado.