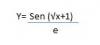Jose lo hice por barrido de intervalos, espero te sea útil

1) Halla la distancia entre P1 y P2... Tu punto Q(x,y,z) que debe cumplir la ecuacion del plano P1,P2,P3 que debes hallar, estará a una distancia igual de P1 y de P2, de donde podrás obtener otras dos ecuaciones. Por ejemplo √[(x-1)²+(y-2)²+(z+1)²] = d(P1,P2)

2a) se trata de hallar la distancia de un punto a una recta

2b) para empezar se trata de que halles la ecuacion de un plano que contiene a R,Q y T...

Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. #nosvemosenclase Nos cuentas ¿ok?

Echa un vistazo a TODOS LOS VÍDEOS DE ESTE TEMA.... 

Te lo corregimos, Demi:

Gracias, me habia equivocado en la redaccion de la pregunta, la inecuacion era en realidad:    |(x+2):(2x-3)|<4  .De todas formas no era lo importante.

Te la damos, Facundo:

Lo primero a tener en cuenta es el dominio de la función y, como es polinómica en este caso, es el conjunto de los números reales. Luego, planteamos su derivada primera y su derivada segunda:

y ' = 6x^2 + 6x - 36

y ' '  = 12x + 6

Luego, planteamos al condición de punto crítico (o singular: posible Máximo, posible Mínimo o posible Inflexión): y ' = 0, sustituimos y queda:

6x^2 + 6x - 36 = 0, observa que podemos dividir por 6 en todos los términos y queda:

x^2 + x - 6 = 0, observa que es una ecuación polinómica cuadrática, cuyas raíces son:

x1 = - 3

x2 = 2

Luego, estudiamos la concavidad de la gráfica en cada uno de los puntos críticos, evaluándolos en la derivada segunda:

Para x1 = - 3 tenemos: y ' ' = 12*(-3) + 6 = -30 < 0, por lo que tenemos que la gráfica es cóncava hacia abajo en el punto y, por lo tanto, presenta un Máximo Local en x1 = -3.

Para x2 = 2 tenemos: y ' ' = 12*2 + 6 = 30 > 0, por lo que tenemos que la gráfica es cóncava hacia arriba en el punto y, por lo tanto, presenta un Mínimo Local en x2 =2.

El procedimiento que hemos empleado es el criterio de la derivada segunda, y puedes verificar a un graficador para corroborar que hemos arribado a conclusiones correctas.

Te recomiendo que mires los vídeos relacionados con estos temas.

Espero haberte ayudado.

Hola Luis!

Las funciones presentarán máximo o mínimos(absolutos o relativos) en los puntos en que su primera derivada sea igual a 0. 

La primera derivada de la función de tu ejercicio es:

y' = 6x^2+6x-36

Como queremos encontrar los puntos en que se hace 0, igualamos a 0

6x^2+6x-36=0

Dividimos por 6 para que se haga más sencilla:

x^2+x-6=0

Y ahora resolvemos esa ecuación de segundo grado. La función puede escribirse como:

(x+3)*(x-2)=0

y por lo tanto la función presentará máximos o mínimos en x=2 y x=-3. Ahora, ¿cómo saber si son máximos o mínimos?

Hay más de un método, pero el que me gusta es estudiar la primera derivada con una tabla que te dejaré a continuación. Lo que se tiene que entender acá es que, la primera derivada al ser la pendiente de la función, si es negativa, significa que la función será decreciente (pendiente negativa=función decreciente) y si la primera derivada es positiva, entonces tenemos una función creciente.

Los movimientos en el plano son isometrías (mantienen las distancias y las formas), por lo que un segmento o un ángulo no se pueden "reducir" (ni "ampliar").

Una recta doble (o invariante) en un movimiento lo sería cuando el vector que lo determina puede ser considerado como vector director de la recta.

Lo primero se explica de este modo:

Si C es un punto entre A y B, ningún movimiento puede transformar AB en BC y, análogamente, si la recta r es interior al ángulo ab, ningún movimiento puede transformar al ángulo ab en bc. 

Lo de lasa rectas dobles aclaralo un poco mas, te puedo decir que:

En una transformación, un punto se llama doble cuando su transformado es él mismo. Una recta es doble si su transformada es ella misma.

Entonces la simetria axial seria la unica que tendria una recta doble?

y si tengo una simetria central de un segmento AB y el punto para la simetria es el punto que divide al segmentos a la mitad, el segmento A´B´ resultante no seria una recta doble?

Es así, Martín:

Te explicamos, Raúl:

Muchísimas gracias Antonio!!

Si has copiado el enunciado completo, observa que el denominador es una constante (e = 2,7182..), si es así comenzamos por analizar que en el numerador tenemos una función compuesta, por lo que debemos aplicar la regla de la cadena y, para simplificar el planteo, escribimos a la raíz del argumento del seno como potencia con exponente fraccionario y queda:

y = sen( x^(1/2) + 1) / e (según has escrito, se entiende que el argumento está expresado en dos términos).

Luego derivamos en numerador solamente, ya que el denominador es constante y queda

y ' = cos( x^(1/2) + 1 ) * (1/2)x^(-1/2) / e.

Y en el caso en que el denominador es una función, aplicaríamos la regla de la derivada de un cociente de funciones.

Espero haberte ayudado.

En bachillerato, solo en casos sencillos: recta, parábola y poco más.