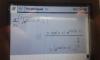
-
me podrian ayudar con el concepto de cambio de base y un ejemplo para entender gracias de algebra lineal

Jordi García
el 7/9/16En caso de que sea el cambio de base de una matriz, te recomiendo ver los siguientes vídeos:
ALGEBRA Matriz de Cambio de Base 01 UNIVERSIDAD unicoos matematicashttps://www.youtube.com/watch?v=wGl-E5LRvac
ALGEBRA Matriz de Cambio de Base 02 UNIVERSIDAD unicoos matematicas
https://www.youtube.com/watch?v=xUfyUGiWH-ESaludos.
-
En un ejercicio de números complejos para pasar de forma binomica a polar este '' 3i '', su angulo me sale 0, es correcto?
Es que al dividir b entre a (3/0) y sacarle arcotangente aun el angulo me sale 0.
¿Me podrían decir si estoy bien?

José Miguel
el 7/9/16Hola Saul, te puedo recomendar que veas el siguiente vídeo:
Numeros complejos 03 - De forma binomica a polarSaludos.
-


Antonio Silvio Palmitano
el 7/9/161) Observa que el argumento de la raíz cuadrada debe ser positivo, y que el denominador debe ser distinto de cero, por lo que podemos factorizar el denominador, y el argumento de la raíz queda:
(x+3) / ( (x+2)(x-2) ), observa que x debe ser distinto de -2, y que x debe ser distinto de 2, luego:
observa que tenemos una expresión fraccionaria completamente factorizada, con tres factores y, como el argumento debe ser positivo, tenemos cuatro posibilidades:
x + 3 >= 0 y x+2>0 y x-2>0, lo que nos conduce al intervalo: (2,+inf)
x+3>=0, y x+2<0 y x-2<0, lo que nos conduce al intervalo [-3,2)
x+3<=0, y x+2>0, y x-2<0, lo que nos conduce al intervalo vacío
x+3<=0, y x+2<0, y x-2>0, lo que nos conduce al intervalo vacío.
Por lo tanto, el dominio de la función es: D = [-3,2)u(2,+inf).
2) Observa que la expresión de la función es un cociente, con la forma: y = u/v, luego planteamos:
u = sen(x^2+1), de donde tenemos (aplicamos regla de la cadena): u ' = cos(x^2+1)*2x
v = (cosx)^3, de donde tenemos (aplicamos regla de la cadena): v ' = 3 * (cosx)^2 * (-senx).
Luego por la regla de derivación de un cociente tenemos que:
y ' = ( u ' * v - u * v ' ) / v^2
y solo queda sustituir las expresiones de u, v u ' y v ' en función de x.
Espero haberte ayudado.
-
Buenasss. a ver si alguien le puede echar un ojo a esta teoria y decirme si esta correcta. GRACIASSS..
Para calcular máximos y mínimos.
Se deriva la función una vez, se iguala a cero y se calcula la solución.
Se vuelve a derivar y se mete las soluciones en la segunda derivada.
Donde la solución sea mayor que 0, tenemos un mínimo y donde sea menor, un máximo.
-


Antonio Silvio Palmitano
el 7/9/16Has expresado bien las raíces como potencias fraccionarias. Luego, debes derivar implícitamente, recordando que y es una función de x, lo haces y queda:
(1/2) * x^(-1/2) + (1/2) *y^(-1/2) * y ' = 0, luego multiplicas en todos los términos por 2, simplificas y queda:
x^(-1/2) + y^(-1/2) * y ' = 0, luego haces pasaje de término y queda:
y^(-1/2) * y ' = - x^(-1/2), luego hacemos pasaje de factor como divisor y queda:
y ' = - x^(-1/2) / y^(-1/2), luego asociamos exponentes a la derecha y queda:
y ' = - (x/y)^(-1/2), luego aplicamos propiedad e las potencias con exponente negativo y queda:
y ´ = - (y/x)^(1/2).
Espero haberte ayudado.
-
Hola amigos, para ver si me ayudan con este ejercicio : hallar un vector de módulo 5u que sea coplanar con A y B y a su vez C con B forma un angulo de 45° grados
-