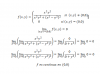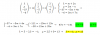-
Una consulta el angulo de 1-√3i seria 5/3 pi?. Ya que el angulo seria igual a arccos a/radio si b>0 y. 2pi-arcos a/radio si b>0,yo uso esa formula,me resulta mas comoda ya que no debo figarme el cuadrante.estaba analizando el ejercicio Z^3=(1-√3i) z conjugado^2
-
- JOSE respecto al ejercicio es Ln elevado a la dos, x,y sub cero
- Determine una aproximación cubica f(x,y)= Ln2(3x-5y+1) alrededor del punto x0 , y0 = (1, -1)
Ayudenme por favor!! Me urge que me den una mano amigos!
2. Estudie la continuidad de la función f(x.y)= x2y2⁄ (x2y2+(x2- y2)2)
(x,y)≠(0,0)
(x,y)=(0,0) en todos los puntos de su dominio.
JOSE RAMOS ayudame por favor, o alguien mas que entienda!! Se los pido


Jose Ramos
el 25/1/20Te recomiendo que veas este video. Ahí podrás ver como se hace una aproximación cúbica. https://www.youtube.com/watch?v=IUO8wiI5_0w. Con respecto al apartado 2, sería así:
-


Jose Ramos
el 25/1/20Al tener la recta de ecuaciones cartesianas x = 0 e y = 0, quiere decir que los puntos de la recta son de la forma (0, 0, z) donde z puede tomar cualquier valor, pues en las ecuaciones no nos limitan el valor de z. De ahí que al tomar puntos cualesquiera de la recta le dan valores a z (los que sean). En tu ejemplo han tomado z = 0 y z=1, pero podrían tomar cualquier otro)
-


Jose Ramos
el 25/1/20En el dibujo se ve claramente que si P está en el plano y r es la perpendicular al plano, la distancia de P a la recta r es la distancia de P a Q, siendo Q el punto de corte de r con el plano.
Te piden justificar que la distancia de P a la recta r es mayor o igual que 3√5/5 y resulta que al calcularla te da precisamente eso, (es igual) con lo que ya has justificado lo que te pide el problema.
-
- Determine una aproximación cubica f(x,y)= Ln2(3x-5y+1) alrededor del punto x0 , y0 = (1, -1)
Ayudenme por favor!! Me urge que me den una mano amigos!
2. Estudie la continuidad de la función f(x.y)= x2y2⁄ (x2y2+(x2- y2)2)
(x,y)≠(0,0)
(x,y)=(0,0) en todos los puntos de su dominio.
JOSE RAMOS ayudame por favor, o alguien mas que entienda!! Se los pido
-
 4ºESO. Inecuación racional.
4ºESO. Inecuación racional.Buenas tardes. Como siempre, gracias de antemano por vuestra ayuda. Adjunto imagen de ejercicio realizado. La pregunta que hago está incluida en la imagen. Es sobre posible tabla alternativa a la creada.


Jose Ramos
el 25/1/20Si haces 1/x-5 ≤ 0 y nos olvidamos de la inecuación de partida, obtenemos como solución: (-∞,5). Fíjate que 1 está en ese intervalo y por tanto sería una solución de la inecuación. Sin embargo 1 no es solución de la inecuación de partida, ya que si evaluamos 1 en dicha inecuación aparece una división por 0.
Por lo tanto. SÍ podemos tomar la solución de la expresión simplificada, extrayendo finalmente de ella aquellos valores que no están definidos para la inecuación de partida, es decir que nuestra solución real sería:
(-∞,5) -{1} = (-∞,1)∪(1,5) que es, a la postre, lo que te da en la tabla.
Espero haberme explicado. Un saludo.
-


Yauset Cabrera
el 25/1/20