-
buenas noches unicos les escribo para solicitar si ustedes pudiesen enviarme ejercicios de ecuaciones que tienen varias expresiones para ser resueltas por el metodo de newton , muchas gracias y buena noche
-


Antonio Silvio Palmitano
el 17/8/16Observa que la integral se resuelve en dos pasos, aplicando el método de las partes:
u = x^2, de donde tenemos: du = 2x*dx
dv = e^(-2x), de donde tenemos: v = -(1/2)e^(-2x)
aplicamos el método y la integral (por el momento indefinida), operamos y queda:
I = -(1/2) * x^2 * e^(-2x) + Integral x * e^(-2x) * dx
observa que la integral secundaria también se puede resolver por partes:
u = x, de donde tenemos: du = dx
dv = e^(-2x) * dx, de donde tnemos: v = -(1/2)e^(-2x)
aplicamos el método, operamos y queda:
I = -(1/2) * x^2 * e^(-2x) -(1/2)x * e^(-2x) + (1/2)*Integral e^(-2x) * dx
observa que la última integral ya es directa (y que la hemos empleado en los planteos que hemos hecho), resolvemos y queda:
I = -(1/2) * x^2 * e^(-2x) -(1/2)x * e^(-2x) - (1/4)*e^(-2x), ahora si definida para evaluar entre 0 y1, lo hacemos y queda:
I = - (1/2)*e^(-2) - (1/2)* e^(-2) - (1/4)*e^(-2) - (0 -0 - 1/4) = - (5/4)*e^(-2) + 1/4 =
= - 5/(4e^2) + 1/4 = ahora tomamos denominador común y queda:
= (-5 + e^2)/(4*e^2) =
= (e^2 - 5)/(4*e^2),
por lo que la igualdad resulta ser verdadera.
Espero haberte ayudado. -


Antonio Silvio Palmitano
el 17/8/16Observa el argumento de la raíz cuadrada:
9 + e^2x = 9 + (e^x)^2
luego, planteamos la sustitución:
u = e^x, de donde teneos: du = e^x * dx, luego: du = udx y finalmente: du/u = dx
el argumento de la raíz cuadrada queda:
9 + u^2
luego, al aplicar la sustitución la integral queda:
I = Integral (1/(uV(9 + u^2)))*du/u = Integral (1/(u^2 * V(9 + u^2)))*du
luego, podemos plantear la sustitución hiperbólica:
u = 3senht, de donde tenemos: du = 3cosht*dt,
el argumento de la raíz cuadrada queda: 9 + u^2 = 9 + (3senht)^2 = 9 + 9(senht)^2 = 9(1 + (senht)^2) = 9(cosht)^2, luego: V(9 + u^2) = 3cosht
luego, aplicamos esta nueva sustitución en la integral, simplificamos y queda:
I = (1/9)*Integral (1/(senht)^2)dt = (-1/9)*cotgh(t) + C. (**)
Luego, a partir de las sustituciones anteriores tenemos:
argsenh(u/3) = t,
u = e^x,
de donde tenemo para reemplazar:
argsenh((e^x)/3) = t.
y solo resta sustituir en la expresión señalada (**).
Espero haberte ayudado. -
Hola unicoos, lamento tener que molestarlos otra vez, pero de verdad necesito su ayuda en las demostraciones. en verdad no se como demostrar lo siguiente. si me pudieran ayudar, en verdad estaria muy agradecido.
P.D: si me podrian recomendar un libro o un link donde pueda encontrar gran parte de las demostraciones de los teoremas de algebra lineal, de verdad se los agradeceria. -
Me podrían ayudar con el punto 52.
Me preguntan:
A. Que tan alto y que tan bajo vuela?
B. Que tan lejos vuela a la izquierda y a la derecha del origen?
Les agradezco.

Antonio Silvio Palmitano
el 17/8/16Observa que x expresa el desplazamiento horizontal, e y expresa el desplazamiento vertical (o altura), por lo tanto, para plantear altura máxima o mínima enemos:
y ' = 0, que corresponde a la ecuación:
2sent = 0, despejamos y queda:
sent = 0
que nos conduce a cuatro valores de t pertenecientes al intervalo:
t1 = 0, sustituimose las expresiones del enunciado y quedan: x = 0, y =0
t2 = pi, sustituimos en dichas expresiones y quedan: x = pi, y = 4
t3 = 2pi, sustituimos en dichas expresiones y quedan: x = 2pi, y = 0
t4 = 3pi, sustituimos en dichas expresiones y quedan: x = 3pi, y = 4
Por lo tanto, tenemos que los puntos:
(0,0) y (2pi,0) son los puntos de altura mínima,
(pi, 4) y (3pi,4) son los puntos de altura máxima.
Espero haberte ayudado. -


Antonio Silvio Palmitano
el 16/8/161)
Observa que tienes una población de 11 elementos, de los cuáles debes seleccionar 5, sin repetir (los invitados son distintos) y sin orden (si invitas a dos, no interesa en qué orden lo haces), por lo tanto tenemos
N = C(11,5) = 11! / (5! * 6!)
2)
Observa que tienes una partición:
a) el matrimonio es invitado (ya ocupaste dos lugares, quedan tres lugares para ocupar por nueve candidatos):
Na = C(9,3) = 9! / (3! * 6!)
b) el matrimonio no es invitado (tienes nueve candidatos para ocupar cinco lugares):
Nb = C(9,5) = 9! / (5! * 4!)
Por la tanto, la cantidad total será:
N = Na + Nb.
3)
Llamemos A y B a las personas enemistadas, y de nuevo tienes una partición:
a) A concurre y B no concurre (te quedan cuatro lugares para ocupar con nueve candidatos):
Na = C(9,4) = 9! / (4!*5!)
b) A no concurre y B si concurre (te quedan cuatro lugares para ocupar con nueve candidatos):
Nb = C(9,4) = 9! / (4!*5!)
c) A no concurre y B no concurre (tienes cinco lugares para ocupar con nueve candidatos):
Nc = C(9,5) = 9! / (5!*4!)
Por lo tanto la cantidad total será
N = Na + Nb + Nc.
Espero haberte ayudado. -
Hola unicoos me gustaría me ayuden con este ejercicio de conjuntos:
Sean los conjuntos K={10,9,8};M={2,3,4}
R1: Es la relación de K en M cuyo enunciado es: "x-y es un número par"
Determine :
a) Condominio o Dominio de imágenes (Di).
b) Conjunto solución(C.S)
c) Dominio de la relación(D)

Antonio Silvio Palmitano
el 17/8/16Observa en la consigna: "x - y es par", entonces tenemos dos opciones:
1) x es par e y es par,
2) x es impar e y es impar,
luego formamos los pares, con primera componente perteneciente al conjunto K, y con segunda componente perteneciente al conjunto M:
la primera opción nos conduce a los pares: (10,2), (10,4), (8,2), (8,4)
la segunda opción nos conduce a un único par: (9,3)
Luego, podemos visualizar:
a) Codominio: el segundo conjunto nombrado al definir la relación, en este caso: M = {2,3,4}
Imágen: conjunto cuyos elementos son las segundas componentes de los pares de la relación, en este caso: {2,3,4] = M
b) Conjunto solución: conjunto cuyos elementos son los pares de la relación: { (10,2), (10,4), (8,2), (8,4), (9,3) }
c) Dominio de la relación: conjunto cuyos elementos son las primeras componentes de los pares de la relación, en este caso: {10, 9, 8} = K.
Espero haberte ayudado.





_Thumb.jpg)


_Thumb.jpg)
_Thumb.jpg)





_Thumb.jpg)

_Thumb.jpg)

_Thumb.png)
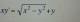

_Thumb.jpg)
