-
-
Hola gente, me pueden ayudar con esta integral impropia?
Me la tomaron en un final y no la pude hacer!.. la llevé a clases de consulta con una profe y cuando la resolvio, le daba que era indeterminada!
pero por las dudas, les consulto a ustedes también
nos daba -∞ + ∞ ... es decir, era una indeterminacion!
pero viendo videos de integrales indeterminadas, cuando calculas la primera "parte" de la indeterminacion y concluis que esa area diverge, automaticamente podes decir que el area total diverge.. es asi??


Antonio Silvio Palmitano
el 18/8/16Observa que x = 1 pertenece al intervalo de integración, y que no pertenece al dominio de la función que debemos integrar. Por lo tanto, debemos plantear una suma de integrales impropias:
I = I1 + I2
cuyos intervalos de integración serán:
D1 = [0 , 1-b)
D2 = (1+b , 2]
Luego, deberemos tomar el límite para b tendiendo a cero por la derecha para resolver.
La primitiva general de la función (puedes emplear la sustitución w = x^2 -1 para hallarla) es:
I = (1/2) * ln|x^2 -1|
Ahora evaluamos para cada subintervalo:
I1 = (1/2) * (ln|(1-b)^2 -1| - ln|-1|) = (1/2) * (ln|-2b + b^2| - 0) = (1/2) * ln|b^2 - 2b| = (1/2) * ln|b(b-2)|
I2 = (1/2) * (ln|3| - ln|(1+b)^2 - 1) = (1/2) * (ln3 - ln|2b + b^2|) = (1/2)*ln3 - (1/2) * ln|b^2 + 2b| = (1/2)*ln3 - (1/2) + ln|b(b+2)|
Luego volvemos a la suma de integrales que hemos planteado:
I = I1 + I2, reemplazamos y queda:
I = (1/2) * ln|b(b-2)| + (1/2)*ln3 - (1/2) + ln|b(b+2)| =(1 /2) * ln3 + (1/2) * (ln|b(b-2)| - ln|b(b+2)|)
luego aplicamos propiedades de los logaritmos, operamos y llegamos a
I = (1 /2) * ln3 + (1/2) * ln|(b-2)/(b+2)|
Por último, tomamos el límite para b tendiendo a cero (por la derecha), teniendo en cuenta que el primer término es constante, y queda:
I = (1 /2) * ln3 + (1/2) * ln|-1| = (1 /2) * ln3 + (1/2) * ln1 = (1 /2) * ln3 + 0 = (1 /2) * ln3, por lo que concluimos que la integral es convergente.
Espero haberte ayudado. -
-
-


Antonio Silvio Palmitano
el 18/8/16Puedes plantear la sustitución (cambio de variable):
u = V(e^x +2), de donde tienes:
u^2 = e^x + 2 (observa que u^2 + 4 = e^x + 6), cuyo diferencial es:
2u*du = e^x * dx.
Sustituyes todo y la integral queda:
I = Integral (u / (u^2 + 4) * 2u*du = 2 * Integral ( u^2 / (u^2 + 4)) * du
luego, planteamos una nueva sustitución: u = 2w, de donde tenemos: du = 2dw, sustituimos y la integral queda:
I = 2 * Integral (4 * w^2 / (4 * w^2 + 4) * 2dw, operamos en la expresión fraccionaria y extraemos factor constante y queda:
I = 4 * Integral (w^2 / (w^2 + 1)) * dw = 4 * Integral (1 - 1 /(w^2 + 1) * dw
a continuación resolvemos la integral término a término y queda:
I = 4 * (w - arctanw) + C.
Queda para que sustituyas w en función de u, y luego u en función de x.
Espero haberte ayudado. -
tengo una duda es sencila pero no enteindo mucho porque
el coseno de 25 π me da -1. no tendria que ser -25?. lo que hice para llaegar a ese - 25 fue, sacar el 25 de adentro del coseno para afuera, calcular el coseno para pi, que es -1 y multiplicarlo.
capaz no funciona pero me quede con la intriga de eso.... -
Alguien me ayuda con el termino de funciones pares e impares. que son, como identificarlas, mas que nada...
gracias de ante mano -


Antonio Silvio Palmitano
el 17/8/16Puedes plantear la sustitución (o cambio de variable): w = 2x,
de donde tienes: dw = 2dx, y luego: dw/2 = dx.
Sustituyes, y la integral queda:
I = Integral e^w * dw/2 = (1/2)*Integral e^w * dw = (1/2)*e^w + C
luego vuelves a la sustitución para recuperar la variable original y llegas a:
I = (1/2)*e^(2x) + C.
Espero haberte ayudado.







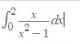







_Thumb.png)





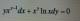

_Thumb.jpg)
_Thumb.jpg)

_Thumb.jpg)
