-
Hola !!
tengo unas consultas a ver si alguien puede ayudarme porfa, en el primer ejercicio me pide calcular el area bajo la funcion y=(raiz(x)) y por arriba la de funcion x-2... lo realize pero creo haberme equivocado , no se donde , ya que el resultado final me da - 6 [u] cosa que no me parece... en el segundo me piden encontrar el volumen de un solido en revolucion ... la verdad no entiendo como hacerlo , alguien con amor al projimo que me ayude?

Antonio Silvio Palmitano
el 17/8/16Observa que las ecuaciones de las curvas se pueden expresar en forma explícita, con x como función de y:
x = y + 2
x = y^2
igualamos para buscar sus puntos de intersección y queda la ecuación:
y^2 = y + 2
luego hacemos pasajes de términos y queda:
y^2 - y - 2 = 0
cuyas soluciones son:
y = -1, que nos conduce a un punto que no pertenece al primer cuadrante:
y = 2, que nos conduce al punto (4,2), que si pertenece al primer cuadrante y es el punto de corte entre las curvas.
Luego, el área puede calcularse, con los límites de integración 0 < y < 2, y observa que a la izquierda de la región se encuentra la parábola, y a su derecha la recta):
Área = Integral ((y + 2) - y^2)*dy = [(1/2) * y^2 + 2y - (1/3) * y^3] para evaluar entre 0 y 2, lo hacemos y queda:
Área = (2 + 4 - 8/3) - 0 = 16/3.
Muchas veces es muy conveniente expresar las curvas con x en función de y, como en este caso.
Espero haberte ayudado. -
Hola! Me podeis ayudar con estos dos ejercicios de limites porfaa ?? Lo que he hecho ha sido dividir cada numero por el coeficiente de mayor grado, tengo las soluciones (+Infinito y -1) pero no me dan. Gracias!!
-


Antonio Silvio Palmitano
el 17/8/16a)
Tenemos que completar binomios elevados al cuadado:
empezamos por ordenar términos y hacer pasaje de términio numérico:
x^2 + 6x + y^2 + 4y = 7
luego agregamos términos según la propiedad uniforme, para completar los binomios al cuadrado desarrollados a la izquierda:
x^2 + 6x + 9 + y^2 + 4y + 4 = 7 + 9 + 4
luego, tenemos los binomios a la izquierda y resolvemos a la derecha:
(x + 3)^2 + (y + 2)^2 = 20
observa que la ecuación corresponde a una circunferencia, cuyos elementos son: centro C(-3,-2) y radio R = V(20);
b)
Observa que el punto P(1,0) pertenece a la circunferencia, ya que sus coordenadas verifican la ecuación.
Luego, derivamos implícitamente (recuerda que y es función de x):
2(x + 3) + 2(y + 2)*y ' = 0
luego evaluamos para el punto de contacto:
2(1 + 3) + 2(0 + 2)*y ' = 0
resolvemos en cada término:
8 + 4y ' = 0
por último, despejamos y obtenemos el valor de la derivada (que será la pendiente de la recta tangente buscada):
y ' = -2.
Por último, como tenemos el punto de contacto y la pendiente, pasamos a la ecuación cartesiana de la recta tangente:
y - 0 = -2(x - 1)
luego cancelamos el término nulo de la izquierda y distribuimos a la derecha y queda:
y = -2x + 2
que es la ecuación cartesiana explícita de la recta tangente pedida.
Espero haberte ayudado. -
Hola estimados amigos de unicoos, solicito de vuestra ayuda para hallar el volúmen del sólido engendrado haciendo girar alrededor de OX la superficie límitada.
La parábola √x+√y=√a ,x=0 ,y=0
Sol. 1/15 πa³
En primer lugar ¿Cómo yo puedo identificar que esa ecuación es una parábola?
Muchisisismas gracias a la persona que me colabore, le doy un abrazo enorme. Saludos.


Antonio Silvio Palmitano
el 17/8/16Recuerda la expresión para calcular un volumen de revolución, alrededor del eje OX:
V = pi * Integral (f(x))^2 * dx.
Comenzamos por despejar y en la ecuación implícita de la curva que nos dan en el enunciado, lo hacemos y queda:
y = (V(a) - V(x))^2
luego elevamos al cuadrado y queda:
y^2 = (V(a) - V(x))^4 = (f(x))^2
Por lo tanto, la integral para el volumen queda expresada:
V = pi * Integral (V(a) - V(x))^4 * dx
Para visualizar los límites de integración, observa la ecuación implícita de la curva, y tenemos que x >= 0, e y >= 0 por ser argumentos de raíces cuadradas, por lo tanto planteamos:
si x = 0, entonces V(y) = V(a), luego y = a;
si y = 0, entonces V(x) = V(a), luego x = a;
y vemos que x toma valores entre 0 y a, por lo que el intervalo de integración queda: 0 <= x <= a.
Volvamos ahora a la integral que tenemos que resolver:
V = pi * Integral (V(a) - V(x))^4 * dx
planteamos la sustitución:
u = V(a) - V(x), de donde tenemos (observa que cuando x = 0 tenemos que u = V(a), y cuando x = a tenemos que u = 0 (**)), luego hacemos pasaje de términos y queda:
V(x) = V(a) - u;
a partir de la expresión de u planteamos su diferencial:
du = (-1/(2V(x)))dx, luego: - 2V(x)du = dx, luego: -2(V(a) - u) *du = dx.
Sustituimos todo en la integral y queda:
V = pi * Integral u^4 * -2(V(a) - u) *du = -2pi * Integral (V(a)*u^4 - u^5) * du
Resolvemos y queda:
V = -2pi * [(V(a) / 5)*u^5 - (1/6)*u^6], que debemos evaluar (recuerda la llamada (**)) entre V(a) y 0, lo hacemos y queda:
V = -2pi * [ 0 - ( (V(a) / 5)*(V(a))^5 + (1/6)*(V(a))^6 )] =
= 2pi * [ a^3 / 5 - a^3 / 6] =
= 2pi * a^3 / 30 =
= pi * a^3 / 15.
Como última apreciación: busca un programa para graficar la curva, que no es una parábola con eje paralelo a OX u OY.
Espero haberte ayudado.
-
Para que valores de xf(x)=6 x 2 -1 es igual a 23, no entendí bien el tema.
-
Hola, quisiera saber cómo se deriva lo siguiente. Realmente estoy muy confundido.
Espero su ayuda. Gracias. -
Holaa Buenas noches ;) es un ejercicio de optimización de funciones, espero y puedan ayudarme: Determinar las dimensiones del mayor triángulo isóceles que se puede inscribir en un circulo de radio 4cm.






_Thumb.jpg)


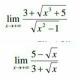

_Thumb.gif)


_Thumb.jpg)


_Thumb.jpg)




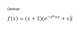

_Thumb.jpg)



_Thumb.jpg)


_Thumb.jpg)
