-
Hola unicoos buenos días , vosotros podrían de favor ayudarme con un límite, no se como hacerlo sin aplicar L'hopital, me piden resolverlo por el método utilizado en la eso . Me lío por el valor absoluto. Gracias de antemano amigos de unicoos.


David
el 10/5/16Cuando x tiende a 1, |x| es x pues la funcion |x|=x tanto a la ziquierda como a la derecha de x=1... (el "punto conflictivo" de |x| es x=0 y no x=1...)
En resumen, que puede olvidarte de ese valor absoluto... Te quedará por tanto limx->1 (x²-1)/(x-1) = 0/0 = limx->1 (x+1)(x-1)/(x-1)=limx->1 (x+1)=2...
Espero te sirva...
P.D. Por identidades notables x²-1=(x+1)(x-19 pues (a+b)(a-b)=a²-b² -
Hola unicoos, me revisarian este ejercicio porfavor?? y queria saber si esa b se puede achicar de alguna forma. Ademas escuche en la clase que les daba c=10, la verdad que nose de donde sacaron eso.. Muchas gracias!
-
ayuda por favor con este ejercicio, suma y multiplica, en base 8 y en base 16, los numeros que en base 2 se escriben 1001011 y 10111001111. graciass
-


Antonius Benedictus
el 10/5/16Ninguna de las afirmaciones a), b) y c) es cierta.
a) La dimensión del espacio final NO ha de ser necesariamente menor o igual que la del iniciaL.
b) No es obligatorio, pues puede darse que f(u_1) = f(u_2)
c) Si x∈gen(u_1,u_2)→f(x)∈gen(f(u_1),f(u_2)) y si resulta que f(u_1) y f(u_2) son colineales (múltiplos de) con f(u_3), entonces f(x) está en gen(u_3). -


David
el 10/5/16Simplemente si la funcion es discontinua en x=2, el denominador será 0 para x=2...
Sustituye x por 2 en el dneominador e iguala a 0...
Para ese valor de "b" obtenido, tendrás que hallar el limite cuando x tiende a 2...
Como en este video.. Asintotas de una función -
hola alguien me podría decir como pasar esta recta reducida a ec parametrica. Creo que la hice bien pero no se. Es una duda muy tonta pero me esta trancando el ejercicio.
Muchas gracias.
Saludos :




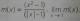






_Thumb.jpg)




_Thumb.jpg)



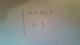


_Thumb.png)




_Thumb.jpg)


