-
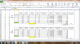
Hola espero poderme expresar de la mejor manera y así se puedan apoyarme con mayor eficacia, en la imagen se muestra que tengo de No. De intervalos (6) y de amplitud (15 o 16) (dependiendo lafórmula), ahora, como con 6 intervalos no me sale correctamente la sumatoria de mi frecuencia porque me faltarían 12, lo que hago es modificarlo a 6.5 (o también puede ser 6.6, o 6.7, según yo) de intervalo, este sube a 7 intervalos y mi amplitud no cambia. Ahí fue como ya resulto correcto la suma de mis frecuencias. Mis dudas son:
1.- ¿siempre debo realizar este proceso?
2.- ¿ el proceso que realice es correcto?, y si no lo es, cómo se realiza debido a que en el video se menciona que la amplitud la podemos cambiar, cosa que yo no hice, sólo cambie mi número de intervalos.
3.- ¿Debo hacer lo contraio, es decir, ir cambiando mi amplitud y respetando mi número de intervalos ? o ¿debo modificar los dos ?
De ante mano le(s) agradezco mucho su atención dada ñ.ñ


David
el 12/4/16Tomes los intervalos que tomes no deberías tener problemas al contarlos a mano. tu problema es que lo estás haciendo con EXCEL y no estáds planteando correctamente las cuentas... Si son 5 intervalos, estos serán [0,20), [20,40), [40,60), [60,80),[80,100]
En el primer intervalo el cero es valido, pero el 0 no...En el 2º intervalo debes contar todos los 20s pero no los 40.. Ahí está el problema de que no te de correctamente la suma....
Por otro lado, no sé cuales son los datos ¡los de la izquierda?....
Si el numero de intervalos es 6, la amplitud de los intervalos será 100/6=16,67....Redondeando al alza 17... Los intervalos serán [0,17), [17,34), [34,51), [51,68),[68,85) ,[85,102)
Y la suma deberá darte igualmente.... Espero te haya ayudado... -
hola me piden analizar continuidad de esa funcion viii) pero no se como resolver el lim x-> -1
aclaro: no puedo usar l'hospital

David
el 12/4/16limx->-1 [2/ln(x+1)]=2/ln0...2/(-∞)=0....
Te sugiero este video... Estudio completo de una funcion logaritmica -
Cordial saludo:
Me han puesto a resolver el siguiente ejercicio (IMAGEN ANEXA), el cual me ha parecido algo engañoso ya que esta muy sencillo y lo he resuelto de la siguiente manera:
a) Iguale ambas expresiones, es decir: F=(π*Po*Ro∧4)/(8*n*l)=(π*P*R∧4)/(8*n*l), como π/(8*n*l) son valores constantes para ambas expresione entonces se "eliminan", quedando: Po*Ro∧4/P*R∧4, donde al despejar resulta: (Ro/R)∧4=(P/Po).
b) De la formula F=(π*P*R∧4)/(8*n*l) despeje P quedando P=(F*8*n*l)/(π*R∧4) y al reducir al radio (R) a 3/4, entonces P=(F*8*n*l)/(π*(¾R)∧4) y operando P=256/81* (F*8*n*l)/(π*R∧4) y como P=(F*8*n*l)/(π*R∧4), entoneces resulta ≈ 3.1P
Pido el favor me comenten si esta bien realizado. Graciasb) De la formula F=(π*P*R∧4)/(8*n*l) despeje P quedando P=(F*8*n*l)/(π*R∧4) y al reducir al radio (R) a 3/4, entonces P=(F*8*n*l)/(π*(¾R)∧4) y operando P=256/81* (F*8*n*l)/(π*R∧4) y como P=(F*8*n*l)/(π*R∧4), entoneces resulta ≈ 3.1P
Pido el favor me comenten si esta bien realizado. Gracias">
-
Hola, necesitaría ayuda con este problema de logaritmo complejo:
"De entre todas las raíces enésimas del número complejo:
1 + √3
¿Hay alguna raíz cuyo logaritmo principal sea real?"
Desde ya, Muchas gracias.

David
el 12/4/16En forma polar es 2,60º....
Las raices enesimas tendrán de argumento (o fase) (60+360.n)/n... Será real si para algun valor entero de n, el argumento te da 180, 360º, 540º, 720º... en general 180.k, siendo k un numero entero...
Por ejemplo... (60+360.n)/n = 180.... 60+360.n = 180.n... 60=-180.n...n=-1/3, que no puede ser, por darte negativo y racional...
(60+360.n)/n = 360.... 60+360.n = 360.n... que no tiene solucion...
(60+360.n)/n = 540... 60+360.n = 540.n...60=180.n... n=1/3, que no es entero...
(60+360.n)/n = 720... 60+360.n = 720.n...60=360.n... n=1/6, que no es entero...
No hay ninguna raiz enesima que sea real... -


David
el 12/4/16Por igualación... 4-y²=4-4y.... y²-4y=0... y(y-4)=0... de donde y=0 e y=4... Para y=0, x=4... Para y=4, x=-12...
Por tanto deberás hacer la integral entre -12 y 4 de la resta de ambas funciones... Te sugiero estos vídeos... Area entre funciones 01 -
Hoola! He intentado hacer esta integral, primero la separé y en la segunda fracción me dí cuenta de que había una derivada, pero no acabo de llegar al resultado correcto. Gracias!
-


David
el 12/4/16¿Y tu duda es?... Te toca hallar el dominio... Dominio funcion irracional
Tambien te tocará derivar... Regla de la cadena
Y representarlas...
Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. #nosvemosenclase Nos cuentas ¿ok? -
Hoola! ¿Dónde aprecian el error en esta integral que intenté hacer por cambio de variable? Seguro que está mal, pero no veo el error. Por si no se ve muy bien, el enunciado es ∫√x . (4x²+5x-6) dx.
PD: si es posible, resolverla utilizando cambio de variable. Gracias!

JBalvin
el 12/4/16Cuando vayas a resolver una integral, te. Pueden dar diferentes resultados ya que una función tiene infinitas primitivas.
A mi me ha pasado que tengo que resolver la integral de x/√(1+x^2) y llego a una primitiva con funciones trigonométricas, pero si te das cuenta (1/2)√(1+x^2) es otra primitiva, y cuando lo fui a comprobar me salia esta. La forma segura para comprobar si la integral esta bien es derivando



_Thumb.png)
_Thumb.jpg)







_Thumb.jpg)

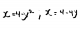
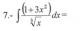
_Thumb.jpg)




