-
Hola
Cómo se demuestra estas identidades trigonométricas??
a) cos ( π/2 - a ) = sen a
b) 2cos(a) - sen(2a)= 2cos² (a) / 1+ sen (a)
c) (cosec(a) - cot (a))² = 1- cos(a) / 1 + cos (a)

Miquel Martos Doroteo
el 13/4/16Buenas noches. Te dejo aquí la primera identidad. Es muy importante que repases el valor del seno, del coseno y de la tangente de los ángulos fundamentales, que son 0, 30, 45, 60 y 90º.
También es importante que sepas la fórmula del coseno de la suma/resta de ángulos:
cos(a-b)=(cos(a)*cos(b))+(sen(a)*sen(b))
cos(a+b)=(cos(a)*cos(b))-(sen(a)*sen(b)) -
calcula el termino general de una progresión aritmética
A6= -7 y A12= -12 -
suma de los términos de una progresión aritmética
A los trece primeros números que acaban en trece
B los números del 1 al 100
COMO HARIA ESTOS DOS ??

David
el 13/4/16Los numeros del 1 al 100 son una progresion aritemtica con a1=1 y d=1.. El termino general será an=1+(n-1).1=1+n-1=n
Recuerda que Sn=(a1+an).n/2.. Por tanto (1+100).100/2...
Para el a), debes hallar S13....La progresion será 13,113,213,313.... El primer termino será 13 y la diferencia es 100
El termino general será an=13+(n-1).100=13+100n-100=100n-87
Por tanto a13=100.13-87=1300-87=1213
Y S13=(13+1213).13/2
Te sugiero los vídoes de progresiones aritmeticas... Se trata de ser ordenado y tener un poco de sentido comun... Progresiones aritméticas
Tengo la sospecha de que no has visto ningun vídeo de esa lección. De lo contrario, al menos el b), no debería haberte supuesto un problema. SALU2! -
holaa!el tema trata de la suma de los términos de una progresión aritmética y el enunciado es: calcula la suma de A los veinte primeros múltiplos de 3 como lo haría?
-
-
Tengo una duda con la matriz escalar. Se que los elmentos de la diagonal principal deben ser los mismos, pero es necesario que todos los otros sean ceros? porque todos los ejemplos que encuentro son con todos 0 fuera de la diagonal. Saludos!
-


David
el 13/4/16Ese ejercicio es muy muy complicado. De nivel universitario y digno de una olimpiada matematica.
Voy a intentar ayudarte un poco... Debes construir un MEGAARBOL de diferentes posibilidades...
(1) En la primera planta se baja un sola persona, tienes 6 opciones.. Quedan 5 personas y 3 plantas por subir. En ese caso, en la 2ª planta puede ocurrir:
(1.1) Que se baje una sola persona (5 opciones).. Quedarán 4 personas y 2 plantas por subir.
En ese caso en la 3ª planta, diferentes opciones.... (1.1.1) Que se baje solo una (4 opciones). Quedarán 3 personas y 1 planta por subir.
....................................................................................................(1.1.2) Que se bajen 2 personas. C4,2 = 4! /2! 2! =6 opciones. Quedarán 2 personas y 1 planta por subir
....................................................................................................(1.1.3) Que se bajen 3 personas. C4,3 = 4! /3! 2! =2 opciones. Quedará 1 persona y 1 planta por subir
....................................................................................................(1.1.4) Que se bajen 4 es imposible pues en cada planta debe bajarse al menos una y ya no quedaría ninguna para bajarse en la ultima planta...
Las diferentes opciones 6.5.12=360
(1.2) Que se bajen dos personas C5,2=5! / 2! 3! = 5.4.3.2 / (2.3.2)=10 opciones.... Quedarían 3 personas, 2 plantas por subir
En ese caso en la 3ª planta, diferentes opciones ...(1.2.1) Que se baje solo una (3 opciones). Quedarían 2 personas, 1 planta por subir
...................................................................................................(1.2.2) Que se bajen 2 personas. C3,2 = 3! /2! 1! =3 opciones. Quedaría 1 persona, 1 planta por subir...
...................................................................................................(1.1.3) Que se bajen 3 es imposible pues en cada planta debe bajarse al menos una y ya no quedaría ninguna para bajarse en
la ultima planta
Las diferentes opciones 6.10.6=360
(1.3) Que se bajen 3 personas C3,2=5! / 2! 3! = 5.4.3.2 / (2.3.2)=10 opciones.... Quedarían 2 personas, 2 plantas por subir
En ese caso en la 3ª planta se bajar una persona (2 opciones) y en la 4ª la que queda (1 opcion)
Las diferentes opciones 6.10.2=120
La solucion, si no me he confundido 360+360+120=840 posibilidades...
Y todo ello teniendo en cuenta que solo se ha bajado una en la primera planta. Deberás repetir el proceso pensando en que se han parado 2 o 3 personas en la primera planta -
Hola, no sé como hacer este ejercicio, sé que es una elipse pero, no me da el resultado.
Halla la ecuación del lugar geométrico cuya suma de distancias a los puntos A(0,1) y B(0,-1) es siempre 8.



_Thumb.png)



_Thumb.jpg)

_Thumb.jpg)

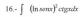






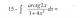






_Thumb.png)
