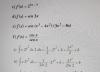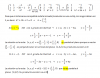-
Hola, tengo que encontrar el valor de z utilizando la tabla de la normal, pero no sé como hacer este ejemplo: P (k<=Z) = 0,10 . Sé que debería hacer la búsqueda al revés, pero la probabilidad 0,10 no aparece en la tabla, así que no sé qué hacer. Gracias por vuestra ayuda.


Jose Ramos
el 21/1/20Cuando en ese caso el valor de probabilidad es menor que 0,5 (La tabla toma valores de probabilidad de 0,5 en adelante) quiere decir que z es negativo. Tienes que buscar el valor de z que hace P(k<=z) = 1-0,10 = 0,9 que en este caso sería: 1,28. Entonces el valor de z que buscas inicialmente es z = -1,28.
Expresado de otro modo sería: P (k <=z) = 0, 10 entonces P (k <= -z) = 0,9, -z = 1,28, entonces z = -1,28.
-


Antonio Silvio Palmitano
el 21/1/20Planteas las expresiones de los vectores:
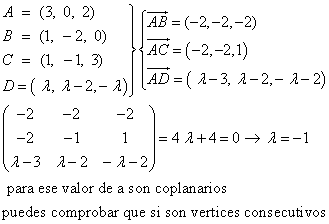
u = AB = < -2 ; -2 ; -2 >,
v = AC = < -2 ; -1 ; 1 >;
luego, planteas la expresión del producto vectorial entre estos dos vectores, y queda:
u x v = < -4 ; 6 ; -2 > = n;
luego, con las coordenadas del punto A(3,02), y con las componentes del vector n, planteas la ecuación cartesiana implícita del plano determinado por los puntos A, B y C, y queda:
-4*(x - 3) + 6*(y - 0) -2*(z - 2) = 0, distribuyes en los tres términos del primer miembro, cancelas el término nulo, reduces términos semejantes, y queda:
-4*x + 6*y - 2*z + 16 = 0, restas 16 en ambos miembros, luego divides por -2 en todos los términos, y queda:
2*x - 3*y + z = 8 (1).
Luego, tienes planteada la expresión del cuarto punto: D(λ,λ-2,-λ);
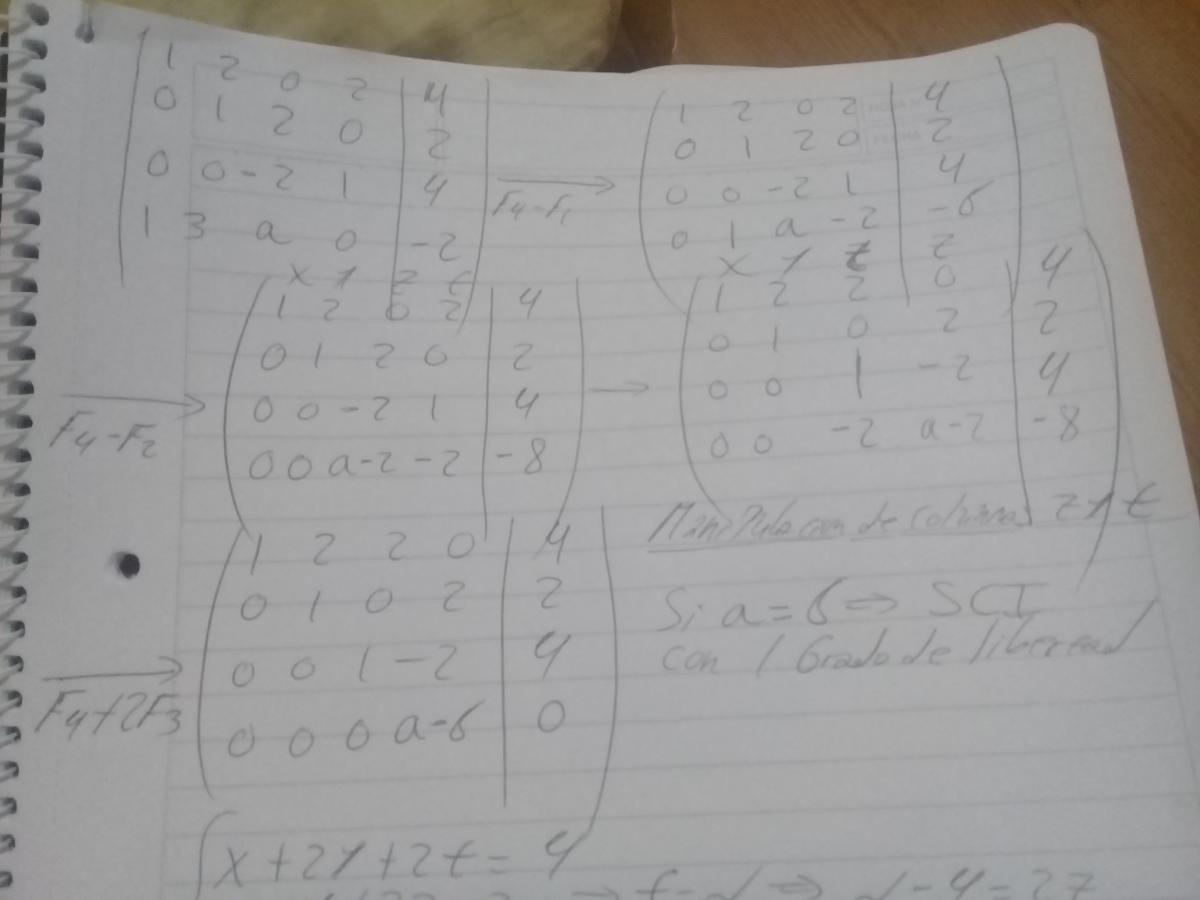
luego, como tienes en tu enunciado que este cuarto punto debe pertenecer al plano determinado por los puntos A, B y C, reemplazas sus coordenadas en la ecuación del plano señalada (1), y queda:
2*λ - 3*(λ - 2) + (-λ) = 8, desarrollas los dos últimos términos y reduces términos semejantes en el primer miembro, y queda:
-2*λ + 6 = 8, restas 6 en ambos miembros, luego divides por -2 en ambos miembros, y queda:
λ = -1;
luego, reemplazas el valor del parámetro que tienes remarcado en la expresión del punto D, resuelves coordenadas, y queda:
D(-1,-3,1).
Luego, si consideras que los vértices consecutivos están en el orden ABDC (haz un dibujo para visualizar mejor la situación), entonces tienes que los dos pares de vectores:1°)
AB y CD,
2°)
AC y BD,
deben estar conformados por vectores coincidentes;
luego, planteas las expresiones de los vectores consignados en ambos grupos, y queda:
1°)
AB = < -2 ; -2 ; -2 >,
CD = < -2 ; -2 ; -2 >,
que son vectores coincidentes,
2°)
AC = < -2 ; -1 ; 1 >,
BD = < -2 ; -1 ; 1>,
que son vectores coincidentes;
y, como tienes que además los cuatro vectores son coplanares, entonces puedes concluir que los puntos A, B, C y D son los vértices de un paralelogramo.
Espero haberte ayudado.
-
Hola , saludos!!!
Bueno quiero saber si: Dadas dos rectas S yM paralelas entre si cortadas por L y R (rectas), se cumple que L y R son paralelas entre si si la distancia de las intersecciones entre SL y Ml son iguales a las distancia SR Y MR.