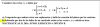-
Cómo puedo formular este enunciado en un sistema de ecuaciones de variables x e y?
El perímetro de un triángulo isósceles mide 65m, y cada uno de los lados iguales mide el doble del lado desigual. ¿Cuánto mide cada lado?
-


Antonio Silvio Palmitano
el 22/1/20Vamos con un desarrollo por etapas, que espero te sea útil.
1°)
Tienes el punto: A(1,3,-2),
y tienes la ecuación vectorial paramétrica de la recta L: <x,y,z> = λ*<1,0,1> + <1,2,0>, con λ ∈ R, cuyo vector director es: u = <1,0,1>;
y tienes que calcular las coordenadas del punto P(x,y,z) que es el punto simétrico al punto A con respecto a la recta L;
luego, con las coordenadas del punto A, y con las componentes del vector u, planteas la ecuación cartesiana implícita del plano Σ que perpendicular a la recta L y que pasa por el punto A, y queda:
1*(x - 1) + 0*(y - 3) + 1*(z + 2) = 0, cancelas el término nulo, distribuyes, y queda:
x + z + 1 = 0 (1);
luego, planteas la intersección de la recta L con el plano Σ, a fin de determinar su punto de intersección (M), para ello, planteas las ecuaciones cartesianas paramétricas de la recta L a partir de su ecuación vectorial paramétrica que tienes en tu enunciado, y queda:
x = λ + 1 (2),
y = 2 (3),
z = λ (4);
luego, sustituyes las expresiones señaladas (2) (4) en la ecuación señalada (1), y queda:
λ + 1 + λ + 1 = 0, reduces términos semejantes, y queda:
2*λ + 2 = 0, y de aquí despejas: λ = -1;
luego, reemplazas este valor en las ecuaciones señaladas (2) (3) (4) (en realidad, en la primera y en la última de ellas), resuelves, y queda:
x = 0,
y = 2,
z = -1,
que son las coordenadas del punto de intersección de la recta L con el plano Σ, cuyas expresión es: M(0,2,-1);
luego, como tienes en tu enunciado que el punto A y el punto P son simétricos con respecto a la recta L, entonces tienes que M es el punto medio del segmento determinado por los puntos A y P, y por ello tienes también que los vectores: AM y MP son equivalentes, por lo que puedes plantear la ecuación vectorial:
MP = AM, planteas las expresiones de los vectores, y queda:
< x-0 , y-2 , z+1 > = < 0-1 , 2-3 , -1+2 >,
cancelas el término nulo en las primeras componentes, resuelves las expresiones de las componentes en el segundo miembro, y queda:
< x , y-2 , z+1 > = < -1 , -1 , 1 >, y por igualdad entre expresiones vectoriales igualas componente a componente, y quedan las ecuaciones:
x = -1,
y - 2 = -1, de aquí despejas: y = 1,
z + 1 = 1, de aquí despejas: z = 0,
por lo que tienes que la expresión del punto simétrico al punto A con respecto a la recta L es: P(-1,1,0).
2°)
Tienes el punto: B(-2,0,2),
y tienes la ecuación cartesiana implícita del plano ∏: x + y - z = 2, donde tienes que su vector normal es: n = <1,1,-1>,
y tienes que calcular las coordenadas del punto Q(x,y,z), que es la proyección del punto B sobre el plano Π;
luego, con las coordenadas del punto B y con las componentes del vector n, planteas las ecuaciones cartesianas paramétricas de la recta R que es perpendicular al plano Π, y queda:
x = μ - 2 (5),
y = μ (6),
z = -μ + 2 (7),
con μ ∈ r;
luego, sustituyes las expresiones señaladas (5) (6) (7) en la ecuación del plano Π, y queda:
μ - 2 + μ - (-μ + 2) = 2, distribuyes el tercer término y reduces términos semejantes en el primer miembro, y queda:
3*μ - 4 = 2, y de aquí despejas: μ = 2;
luego, remplazas este valor en las ecuaciones señaladas (5) (6) (7), resuelves, y queda:
x = 0,
y = 2,
z = 0,
por lo que tienes que la expresión del punto que es proyección del punto B sobre el plano Π es: Q(0,2,0).
3°)
Planteas la expresión de un vector director de la recta K que pasa por los puntos P y Q, y queda:
v = PQ = < 0+1 , 2-1 , 0-0 > = < 1 , 1 , 0 >;
luego, con las coordenadas de uno de los puntos de la recta (nosotros elegimos el punto Q), y con las componentes del vector v, planteas las ecuaciones cartesianas paramétricas de la recta K, y queda:
x = φ,
y = φ + 2,
z = 0,
con φ ∈ R.
Espero haberte ayudado.
-
Buenas, no consigo resolver el siguiente problema:
Observando el vuelo que describe una abeja desde loa alto de un árbol hasta el suelo, comprobamos que la altura a la que se encuentra desde que sale del árbol hasta que aterriza, se puede calcular por medio de esta función: A(t) = -1t2+6t+16 donde "t" es el tiempo en segundos y A(t) nos da la altura en metros en función del tiempo.
1 calcula la altura a la que se encuentra
2 calcula cuánto tiempo tarda en llegar al suelo
gracias.


Antonio Silvio Palmitano
el 22/1/201)
Evalúas la expresión de la función para el instante inicial: t = 0, y queda:
A(0) = -1*02 + 6*0 + 16, resuelves el segundo miembro, y queda:
A(0) = 16,
por lo que tienes que la altura inicial es 16 m.
2)
Planteas la condición de llegada al suelo (la altura es igual a cero), y queda la ecuación:
A(t) = 0, sustituyes la expresión de la función en el primer miembro, y queda:
-1*t2 + 6*t + 16 = 0, multiplicas por -1 en todos los términos, y queda:
1*t2 - 6*t - 16 = 0,
que es una ecuación polinómica cuadrática (te dejo la tarea de resolverla), cuyas soluciones son:
a)
t = -2 s, que no tiene sentido para este problema,
b)
t = 8 s, que es el valor del instante en el cuál la abeja llega al nivel del suelo.
Espero haberte ayudado.
-
¿Qué significa cuando algo es constante y proporcional?
Por ejemplo, en el libro de Aritmética de Baldor dice:
Peso:No es posible determinar directamente la cantidad de materia que contiene un cuerpo; pero se sabe que mientras mayor es su masa material, mayor es la atracción que la gravedad ejerce sobre él, es decir, mayor es su peso. Esta relación entre la masa material y el peso es constante y proporcional.
Observando los cuerpos que se presentan en la Naturaleza y separando mentalmente todas sus otras cualidades, para fijarnos sólo en la atracción que la gravedad ejerce sobre ellos, llegamos al concepto de peso.
Debido a la relación constante que hay entre la masa material de un cuerpo y su peso, hasta el punto de expresarse con el mismo número (551), prescindiremos en esta obra de hablar de un modo sistemático acerca de la masa material de los cuerpos, para referirnos sólo a su peso. Pero téngase presente que los conceptos de masa material y peso son distintos.
No pido que me hagan el trabajo pero esto me parece algo confuso.
Espero su respuesta, gracias :)


Antonio Silvio Palmitano
el 22/1/20La magnitud Peso (P) y la magnitud Masa Material (M) son proporcionales porque se relacionan por medio de una ecuación de la forma:
P = k*M,
donde k es una constante.
Si recuerdas tus clases de Física, entonces tienes que P es la expresión del módulo del peso de un cuerpo, que M es la expresión de su masa material, y que la constante de proporcionalidad es el módulo de la aceleración gravitatoria terrestre, que se designa generalmente "g", por lo que la ecuación queda:
P = g*M, conmutas factores en el segundo miembro, y queda:
P = M*g.
Espero haberte ayudado.
-
 Para Jose Ramos.
Para Jose Ramos.4º eso. Sistema de inecuaciones con dos incógnitas.
Hola Jose, este es el problema que te comentaba en otro post de hace un rato. ¿Serías tan amable de generar el sistema? A ver si en este caso veo mejor su lógica y termino de entender el problema anteriormente planteado. En este nuevo problema (actividad 24) he creado el sistema e inecuaciones que ves, pero me da dos semiplanos con una intersección absurda.

José Antonio
el 22/1/20Hola,
pruebe a completar la tabla, añadiendo una última fila con las restricciones:
Número Tomates Pasta Lote A X 2 1 Lote B Y 3 2 350 200 Si lee en vertical las líneas, podrá ver que 2x+3y menor o igual que 350 y x+2y menor o igual que 200.
Fijándonos en los tomates puede ver que cada lote A gasta 2 y cada lote B gasta 3, y en total no puede gastar más de 350 tomates, que son los que tienen en la tienda.
Análogo para la pasta.
Espero que esto le sirva.


JOSE ANTONIO
el 22/1/20 Muchas gracias Jose Antonio por tu ayuda . Es posible que ya lo tenga. Te adjunto gráfico Geogebra con el sistema de desigualdades que he construido, añadiendo un filtro para x e y al objeto de reflejar únicamente números naturales. Si finalmente el problema está bien hecho lo idóneo sería conseguir, de manera automática con GG la lista de puntos (x,y) que verifiquen la pregunta del problema (cuantos lotes de cada tipo se pueden completar).
Muchas gracias Jose Antonio por tu ayuda . Es posible que ya lo tenga. Te adjunto gráfico Geogebra con el sistema de desigualdades que he construido, añadiendo un filtro para x e y al objeto de reflejar únicamente números naturales. Si finalmente el problema está bien hecho lo idóneo sería conseguir, de manera automática con GG la lista de puntos (x,y) que verifiquen la pregunta del problema (cuantos lotes de cada tipo se pueden completar).