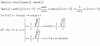-
Se justifica porque los complejos son pares ordenados de números reales, entonces, como sus componentes son números reales, y por las definiciones de suma y producto de complejos, cumplen estas mismas propiedades. ¿Es correcto?
-
hola soy nuevo y no se como va esto donde me resuelven mis dudas
-
¿Que son los Síndromes ? (Matemática Abstracta o Discreta)
Mi duda es: Qué es el Síndrome y sobre todo como se asocia a el líder de clase corres poniente.
Ej. Porqué el Síndrome "111" esta asociado a "01100" o porqué el "110" al "10000".
Nota: lo demás si lo entiendo, solo no comprendo como se vincula el Síndrome al Líder de Clase.


Antonius Benedictus
el 14/1/20¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).