-
-
 Repito mi consulta de ayer. Un saludo:
Repito mi consulta de ayer. Un saludo:4ESO- resolver 2 inecuaciones dadas a partir de una gráfica.
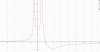
El ejercicio dice literalmente: “utilizar la gráfica del polinomio P(x) = x³ + 6x² - x +30 para resolver las inecuaciones a) x³ + 6x² - x +30 > 0 y b) x³ + 6x² - x +30 ≤ 50”.
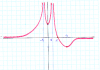
El primer paso dado (como venía haciendo hasta ahora) ha sido intentar averiguar, por Ruffini, las posibles raíces que igualaran a cero la ecuación que indicada. No he conseguido nada, ni siquiera la única raíz (≈ -6,8) que sé que existe porque me la ha dado Geogebra (GG). Las dos inecuaciones tienen solución gráfica e intervalos, como veréis en la imagen adjunta, pero no sé como conseguir las soluciones que me da GG. Os agradezco la ayuda. Buenas noches.
4ESO- resolver 2 inecuaciones dadas a partir de una gráfica.


Jose Ramos
el 13/1/20La gráfica está clara. Fíjate que la solución de la inecuación > 0 son los puntos del eje X para los que la función está por encima de dicho eje (la función es positiva). Eso ocurre para x > -6,8.
Para la inecuación <= 50, trazas una linea paralela al eje X que corte al eje Y en 50 y la solución son los valores del eje x que hacen que la función esté por debajo de dicha línea.


JOSE ANTONIO
el 13/1/20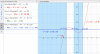 Jose Ramos muchas gracias por tu contestación, la cual me ha sido de una gran ayuda.
Jose Ramos muchas gracias por tu contestación, la cual me ha sido de una gran ayuda.Como me has dicho he añadido en +50 una recta paralela al eje X y ahora lo veo, aunque lo mío me ha costado (adjunto nueva imagen con solo la desigualdad ≤ 50 para mayor claridad). No obstante sigo sin saber cómo consigo calcular los valores de x en las dos desigualdades (-6,8 para >0 y -5,53/-2,15/1,68 para ≤ 50. Lo he intentado por todos los medios pero no doy con la tecla. Me podrías por favor orientar. Gracias de nuevo.


Jose Ramos
el 13/1/20Averiguar los valores que determinan los extremos de los intervalos donde se encuentra la solución, equivale a resolver la ecuación x3+6x2-x+30=50, es decir x3+6x2-x-20=0. Esto se puede intentar por Ruffini, pero en este caso no nos va a salir ya que las soluciones no son enteras. La resolución de este tipo de ecuaciones se sale del ámbito del bachillerato y se resuelven gráficamente con GG o por métodos numéricos que se estudian en la Universidad. Así que no te preocupes si no te sale.
-


Breaking Vlad
el 15/1/20Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado, pero no olvidéis de adjuntarlo de forma LITERAL, para saber que os piden. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)