-
Hola Alguien me puede ayudar con este ejercicio por favor. Muchas gracias
-

 Hola, me gustaría saber como se sabe que se cruzan para resolverlo de esa forma, porque el enunciado no nos dice nada de que se crucen o que son paralelas. Gracias!!!
Hola, me gustaría saber como se sabe que se cruzan para resolverlo de esa forma, porque el enunciado no nos dice nada de que se crucen o que son paralelas. Gracias!!! -
Hola!
Tengo una duda práctica a la hora de construir un volumen para una pieza de escalada y calcular los ángulos de corte.
Básicamente quiero hacer una pequeña pirámide de 3 lados iguales y sin suelo.
Calcular las distancias y ángulos de cada pieza en 2d para saber su dimensión una vez montada en 3d resulta fácil. Y también resulta fácil hacer este montaje en 3d con un elemento casi plano como por ejemplo una cartulina. Pero la cosa se complica cuando quiero construir esta pirámide en madera de 19mm de grosor.Aquí podéis ver una primera imagen de la pirámide vista desde arriba.
Una segunda imagen del despiece de cada parte.
Y una tercera imagen donde se plantea mi problema, que es saber el anglo de corte de cada pieza, para que al unirse encajen perfectamente.
En realidad la información que me faltaría es la de dos ángulos:
1. El ángulo que forma la unión de dos piezas por sus vértices. Son 3 uniones pero sería un mismo ángulo.
2. El ángulo que forman las piezas con el suelo.
Estos ángulos son importantes, ya que es el ángulo al que debo de poner la sierra para cortar las maderas.
Claro, podría hacerlo a ojo y poco a por ir ajustando, pero como quiero hacer distintas pirámides con diferentes alturas, lo ideal sería poder sacar una formula.
A alguien se le ocurre la solución?
Gracias!

David
el 29/1/20Hola! Me encantaría ayudarte, pero no respondemos dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Hola muy buenas , queria pedir ayuda para resolver el siguiente ejercicio, porfavor ya que no me sale la asintota horizontal ni oblicua. Agradeceria que me lo resolvierais y no me pasarais un link de un video, que ya los he visto todos :c
"Determina el dominio y las asintotas de la función f(x)= raiz(x^3/x-1)"
gracias de antemano :)


Antonio Silvio Palmitano
el 5/1/20Vamos con una orientación.
Tienes la expresión de la función: f(x) = √(x3/[x-1]), extraes factores, y queda: f(x) = |x|*√(x/[x-1]) = |x|*√(1 + 1/[x-1]),
cuyo dominio es: D = (-∞;0] ∪ (1;+∞) (te dejo la tarea de hacer los planteos necesarios para determinar el dominio de la función, para lo que debes plantear que el argumento de la raíz cuadrada debe ser mayor o igual que cero).
1°)
Estudiamos la posible existencia de asíntotas horizontales:
a)
Lím(x→-∞) f(x) = Lím(x→-∞) |x|*√(1 + 1/[x-1]) = Lím(x→-∞) -x*√(1 + 1/[x-1]) = +∞,
por lo que la gráfica de la función no presenta asíntota horizontal izquierda;
b)
Lím(x→+∞) f(x) = Lím(x→+∞) |x|*√(1 + 1/[x-1]) = Lím(x→+∞) x*√(1 + 1/[x-1]) = +∞,
por lo que la gráfica de la función no presenta asíntota horizontal derecha.
2°)
Estudiamos la posible existencia de asíntotas verticales:
a)
La gráfica no presenta asíntota vertical en x = 0, ya que la función está definida en este valor: f(0) = 0,y su límite para este valor queda:
Lím(x→0-) f(x) = Lím(x→0-) |x|*√(1 + 1/[x-1]) = Lím(x→0-) -x*√(1 + 1/[x-1]) = 0;
b)
Lím(x→1+) f(x) = Lím(x→1+) |x|*√(1 + 1/[x-1]) = Lím(x→1+) x*√(1 + 1/[x-1]) = +∞,
por lo que la gráfica de la función sí presenta asíntota vertical cuya ecuación es: x = 1.
3°)
Estudiamos la posible existencia de asíntotas oblicuas.
a)
Lím(x→-∞) f(x)/x = Lím(x→-∞) |x|*√(1 + 1/[x-1])/x = Lím(x→-∞) -x*√(1 + 1/[x-1])/x = Lím(x→-∞) -√(1 + 1/[x-1]) = -1 = mi,
Lím(x→-∞) (f(x) - mi*x) = Lím(x→-∞) (|x|*√(1 + 1/[x-1]) - (-1)*x) = Lím(x→-∞) (-x*√(1 + 1/[x-1]) + x) = Lím(x→-∞) -x*(√(1 + 1/[x-1]) -1) = -1/2 = bi,
por lo que tienes que la gráfica de la función presenta asíntota oblicua izquierda, cuya ecuación cartesiana explícita es: y = -x - 1/2;
b)
Lím(x→+∞) f(x)/x = Lím(x→+∞) |x|*√(1 + 1/[x-1])/x = Lím(x→+∞) x*√(1 + 1/[x-1])/x = Lím(x→+∞) √(1 + 1/[x-1]) = 1 = md,
Lím(x→+∞) (f(x) - md*x) = Lím(x→+∞) (|x|*√(1 + 1/[x-1]) - 1*x) = Lím(x→+∞) (x*√(1 + 1/[x-1]) - x) = Lím(x→+∞) x*(√(1 + 1/[x-1]) -1) = 1/2 = bd,
por lo que tienes que la gráfica de la función presenta asíntota oblicua derecha, cuya ecuación cartesiana explícita es: y = x + 1/2.
Haz el intento de desarrollar el planteo para determinar el dominio de la función, y para resolver todos los límites que hemos expuesto, y si te resulta necesario no dudes en volver a consultar.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 4/1/20Tienes la ecuación: x3*z2 - x*y*z3 = 2, que corresponde a una superficie de nivel de la función:
F(x,y,z) = x3*z2 - x*y*z3, que es una función continua y también diferenciable en R3,
cuyas derivadas parciales quedan expresadas:
Fx = 3*x2*z2 - y*z3,
Fy = -x*z3.
Fz = 2*x3*z - 3*x*y*z2;
y tienes que la ecuación de tu enunciado define implícita mente a z como función de x e y: z = f(x,y),
en un entorno del punto: A(1,1,-1),
y observa que la función toma el valor: zA = f(1,1) = -1,
y que las derivadas parciales de la función F toman los valores:
Fx(1,1,-1) = 4,
Fy(1,1,-1) = 1,
Fz(1,1,-1) = -5.
Luego, derivas implícitamente con respecto a x en ambos miembros de la ecuación de tu enunciado (observa que debes aplicar la Regla de la Cadena, debido a que z es una función f que depende de x e y), y queda:
Fx + Fz*fx = 0, de donde despejas: fx = -Fx/Fz (1),
Fy + Fz*fy = 0, de donde despejas: fy = -Fy/Fz (2);
luego, evalúas las expresiones de las derivadas parciales de la función f señaladas (1) (2) para x = 1 e y = 1, para ello reemplazas los valores de las derivadas parciales de la función F que ya tienes evaluadas, y queda:
fx(1,1) = -4/(-5) = 4/5,
fy(1,1) = -1/(-5) = 1/5.
Luego, planteas la ecuación general del planto tangente a la gráfica de una función de dos variables (f), cuyo punto de contacto es A, y queda:
z = zA + fx(xA,yA)*(x - xA) + fy(xA,yA)*(y - yA), reemplazas los valores de las coordenadas del punto A(1,1,-1), y queda:
z = -1 + fx(1,1)*(x - 1) + fy(1,1)*(y - 1), reemplazas los valores de las derivadas parciales de la función f evaluadas para el punto A, y queda:
z = -1 + (4/5)*(x - 1) + (1/5)*(y - 1), distribuyes, reduces términos semejantes, ordenas términos, y queda:
z = (4/5)*x + (1/5)*y -2, multiplicas por 5 en todos los términos, y queda:
5*z = 4*x + y - 10, restas 4*x, restas y, sumas 10 en ambos miembros, y queda:
-4*x - y + 5*z + 10 = 0,
que es una ecuación cartesiana implícita del plano tangente a la gráfica de la función definida implícitamente por la ecuación de tu enunciado, en el punto de contacto A.
Espero haberte ayudado.
-
Buenas, cual es la región de convergencia de la serie de potencias (x^2n)/(4^n). Yo creo que es infinito, pero no estoy seguro...


Antonio Silvio Palmitano
el 4/1/20Planteas la razón del término general siguiente entre el término general, y queda:
an+1/an = (x2(n+1)/4n+1) / (x2n/4n) = simplificas = x2/4.
Luego, aplicas el Criterio de la razón, y queda:
Lím(n→+∞) (an+1/an) = Lím(n→+∞) (x2/4) = (x2/4)*Lím(n→+∞) (1) = x2/4,
y tienes tres opciones:
1°)
Lím(n→+∞) (an+1/an) < 1, de donde tienes: x2/4 < 1, que corresponde a: |x| < 2, en el que la serie es convergente;
2°)
Lím(n→+∞) (an+1/an) > 1, de donde tienes: x2/4 > 1, que corresponde a: |x| > 2, en el que la serie es divergente;
3°)
Lím(n→+∞) (an+1/an) = 1, de donde tienes: x2/4 = 1, que corresponde a: |x| = 2, en el que tienes dos opciones:
a)
x = 2, para el cuál el término general de la serie queda: an = 22n/4n = (22)n/4n = 4n/4n = 1,
que corresponde a una serie constante, por lo tanto divergente,
b)
x = -2, para el cuál el término general de la serie queda: an = (-2)2n/4n = ([-2]2)n/4n = 4n/4n = 1,
que corresponde a una serie constante, por lo tanto divergente.
Luego, puedes concluir que la condición de convergencia de la serie es: |x| < 2, que corresponde al intervalo de convergencia: Ic = (-2;2).
Espero haberte ayudado.
-
Buenas, la pregunta es si la siguiente sucesión es convergente o divergente.Yo creo que es divergente (pero me gustaría comprobarlo).
Σ [3*ln(n)]/[2*n^2]
lo que yo he hecho es comparar con 1/n (divergente). Al hacer el límite cuando n tiende a infinito de la razón de [3*ln(n)]/[2*n^2] entre 1/n nos da infinito, por lo que el "criterio del cociente" nos dice que si el denominador (1/n) es divergente (lo es), el numerador también lo será. De todas maneras me gustaría comprobarlo.
Muchas gracias.

Breaking Vlad
el 8/1/20Hola! Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-


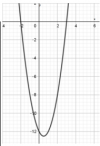
Jose Ramos
el 4/1/20y = ax2 + bx + c. El término lineal es bx Para hallar b, partes de lo siguiente: c = f(0) = -12. Por otra parte si x1 y x2 son las raíces del polinomio, se sabe que x1.x2 = c/a, de donde -2.3 = -12/a de donde a = 2. Por último x1+x2 = -b/a, de donde -2+3 = -b/2 , de donde b =2. El polinomio que expresa la función de la gráfica es 2x2 + 2x -12 y su término lineal es 2x.