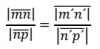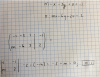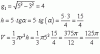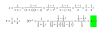-
Hola.
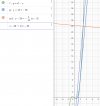
Buenas noches, estoy repasando haciendo ejercicios sobre adivinar la ecuación de la recta tangente. Bueno y haciendo ejercicios no se como se realiza este, si me lo pudiera hacer, se lo agradecería mucho.
Gracias por su atención me ayudáis mucho a la hora de estudiar.
Una cosa si me lo pudiera representar por gráfica también se lo agradecería sino le es molestia porque así me entero aún más.
Le envió la foto:
-
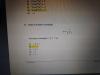
Me ayudan? Para que me quede más claro, por favor. Saqué la ecuación haciendo el sistema, y cuando lo intento por el producto vectorial me da un vector con otras coordenadas, a ese vector lo podría dividir entre 2 para obtener lo mismo? Y para el punto que me falta puedo hacer 0 cualquier variable y que me salga lo mismo que en el sistema?



Antonio
el 3/1/20Lo tienes bien resuelto!!!!!
La intersección de los dos planos es una recta cuya ecuación es la que obtuviste.
Si las coordenadas de un vector se dividen o se multiplican por un mismo número (distinto de cero) se obtiene un vector distinto pero cuya dirección es la misma que el primero, es decir, a tu pregunta comentarte que sí, da lo mismo usar uno que otro.
Un punto de la recta es P(1,0,0) y el vector director de la misma v→(-1,0,1)
-
Me podrían ayudar, que no se supone que al hacer el producto vectorial de los normales a los planos me tendría que dar lo mismo que cuando resolví el sistema para hallar la intersección?



Jose Ramos
el 3/1/20z no es 0. Cuando tienes x = t/2 e y = t, has de despejar z de una de las dos ecuaciones, por ejemplo de la segunda, se deduce z = x - 3y = t/2 - 3t = -5/2 t. El resultado final es la recta cuyo vector es (1/2, 1, -5/2) que como dirección es igual al vector (1, 2, -5) que es el que obtienes tú en el producto vectorial de los normales a los planos.
-


Antonio Silvio Palmitano
el 3/1/20Vamos con una orientación.
En la primera fracción:
considera el numerador, observa que es una trinomio cuadrado perfecto, que al factorizar queda: (x - 3)2,
considera el denominador, observa que es un polinomio cuadrático, que al factorizar queda: (x - 3)*(x + 5);
luego, sustituyes expresiones, y la primera fracción queda:
(x - 3)2/[(x - 3)*(x + 5)] = simplificas = (x - 3)/(x + 5) (1).
En la segunda fracción:
considera el numerador, observa que puedes extraer factor común numérico, que al factorizar queda: 2*(x - 5),
considera el denominador, observa que es una resta de cuadrados perfectos, que al factorizar queda: (x - 5)*(x + 5);
luego, sustituyes expresiones, y la primera fracción queda:
2*(x - 5)/[(x - 5)*(x + 5)] = simplificas = 2/(x + 5) (2).
Luego, sustituyes las expresión señalada (1) en lugar de la primera fracción de tu enunciado, sustituyes la expresión señalada (2) en lugar de la segunda fracción de tu enunciado, y queda:
(x - 3)/(x - 5) : 2/(x - 5) = simplificas denominadores = (x - 3) : 2 = resuelves = (x - 3)/2,
por lo que puedes concluir que la opción señalada (C) es la respuesta correcta.
Espero haberte ayudado.