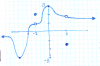
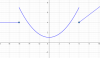
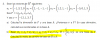-
-


Breaking Vlad
el 8/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
Felices Reyes a todos.
Estimado profe, creo que hay un error en el enunciado de uno de los ejercicios propuestos. Pone 3,5 elevado a x igual a 75. Podrías confirmar que ese enunciado es correcto por favor?/ Grcs.
-
Sigo sin entender el problema:
Determinar el desarrollo en serie de potencias de la función: f(x)=x*sen(x) + cos(x)
Sé hacer el desarrollo de Maclaurin (y de Taylor) de la función x, de sen(x) y de cos(x). Pero una vez que los tengo hechos, no sé qué hacer. ¿Cuál es el siguiente pasO? Se me ocurre que en vez de hacer el desarrollo de x (por un lado), el seno de x (por otro lado) y finalmente el coseno de x (por otro lado) debería hacerlo todo junto. Pero no sé la verdad...


Antonio Silvio Palmitano
el 6/1/20Planteas los desarrollos de Mc Laurin para la función seno y para la función coseno (te dejo la tarea), y queda:
senx = ∑(k = 0,+∞) ([-1]k/[2k+1]!)*x2k+1 (1),
cosx = ∑(h = 0,+∞) ([-1]h/[2h]!)*x2h = extraes el primer término = 1 + ∑(h = 1,+∞) ([-1]h/[2h]!)*x2h = 1 + ∑(h = 1,+∞) ([-1]h-1*(-1)/[2h]!)*x2h (2).
Luego, planteas la expresión del primer término de la función cuya expresión tienes en tu enunciado, y queda:
x*senx = sustituyes la expresión señalada (1), y queda:
= x*∑(k = 0,+∞) ([-1]k/[2k+1]!)*x2k+1 = introduces el factor (x) en la suma infinita, resuelves su argumento, y queda:
= ∑(k = 0,+∞) ([-1]k/[2k+1]!)*x2k+2 = extraes factor común en el exponente del factor literal, y queda:
= ∑(k = 0,+∞) ([-1]k/[2k+1]!)*x2(k+1) = aplicas el cambio de índice: h = k + 1, y queda:
= ∑(h = 1,+∞) ([-1]h-1/[2h-1]!)*x2h (3).
Luego, tienes la expresión de la función de tu enunciado:
f(x) = x*senx + cosx =
sustituyes la expresión señalada (3) en el primer término, sustituyes la expresión señalada (2) en el segundo término, y queda:
= ∑(h = 1,+∞) ([-1]h-1/[2h-1]!)*x2h + 1 + ∑(h = 1,+∞) ([-1]h-1*(-1)/[2h]!)*x2h =
ordenas términos, y queda:
= 1 + ∑(h = 1,+∞) ([-1]h-1/[2h-1]!)*x2h + ∑(h = 1,+∞) ([-1]h-1*(-1)/[2h]!)*x2h =
asocias las sumas infinitas (observa que extraemos factores comunes en el argumento), y queda:
= 1 + ∑(h = 1,+∞) ( [-1]h-1*( 1/[2h-1]! -1/[2h]! )*x2h =
resuelves el coeficiente en el término general de la suma, y queda:
= 1 + ∑(h = 1,+∞) ( [-1]h-1*( [2h-1]/[2h]! )*x2h =
introduces el término constante en la suma (observa: 1 = [-1]0-1*( [2*0-1]/[2*0]!), y queda:
= ∑(h = 0,+∞) ( [-1]h-1*( [2h-1]/[2h]! )*x2h.
Espero haberte ayudado.