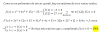¡UPS! Para ver vídeos en la web debes estar registrado, es totalmente gratuito.
Recuerda además que sólo por ser unicoo, GRATIS, podrás dejar tus dudas en los foros de beUnicoos, acumularás energy y help points y ganarás decenas de medallas. Registrarte solo te llevará unos segundos. Nosotros somos unicoos ¿y tú? #nosvemosenclase
Teorema de Bolzano-Rolle - Única raiz de una función
Correspondiente a 2º de BACHILLER, demostraremos que dos funciones f(x) y g(x) tienen un unico punto de corte en el intervalo (0,1). Es el mismo proceso que para demostrar que una ecuación tiene una unica solución. Para ello, primero aplicaremos el TEOREMA DE BOLZANO, para demostrar que la ecuación tiene al menos una solución. Partiremos entonces del supuesto de que hay más de una, y aplicando el TEOREMA de ROLLE, comprobaremos que esa suposición es absurda, de modo que quedará demostrado que tiene una sola raiz. Por esa razón, muchos profesores llamamos a este tipo de ejercicios, aplicación del teorema de "ROLLZANO"...
* Para utilizar tu mochila o guardar tu progreso y acumular energy points debes ser usuario registrado. Regístrate o inicia sesión
Material adicional
* Los materiales marcados con el símbolo de la estrella () sólo serán accesibles para usuarios PRO. Conviértete en PRO
Foro de preguntas y respuestas
-
Hola Profe, muchas gracias por todos los videos. Tengo una duda el Teorema di Rolle-Bolzano solamente nos sirve para demostrar que existe un solo punto de corte o también de manera contraria podemos demostrar que existe más de un corte.
Muchas gracias.