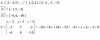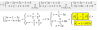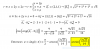¡UPS! Para ver vídeos en la web debes estar registrado, es totalmente gratuito.
Recuerda además que sólo por ser unicoo, GRATIS, podrás dejar tus dudas en los foros de beUnicoos, acumularás energy y help points y ganarás decenas de medallas. Registrarte solo te llevará unos segundos. Nosotros somos unicoos ¿y tú? #nosvemosenclase
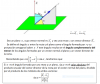
Vector director y punto de una recta dada como intersección de dos planos
Correspondiente a GEOMETRÍA EN EL ESPACIO de Bachillerato, a partir de la ecuación de una recta dada como intersección de dos planos, obtendremos un vector director y un punto de la recta, resolviendo el sistema compatible indeterminado que conforman ambas ecuaciones.
* Para utilizar tu mochila o guardar tu progreso y acumular energy points debes ser usuario registrado. Regístrate o inicia sesión
Material adicional
* Los materiales marcados con el símbolo de la estrella () sólo serán accesibles para usuarios PRO. Conviértete en PRO
Foro de preguntas y respuestas
-
Muchas gracias por el vídeo, he entendido todo en unos minutos lo que hemos dado semanas. Pero me ha surgido una duda, entonces para sacar el punto y el vector director hay que hacerlo con la ecuación paramétrica o se puede de otro modo? Gracias de antemano
-
Hola buenos días queria preguntarles si es posible que en el ejercicio 8 de este tema haya un error al realizar gauss en el número -3a-5 porque a mi me sale -4a+5 y no entiendo si me estoy equivocando yo o es que esta errado.
Gracias
-
Profesor si me puede ayudar con este ejercicio:
Dados los puntos A(1,1,1) ;B ( 2,-3,5) ; C ( 1,2,2) D(-4 , 3 ,-5)hallar: a) ecuación del plano BCD. b) Distancia del punto A al plano BCD. c) ecuaciones de la recta q pasa por a y es perpendicular al plano BCD
-
Bueno profesor agradecerle ante todo por su ayuda pero aquí viene el verdadero reto... Y el problema es el siguiente:
obtener un punto A de la recta r y un vector que tenga su dirección donde:
r={3x-2y+5z-3=0 ; x+y-z+1=0
-
Buenas tardes profesor (a) quería saber si me podía ayudar con un problema me preparo para el examen de selectividad para extranjeros y mi problema es la siguiente... hallar el ángulo de la recta x =2y=2z con el plano 3x+2y+z=0