-


Antonio Silvio Palmitano
el 18/1/20Puedes comenzar por establecer un sistema de referencia con eje OX horizontal con sentido positivo hacia la derecha según tu figura, y con eje OY vertical con sentido positivo hacia arriba.
Luego, tienes que sobre el bloque de la izquierda, cuya masa es: Mi = 15 Kg, están aplicadas cuatro fuerzas, de las que indicamos sus módulos, direcciones y sentidos:
Peso: Pi = Mi*g, vertical hacia abajo,
Acción normal de la superficie de apoyo: Ni, vertical hacia arriba,
Tensión de la cuerda: T, horizontal hacia la derecha,
Rozamiento dinámico de la superficie de apoyo: frdi = μd*Ni, horizontal hacia la izquierda;
luego, aplicas la Segunda Ley de Newton, y tienes las ecuaciones:
T - frdi = Mi*a,
Ni - Pi = 0,
sustituyes las expresiones de los módulos de las fuerzas, y queda:
T - μd*Ni = Mi*a,
Ni - Mi*g = 0, de aquí despejas: Ni = Mi*g (1),
sustituyes la expresión remarcada y señalada (1) en la primera ecuación, y queda:
T - μd*Mi*g = Mi*a, de aquí despejas: T = μd*Mi*g + Mi*a (2).
Luego, tienes que sobre el bloque de la derecha, cuya masa es: Md = 20 Kg, están aplicadas cinco fuerzas, de las que indicamos sus módulos, direcciones y sentidos:
Peso: Pd = Md*g, vertical hacia abajo,
Acción normal de la superficie de apoyo: Nd, vertical hacia arriba,
Tensión de la cuerda: T, horizontal hacia la izquierda,
Rozamiento dinámico de la superficie de apoyo: frdd = μd*Nd, horizontal hacia la izquierda,
Fuerza externa: F, horizontal hacia la derecha;
luego, aplicas la Segunda Ley de Newton, y tienes las ecuaciones:
F - T - frdd = Mi*a,
Nd - Pd = 0,
sustituyes las expresiones de los módulos de las fuerzas, y queda:
F - T - μd*Nd = Md*a,
Nd - Md*g = 0, de aquí despejas: Nd = Md*g (3),
sustituyes la expresión remarcada y señalada (3) en la primera ecuación, y queda:
F - T - μd*Md*g = Mi*a, de aquí despejas: T = F - μd*Md*g - Md*a (4).
Luego, sustituyes la expresión señalada (2) en el primer miembro de la ecuación señalada (4), y queda:
μd*Mi*g + Mi*a = F - μd*Md*g - Md*a, sumas Md*a y restas μd*Mi*g en ambos miembros, y queda:
Mi*a + Md*a = F - μd*Mi*g - μd*Md*g,
extraes factor común en el primer miembro, extraes factores comunes en los dos últimos términos del segundo miembro, y queda:
(Mi + Md)*a = F - μd*(Mi + Md)*g, divides por (Mi + Md) en ambos miembros, y queda:
a = [F - μd*(Mi + Md)*g]/(Mi + Md) (5),
que es la expresión de la aceleración de los bloques en función de los datos de tu enunciado;
luego, sustituyes la expresión remarcada y señalada (5) en la ecuación señalada (2) o en la ecuación señalada (4) (nosotros elegimos la primera de ellas), y queda:
T = μd*Mi*g + Mi*[F - μd*(Mi + Md)*g]/(Mi + Md) (6),
que es la expresión del módulo de la tensión de la cuerda en función de los datos de tu enunciado.
Luego, queda que reemplaces valores en las ecuaciones remarcadas y señaladas (5) (6) y hagas los cálculos.
Espero haberte ayudado.
-
El observa que el tiempo que tarda un oscilador armónico en pasar de su posición de equilibrio a la del desplazamiento máximo con relación a está es de 3/2 segundos¿Cuál es su periodo?
-
 Tengo dudas en el siguiente problema:
Tengo dudas en el siguiente problema:Una onda armónica transversal se propaga por una cuerda tensa de gran longitud, y por ello, una partícula de la misma realiza un movimiento armónico simple en dirección perpendicular a la cuerda. El periodo de dicho movimiento es 3s y la distancia que recorre la partícula entre dos posiciones extremas es 20cm.
a) Valores de la velocidad máxima y de la aceleración máxima de oscilación de la partícula
b) Si la distancia mínima que separa dos partículas de la cuerda que oscilan en fase es 60cm, ¿Cual será la velocidad de propagación de la onda? ¿Cual será el número de onda?
No se si lo tengo bien resuelto, si me lo pueden revisar y decirme si tengo algún fallo para poder corregirlo por favor.


Antonio Silvio Palmitano
el 19/1/20Tienes el periodo de oscilación:
T = 3 s, con este valor, planteas la expresión del coeficiente angular, y queda:
ω = 2π/T = 2π/3 rad/s.
Luego, recuerda que la distancia entre dos posiciones extremas es igual al doble de la amplitud de oscilación del punto en estudio, por lo que tienes:
A = (20 cm)/2 = 10 cm = 0,1 m,
que es la amplitud de oscilación del punto en estudio.
Luego, recuerda que la distancia mínima entre dos puntos que oscilan en fase es igual a la longitud de onda, por lo que tienes:
λ = 60 cm = 0,6 m, con este valor planteas la expresión del número de onda, y queda:
N = 2π/λ = 2π/0,6 = 10π/3 rad/m.
Luego, planteas la expresión de la función de onda, y queda:
y(t,x) = A*sen(ω*t - N*x + φ), reemplazas valores que tienes calculados, y queda:
y(t,x) = 0,1*sen( [2π/3]*t - [10π/3]*x + φ ) (1).
a)
Considera un punto fijo de la onda, por ejemplo el que corresponde a la posición: x = 0, reemplazas este valor en la expresión de la función de onda señalada (1), resuelves el argumento del seno, y queda:
y(t,0) = 0,1*sen( [2π/3]*t + φ ),
derivas con respecto al tiempo, y queda:
vy(t,0) = 0,1*2π/3*cos( [2π/3]*t + φ ), resuelves el coeficiente, y queda:
vy(t,0) = [π/15]*cos( [2π/3]*t + φ ) (2), que es la expresión de la velocidad del punto en estudio en función del tiempo,
y el valor absoluto de su coeficiente es la amplitud de velocidad, por lo que tienes que la rapidez máxima del punto en estudio queda expresada:
vyM = π/15 m/s;
luego, derivas con respecto al tiempo la expresión de la función velocidad señalada (2), y queda:
ay(t,0) = -[2π2/45]*sen( [2π/3]*t + φ ), que es la expresión de la aceleración del punto en estudio en función del tiempo,
y el valor absoluto de su coeficiente es la amplitud de aceleración, por lo que tienes que la aceleración máxima del punto en estudio queda expresada:
ayM = 2π2/45 m/s2.
b)
Planteas la expresión de la rapidez de propagación en función de la longitud de onda y del periodo de oscilación, y queda:
v = λ/T, reemplazas valores, y queda:
v = 0,6/3, resuelves, y queda:
v = 0,2 m/s.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 18/1/20Vamos con un planteo vectorial para este problema.
Consideramos que la arista cuya longitud tienes señalada "3a" se encuentra en el eje OX, que la arista cuya longitud tienes señalada "4a" se encuentra en el eje OY, y que la arista cuya longitud tienes señalada "a" se encuentra en el eje OZ.
Luego, observa que los vértices de la cuña son:
O(0,0,0), A(3a,0,0), B(0,4a,0), C(0,0,a), D(3a,4a,0) y E(0,4a,a),
y observa también que la cuña tiene cinco caras, tres de ellas rectangulares y dos de ellas triangulares, a la que consideraremos por separado.
1°)
Cara rectangular OABD incluida en el plano OXY, para la que puedes definir los vectores:
u1 = OA = < 3a ; 0 ; 0 >,
u2 = OB = < 0 ; 4a ; 0 >,
planteas la expresión del producto vectorial de estos dos vectores, y queda:
u1 x u2 = < 3a ; 0 ; 0 > x < 0 ; 4a ; 0 > = < 0 ; 0 ; 12a2 >,
cuyo módulo queda expresado:
|u1 x u2| = 12a2;
luego, aplicas la propiedad del módulo del producto vectorial entre ambos vectores (recuerda que es igual al área del paralelogramo determinado por ellos), y queda:
AOABD = |u1 x u2| = 12a2.
2°)
Cara rectangular OBCE incluida en el plano OYZ, para la que puedes definir los vectores:
v1 = OB = < 0 ; 4a ; 0 >,
v2 = OC = < 0 ; 0 ; a >,
planteas la expresión del producto vectorial de estos dos vectores, y queda:
v1 x v2 = < 0 ; 4a ; 0 > x < 0 ; 0 ; a > = < 4a2 , 0 ; 0 >,
cuyo módulo queda expresado:
|v1 x v2| = 4a2;
luego, aplicas la propiedad del módulo del producto vectorial entre ambos vectores (recuerda que es igual al área del paralelogramo determinado por ellos), y queda:
AOBCE = |v1 x v2| = 4a2.
3°)
Cara rectangular ACDE incluida en un plano paralelo al eje OY, para la que puedes definir los vectores:
w1 = AC = < -3a ; 0 ; a >,
w2 = AD = < 0 ; 4a ; 0 >,
planteas la expresión del producto vectorial de estos dos vectores, y queda:
w1 x w2 = < -3a ; 0 ; a > x < 0 ; 4a ; 0 > = < -4a2 , 0 ; -12a2 >,
cuyo módulo queda expresado:
|w1 x w2| = √(160)a2 = 4√(10)a2:
luego, aplicas la propiedad del módulo del producto vectorial entre ambos vectores (recuerda que es igual al área del paralelogramo determinado por ellos), y queda:
AACDE = |w1 x w2| = 4√(10)a2.
4°)
Cara triangular OAC incluida en el plano OXZ, para la que puedes definir los vectores:
r1 = OA = < 3a ; 0 ; 0 >,
r2 = OC = < 0 ; 0 ; a >,
planteas la expresión del producto vectorial de estos dos vectores, y queda:
r1 x r2 = < 3a ; 0 ; 0 > x < 0 ; 0 ; a > = < 0 ; -3a2 ; 0 >,
cuyo módulo queda expresado:
|r1 x r2| = 3a2;
luego, aplicas la propiedad del módulo del producto vectorial entre ambos vectores (recuerda que es igual al doble del área del triángulo determinado por ellos), y queda:
AOAC = (1/2)*|r1 x r2| = (3/2)a2.
5°)
Cara triangular BDE incluida en u plano paralelo al plano OXZ, para la que puedes definir los vectores:
s1 = BD = < 3a ; 0 ; 0 >,
s2 = BE = < 0 ; 0 ; a >,
planteas la expresión del producto vectorial de estos dos vectores, y queda:
s1 x s2 = < 3a ; 0 ; 0 > x < 0 ; 0 ; a > = < 0 ; -3a2 ; 0 >,
cuyo módulo queda expresado:
|s1 x s2| = 3a2;
luego, aplicas la propiedad del módulo del producto vectorial entre ambos vectores (recuerda que es igual al doble del área del triángulo determinado por ellos), y queda:
ABDE = (1/2)*|s1 x s2| = (3/2)a2.
Luego, planteas la expresión del área lateral total de la cuña como la suma de las áreas de sus cinco caras, y queda:
A = 12a2 + 4a2 + 4√(10)a2 + (3/2)a2 + (3/2)a2, reduces términos con coeficientes racionales, y queda:
A = 19a2 + 4√(10)a2, extraes factor común, y queda:
A = [19 + 4√(10)]a2.
Espero haberte ayudado.
-
Buenas noches . Ayuda por favor estoy en el cole y tengo que estudiar áreas y volúmenes de figuras en el espacio vectorialmente. No se cómo se saca el area de una cuña o prisma porfa alguien
-
Hola, buenas. Me pierdo en la parte de descomponer las fuerzas de los 2 cuadrados. A los 2 les puse que de arriba hacia abajo son N y P(Y). El problema viene cuando hay que poner las P(x) y las FR. Tampoco tengo muy claro como plantear el sumatorio de furzas de ambos cuerpos.


Antonio Silvio Palmitano
el 17/1/20Comienza por considerar cada bloque por separado.
Para el bloque de la izquierda.
Establece un sistema de referencia con eje OX paralelo a la rampa de la izquierda con sentido positivo hacia arriba, y con eje OY perpendicular a dicha rampa con sentido positivo hacia arriba;
luego, observa que sobre este bloque están aplicadas cuatro fuerzas, de las que indicamos sus módulos, direcciones y sentidos:
Peso: P1 = M1*g, vertical hacia abajo,
Acción normal de la rampa: N1, perpendicular a la rampa hacia arriba,
Rozamiento dinámico de la rampa: frd1 = μd*N1, paralela a la rampa, hacia abajo,
Tensión de la cuerda: T, paralela a la rampa, hacia arriba;
luego, aplicas la Segunda Ley de Newton, y quedan las ecuaciones (observa que sustituimos las expresiones de los módulos de las fuerzas):
T - M1*g*senθ - μd*N1 = M1*a,
N1 - M1*g*cosθ = 0, de aquí despejas: N1 = M1*g*cosθ (1),
sustituyes la expresión señalada (1) en el tercer término de la primera ecuación, y queda:
T - M1*g*senθ - μd*M1*g*cosθ = M1*a, de aquí despejas: T = M1*g*senθ + μd*M1*g*cosθ + M1*a (2).
Para el bloque de la derecha.
Establece un sistema de referencia con eje OX paralelo a la rampa de la derecha con sentido positivo hacia abajo, y con eje OY perpendicular a dicha rampa con sentido positivo hacia arriba;
luego, observa que sobre este bloque están aplicadas cuatro fuerzas, de las que indicamos sus módulos, direcciones y sentidos:
Peso: P2 = M2*g, vertical hacia abajo,
Acción normal de la rampa: N2, perpendicular a la rampa hacia arriba,
Rozamiento dinámico de la rampa: frd2 = μd*N2, paralela a la rampa, hacia arriba,
Tensión de la cuerda: T, paralela a la rampa, hacia arriba;
luego, aplicas la Segunda Ley de Newton, y quedan las ecuaciones (observa que sustituimos las expresiones de los módulos de las fuerzas):
M2*g*senθ - μd*N2 - T = M2*a,
N2 - M2*g*cosθ = 0, de aquí despejas: N2 = M2*g*cosθ (3),
sustituyes la expresión señalada (3) en el segundo término de la primera ecuación, y queda:
M2*g*senθ - μd*M2*g*cosθ - T = M2*a (4).
Luego, reemplazas datos (M1 = 3 Kg, M2 = 6 Kg, θ = 30°, g = 9,8 m/s2, a = 1 m/s2) en las ecuaciones señaladas (2) (4), resuelves coeficientes, y queda el sistema de ecuaciones:
T ≅ 14,7 + μd*25,461 + 3 (2*),
29,4 - μd*50,922 - T ≅ 6 (4*);
luego, sustituyes la expresión señalada (2*) en la ecuación señalada (4*), distribuyes su tercer término, y queda:
29,4 - μd*50,922 - 14,7 - μd*25,461 - 3 ≅ 6, reduces términos semejantes en el primer miembro, y queda:
11,7 - μd*76,383 ≅ 6, restas 11,7 y luego divides por 76,383 en ambos miembros, y queda:
μd ≅ 0,075;
luego, reemplazas este valor remarcado en la ecuación señalada (2*), resuelves, y queda:
T ≅ 19,610 N;
luego, puedes reemplazar datos en las ecuaciones señaladas (1) (3) y podrás calcular los módulos de las acciones normales que las rampas ejercen sobre los cuerpos que deslizan sobre ellas.
Espero haberte ayudado.
-
 Tengo dudas en el siguiente problema:
Tengo dudas en el siguiente problema:Un objeto se mueve en el plano XY, con movimiento MRUA en el eje x y una aceleración de 1,2m/s2 y un MRU en el eje y con velocidad 2,8m/s. En el instante t=0 se encuentra en (r= 2i - j) y al cabo de t1s se ha desplazado a la posición (r= -4i + 6j)
a) Determina t1
b) Determina el vector velocidad (vo)
c) Hallar los vectores posición y velocidad en el instante cualquiera t
No sé si hay que cambiar las condiciones de movimiento, en el caso del eje y decir que vy=voy=2,8m/s y en el eje x, aunque me de la aceleración (1,2m/s2), como es un MRUA y se mueve en el eje horizontal, la a=0, no se si será así. El planteamiento lo hice así pero no sé si es correcto o no, por si me puede ayudar por favor.


Antonio Silvio Palmitano
el 17/1/20Tienes la expresión vectorial de la posición inicial del móvil:
ri = < 2 ; -1 > m (1), que corresponde al instante inicial: ti = 0, cuyas componentes son: xi = 2 m, yi = -1 m.
Tienes la expresión vectorial de la posición final del móvil:
rf = < -4 ; 6 > m (2), que corresponde al instante final: tf = t1, cuyas componentes son: xf = -4 m, yf = 6 m.
a)
Planteas la ecuación de posición de Movimiento Rectilíneo Uniforma para las componentes en la dirección del eje OY (observa que tienes la expresión de la velocidad: vy = 2,8 m/s), y queda:
yf = yi + vy*(t - ti), sustituyes las expresiones de los datos, y queda:
6 = -1 + 2,8*(t1 - 0), y de aquí despejas:
tf = 2,5 s.
b)
Planteas la ecuación de posición de Movimiento Rectilíneo Uniformemente Variado para las componentes en la dirección del eje OX (observa que tiens la expresión de la aceleración: ax = 1,2 m/s), y queda:
xf = xi + vxi*(tf - ti) + (1/2)*ax*(tf - ti)2, reemplazas los valores de los datos y el valor del instante final que tienes remarcado, y queda:
-4 = 2 + vxi*(2,5 - 0) + (1/2)*1,2*(2,5 - 0i)2, resuelves términos y coeficientes, y queda:
-4 = 2 + vxi*2,5 + 3,75, reduces términos semejantes en el segundo miembro, y queda:
-4 = 5,75 + vxi*2,5, y de aquí despejas:
vxi = -3,9 m/s;
luego, planteas la ecuación de velocidad de Movimiento Rectilíneo Uniformemente Variado para las componentes en la dirección del eje OX, y queda:
vx = vxi + ax*(t - ti), reemplazas los valores iniciales y el valor de la aceleración, y queda:
vx = -3,9 + 1,2*(t - 0), cancelas el término nulo en el agrupamiento, resuelves el último término, y queda:
vx = -3,9 + 1,2*t (en m/s), que es la expresión general de la componente de la velocidad en la dirección del eje OY;
luego, con el valor de la componente de la velocidad en la dirección del eje OY que tienes en tu enunciado, y con esta última expresión remarcada, planteas la expresión vectorial de la función velocidad del móvil, y queda:
v(t) = < -3,9+1,2*t ; 2,8 > m/s.
c)
Planteas las expresiones de las componentes del vector posición, y queda:
x = xi + vxi*(t - ti) + (1/2)*ax*(t - ti)2,
y = yi + vy*(t - ti),
reemplazas datos y valores que tienes calculados, cancelas términos nulos, resuelves coeficientes, y queda:
x = 2 - 3,9*t + 0,6*t2 (en m),
y = -1 + 2,8*t (en m);
luego, con estas dos últimas expresiones, planteas la expresión vectorial de la función posición del móvil, y queda:
r(t) = < 2-3,9*t+0,6*t2 ; -1+2,8*t > m.
Espero haberte ayudado.
-
 Tengo dudas en el siguiente problema:
Tengo dudas en el siguiente problema:Dentro de un depósito elevado cerrado el agua alcanza una altura de 10 m. Sobre la superficie del agua hay aire a una presión manométrica de 4.2 kPa. De una de las paredes laterales y justamente encima del fondo, sale una tubería horizontal de 450 cm2 de sección que se estrecha hasta que dicha sección es 225 cm2. Esta tubería está abierta y por ella sale el agua continuamente. a) Calcular el caudal (en L/s) que fluye a través de la tubería. b) ¿Cuál es la presión manométrica en la parte ancha de la tubería? Suponer que el flujo es laminar y no viscoso.
No no sé cómo calcular el caudal y la presión si tengo dos tuberías que están juntas y tienen diferente sección y presión a la vez. Si me pueden explicar como poder resolverlo por favor, el planteamiento al que he llegado es el que tengo en la foto.


Antonio Silvio Palmitano
el 17/1/20Puedes designar con A a un punto ubicado en la superficie de líquido, B a un punto ubicado en el tramo grueso de la tubería, y C a un punto ubicado en el tramo estrecho de la tubería.
Luego, establece un sistema de referencia con origen de coordenadas a nivel del fondo del depósito, y con eje OY vertical con sentido positivo hacia arriba.
Luego, tienes los datos para el punto A (observa que consideramos que el nivel de líquido desciende muy lentamente):
pA = Patm + PmA,
yA = 10 m,
vA ≅ 0.
Luego, tienes los datos para el punto B:
pB = a determinar,
yB = 0,
vB = a determinar,
AB = 450 cm2 = 0,045 m2.
Luego, tienes los datos para el punto C (observa que este tramo está abierto a la atmósfera):
pC = Patm,
yC = 0,
vC = a determinar,
AC = 225 cm2 = 0,0225 m2.
Luego, planteas la ecuación de Bernoulli entre los puntos A y B, y entre los puntos A y C, y quedan las ecuaciones:
pA + δL*g*yA + (1/2)*δL*vA2 = pB + δL*g*yB + (1/2)*δL*vB2,
pA + δL*g*yA + (1/2)*δL*vA2 = pC + δL*g*yC + (1/2)*δL*vC2,
sustituyes la expresión de la presión en el punto A, y también en el punto C, cancelas términos con factores nulos, y queda:
Patm + PmA + δL*g*yA = pB + (1/2)*δL*vB2,
Patm + PmA + δL*g*yA = Patm + (1/2)*δL*vC2,
mantienes la primera ecuación, restas en ambos miembros de la segunda ecuación, y queda:
Patm + PmA + δL*g*yA = pB + (1/2)*δL*vB2 (1),
PmA + δL*g*yA = (1/2)*δL*vC2, de aquí despejas: vC = √(2*[PmA + δL*g*yA]/δL) = √(2*[4200 + 1000*9,8*10]/1000) = √(204,4) m/s ≅ 14,297 m/s.
Luego, planteas la expresión del caudal en el tramo estrecho de la tubería, y queda:
Q = AC*vC = 0,0225*√(204,4) m3/s ≅ 0,322 m3/s (a),
que es el caudal en el tramo grueso de la tubería, ya que consideramos que el líquido es incompresible.
Luego, planteas la expresión del caudal en el tramo grueso de la tubería, y queda:
Q = AB*vB, divides por AB en ambos miembro, y luego despejas:
vB = Q/AB = 0,0225*√(204,4)/0,045 = 0,5*√(204,4) m/s ≅ 7,148 m/s.
Luego, restas y restas en ambos miembros de la ecuación señalada (1), y luego despejas:
pB - Patm = PmA + δL*g*yA - (1/2)*δL*vB2, sustituyes la expresión de la presión manométrica en el punto B en el primer miembro, y queda:
PmB = PmA + δL*g*yA - (1/2)*δL*vB2, reemplazas datos y valores que tienes calculados, y queda:
PmB = 4200 + 1000*9,8*10 - (1/2)*1000*[0,5*√(204,4)]2 = 4200 + 98000 - 25550 = 76650 Pa = 76,65 KPa (b).
Espero haberte ayudado.
-
Buenas noches. Necesito me ayuden a resolver el problema uno de la guía. Por favor. O que me den alguna recomendación. Por favor. Gracias. 
Un cuerpo de masa m tiene una velocidad de 5 m/s en la parte más baja de un plano inclinado (α = 30 ◦) calcular la distancia x a la que cae al suelo si la altura de la rampa es de 1 m (ver dibujo).


Antonio Silvio Palmitano
el 17/1/20Puedes plantear el problema en dos etapas, la primera es el ascenso del cuerpo por la rampa hasta que alcanza su punto más alto, y la segunda es el movimiento del cuerpo en un plano vertical, y observa que los datos finales de la primera etapa son útiles para establecer los datos iniciales de la segunda.
1°)
Considera un sistema de referencia con origen en el pie de la rampa, con eje OX horizontal con sentido positivo hacia la derecha según tu figura, y con eje OY vertical con sentido positivo hacia arriba.
Luego, planteas la expresión de la energía mecánica inicial del cuerpo, y queda:
EMi = EPi + ECi = M*g*yi + (1/2)*M*vi2 = M*9,8*0 + (1/2)*M*52 = 0 + 12,5*M = 12,5*M (1) (en Joules).
Luego, planteas la expresión de la energía mecánica final del cuerpo, y queda:
EM1 = EP1 + EC1 = M*g*y1 + (1/2)*M*v12 = M*9,8*1 + (1/2)*M*v12 = 9,8*M + (1/2)*M*v12 (2) (en Joules).
Luego, planteas conservación de la energía mecánica, y queda la ecuación:
EM1 = EMi, sustituyes las expresiones señaladas (2) (1), y queda:
9,8*M + (1/2)*M*v12 = 12,5*M, divides por M en todos los términos, y queda:
9,8 + (1/2)*v12 = 12,5, restas 9,8 en ambos miembros, luego multiplicas por 2 en ambos miembros, y queda:
v12 = 5,4, extraes raíz cuadrada positiva en ambos miembros, y queda:
v1 = √(5,4) m/s ≅ 2,324 m/s, que es el valor del módulo de la velocidad del cuerpo cuando alcanza el punto más alto de la rampa,
y observa que la dirección de la velocidad es la que le imprime la rampa, por lo que tienes que la velocidad del cuerpo en ese punto forma un ángulo: α = 30° con respecto al semieje OX positivo.
2°)
Considera un sistema de referencia con eje OX horizontal con sentido positivo hacia la derecha, con eje OY vertical con sentido positivo hacia arriba y que pase por el punto más alto de la rampa, por lo que tienes que el origen de coordenadas es su punto proyección sobre el eje OX.
Luego, tienes los datos iniciales que necesitas para abordar el problema:
xi = 0, yi = 1 m, vi = v1 = √(5,4) m/s, α = 30°, ax = 0, ay = -g = -9,8 m/s2;
luego, planteas las ecuaciones de posición de Tiro Oblicuo (o Movimiento Parabólico), y queda:
x = xi + vi*cosα*t,
y = yi + vi*senα*t + (1/2)*a*t2,
reemplazas datos, resuelves coeficientes, cancelas el término nulo, y queda:
x ≅ 2,012*t,
y ≅ 1 + 1,162*t - 4,9*t2;
luego, planteas la condición de llegada del cuerpo a nivel del suelo:
x = X,
y = 0,
sustituyes expresiones en los primeros miembros de ambas ecuaciones, y queda:
X ≅ 2,012*t (1),
0 ≅ 1 + 1,162*t - 4,9*t2 (2).
Luego, sumas 4,9*t2 , restas 1,162*t y restas 1 en al ecuación señalada (2), y queda:
4,9*t2 - 1,162*t - 1 ≅ 0,
que es una ecuación polinómica cuadrática, cuyas soluciones son:
a)
t ≅ -0,128 s, que no tiene sentido para este problema,
b)
t ≅ 0,586 s, que es el instante en el cuál el cuerpo alcanza el nivel del suelo;
luego, reemplazas este último valor remarcado en la ecuación señalada (1), resuelves, y queda:
X ≅ 1,179 m.
Espero haberte ayudado.




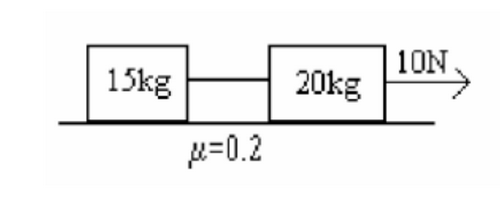 Necesito hallar la tensión de la cuerda y la aceleración, pero no sé cómo empezar.
Necesito hallar la tensión de la cuerda y la aceleración, pero no sé cómo empezar.