-


Antonio Silvio Palmitano
el 22/1/201)
Recuerda que si consideras como puntos fijos a los que corresponden a la fusión del agua y a la ebullición del agua, en condiciones normales de presión y temperatura, entonces tienes que:
- la temperatura de fusión del agua es: 0 °C o 32 ° F,
- la temperatura de ebullición del agua es: 100 °C o 212 °F;
luego, tienes que las diferencias entre las temperaturas de los puntos fijos son: 100 °C y 180 °F, para la escalas Centígrada y Fahrenheit, respectivamente.
Luego, planteas las diferencias entre la temperatura en una misma situación con los puntos fijos inferiores, y queda: (c - 0) y (f - 32);
luego, puedes plantear la proporción:
(f - 32)/(c - 0) = 180/100,
donde tienes la razón entre las diferencias de las expresiones de la temperatura genérica con respecto al punto fijo inferior en el primer miembro, y tienes la razón entre las diferencias de las expresiones entre los puntos fijos en el segundo miembro;
luego, cancelas el término nulo en el denominador del primer miembro, simplificas en el segundo miembro, y queda:
(f - 32)/c = 9/5, multiplicas por 5 y por c en ambos miembros, y queda:
5*(f - 32) = 9*c, aquí divides por 9 en ambos miembros, y luego despejas:
c = 5*(f - 32)/9,
que es la expresión de la temperatura genérica en la escala Centígrada, en funicón de su expresión en la escala Fahrenheit.
Luego, tienes en tu enunciado el valor de la temperatura expresada según la escala Fahrenheit:
f = -185 °F;
luego, reemplazas este valor en la ecuación que tienes remarcada, y queda:
c = 5*(-185 - 32)/9, resuelves el agrupamiento, y queda:
c = 5*(-217)/9, resuelves, y queda:
c ≅ -120,556 °C.
Espero haberte ayudado.


Antonio Silvio Palmitano
el 22/1/202)
Considera la ecuación que tienes remarcada en el ejercicio anterior:
c = 5*(f - 32)/9, multiplicas por 9 y divides por 5 en ambos miembros, y queda:
9*c/5 = f - 32, aquí sumas 32 en ambos miembros, y luego despejas:
f = 9*c/5 + 32 (1),
que es la expresión de la temperatura genérica en la escala Fahrenheit, en función de su expresión en la escala Centígrada.
Luego, tienes el rango de temperaturas en tu enunciado, con las temperaturas expresadas en la escala Centígrada:
110 °C < c < 120 °C,
divides por 5 en los tres miembros de esta inecuación doble (observa que no cambian las desigualdades), y queda:
22 < c/5 < 24,
multiplicas por 9 en los tres miembros de esta inecuación doble (observa que no cambian las desigualdades), y queda:
198 < 9*c/5 < 216,
sumas 32 en los tres miembros de esta inecuación doble, y queda:
230 < 9*c/5 + 32 < 248,
sustituyes la expresión del miembro central según la ecuación señalada (1), y queda:
230 °F < f < 248 °F,
que es el rango de temperaturas de tu enunciado, con las temperaturas expresadas en la escala Fahrenheit.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 21/1/20Puedes designar con L a la longitud del mástil, con lo cuál tienes que el punto de aplicación de las dos tensiones queda expresado: M(0,0,L).
Luego, observa que el vector posición del punto M con respecto al origen de coordenadas queda expresado: p = < 0 ; 0 ; L >.
Luego, planteas la expresión del vector dirección de la fuerza TA, que está aplicada en el punto M y que la cuerda correspondiente está amarrada en el punto D(3,-2,0), y queda:
a = MD = < 3 ; -2 ; -L >, cuyo módulo queda expresado: |a| = √(13 + L2).
Luego, planteas la expresión del vector dirección de la fuerza TB, que está aplicada en el punto M y que la cuerda correspondiente está amarrada en el punto E(-3,2,0), y queda:
b = MD = < -3 ; 2 ; -L >, cuyo módulo queda expresado: |b| = √(13 + L2).
Luego, planteas la expresión vectorial de la fuerza TA, y queda:
TA = |TA|*a/|a|;
luego, planteas la expresión vectorial del momento de esta fuerza con respecto al origen de coordenadas, y queda:
τA = p x TA = p x |TA|*a/|a| = |TA|*(p x a)/|a| (1);
luego, planteas la expresión del producto vectorial del segundo factor de esta expresión, y queda:
p x a = < 0 ; 0 ; L > x < 3 ; -2 ; -L > = < 2*L ; 3*L ; 0 >, sustituyes esta expresión en la expresión del momento de fuerza señalada (1), y queda:
τA = |TA|*< 2*L ; 3*L ; 0 >/|a| (1*).
Luego, planteas la expresión vectorial de la fuerza TB, y queda:
TB = |TB|*b/|b|;
luego, planteas la expresión vectorial del momento de esta fuerza con respecto al origen de coordenadas, y queda:
τB = p x TB = p x |TB|*b/|b| = |Tb|*(p x b)/|b| (2);
luego, planteas la expresión del producto vectorial del segundo factor de esta expresión, y queda:
p x b = < 0 ; 0 ; L > x < -3 ; 2 ; -L > = < -2*L ; -3*L ; 0 >, sustituyes esta expresión en la expresión del momento de fuerza señalada (2), y queda:
τB = |TA|*< -2*L ; -3*L ; 0 >/|b| (2*).
Luego, observa que la recta dirección del peso del mástil es el eje OZ, y como el origen de coordenadas pertenece a esta recta, entonces tienes que el momento de fuerza del peso con respecto al origen de coordenadas es nulo.
Luego, planteas la expresión del momento de fuerza resultante, y queda:
τO = τA + τB,
sustituyes las expresiones señaladas (1*) (2*) en el segundo miembro, y queda:
τO = |TA|*< 2*L ; 3*L ; 0 >/|a| + |TA|*< -2*L ; -3*L ; 0 >/|b|,
sustituyes los valores de los módulos de las fuerzas que tienes en tu enunciado, y queda:
τO = 400*< 2*L ; 3*L ; 0 >/|a| + 700*< -2*L ; -3*L ; 0 >/|b|,
sustituyes las expresiones de los módulos de los vectores direcciones de las fuerzas, y queda:
τO = 400*< 2*L ; 3*L ; 0 >/√(13 + L2) + 700*< -2*L ; -3*L ; 0 >/√(13 + L2),
extraes factor común (100), extraes denominador común [√(13 + L2)], y queda:
τO = 100*( 4*< 2*L ; 3*L ; 0 > + 7*< -2*L ; -3*L ; 0 > )/√(13 + L2),
resuelves la combinación lineal vectorial en el segundo factor, y queda:
τO = 100*( < -6*L ; -9*L ; 0 > )/√(13 + L2),
extraes factor común escalar (-3*L) en el factor vectorial, y queda:
τO = 100*( -3*L*< 2 ; 3 ; 0 > )/√(13 + L2),
resuelves la multiplicación de factores escalares, y queda:
τO = -300*L*< 2 ; 3 ; 0 >/√(13 + L2),
que es la expresión del momento de fuerza resultante con respecto al origen de coordenadas, en función de la longitud del mástil (si es necesario, puedes introducir el factor y también el divisor en las componentes del factor vectorial, y queda:
τO = < -600*L/√(13 + L2) ; -900/√(13 + L2) ; 0 >.
Espero haberte ayudado.
-
Me gustaría asber cómose hace este problema y a qué se correpsonde la fuerza F de la izquierda del sistema.


Antonio Silvio Palmitano
el 20/1/20Vamos con una orientación.
Para el bloque colgante, establece un sistema de referencia con eje OX horizontal con sentido positivo hacia la derecha según tu figura, y con eje OY vertical con sentido positivo hacia abajo; luego, observa que sobre este bloque están aplicadas cinco fuerzas, de las que indicamos sus módulos, direcciones y sentidos:
Peso: Pc = Mc*g, vertical hacia abajo,
Tensión de la cuerda: T, vertical hacia arriba,
Acción normal de la pared de la cuña: Nc, horizontal hacia la izquierda,
Rozamiento dinámico de la pared de la cuña: frdc = μd*Nc, vertical, hacia arriba,
Fuerza externa: F, horizontal hacia la derecha;
luego, aplicas la Segunda Ley de Newton (observa que este bloque se desplaza con dirección vertical con sentido hacia abajo), y quedan las ecuaciones (observa que sustituimos las expresiones de los módulos de las fuerzas):
F - Nc = 0, de aquí despejas: Nc = F (1),
Mc*g - T - μd*Nc = Mc*a,
sustituyes la expresión señalada (1) en la segunda ecuación, y luego despejas: T = Mc*g - μd*F - Mc*a (2).
Para el bloque deslizante, establece un sistema de referencia con eje OX paralelo a la rampa con sentido positivo hacia arriba según tu figura, y con eje OY perpendicular a la rampa con sentido positivo hacia arriba; luego, observa que sobre este bloque están aplicadas cuatro fuerzas, de las que indicamos sus módulos, direcciones y sentidos:
Peso: Pd = Md*g, vertical hacia abajo,
Tensión de la cuerda: T, paralela a la rampa hacia arriba,
Acción normal de la rampa: Nd, perpendicular a la rampa hacia arriba,
Rozamiento dinámico de la rampa: frdd = μd*Nd, paralela a la rampa hacia abajo;
luego, aplicas la Segunda Ley de Newton (observa que este bloque se desplaza con dirección paralela a la rampa con sentido hacia arriba), y quedan las ecuaciones (observa que sustituimos las expresiones de los módulos de las fuerzas):
T - Md*g*senθ - μd*Nd = Md*a,
Nd - Md*g*cosθ = 0, de aquí despejas: Nd = Md*g*cosθ (3),
sustituyes la expresión señalada (3) en la primera ecuación, y luego despejas: T = Md*g*senθ + μd*Md*g*cosθ + Md*a (4).
Luego, en la ecuación señalada (2) despejas:
F = (Mc*g - Mc*a - T)/μd, aquí sustituyes la expresión remarcada y señalada (4), distribuyes el tercer término de su numerador, y queda:
F = (Mc*g - Mc*a - Md*g*senθ - μd*Md*g*cosθ - Md*a)/μd (5).
Luego, queda que reemplaces datos (a = 1 m/s2, Mc = 5 Kg, Md = 5 Kg, μd = 0,2, g = 9,8 m/s2, θ = 30°) en las ecuaciones remarcadas y señaladas (4) (5), y hagas los cálculos.
Espero haberte ayudado.
-
Al aplicar una diferencia de potencial de 300 μV entre los extremos de una barrita de plata de 20 mm de
longitud y 0.5 mm2 de sección circula una corriente de 500 mA. La temperatura de la barrita es de 300 K.
a) Determine la conductividad eléctrica de la muestra
b) Ame el valor de la conductividad térmica de la plata
c) Determine la densidad de corriente en la barrita
d) Determine el número de electrones de conducción por m3 (suponga que cada átomo proporciona un
electrón de conducción (la masa atómica de la plata es 107.87 y la densidad 10.5 g / cm3
)
e) Determine la velocidad térmica de los electrones según los modelos de Drude y de Fermi de electrones
libres
f) Calcular el tiempo que tarda un electrón en recorrer la barrita
-
 Tengo dudas en el siguiente problema:
Tengo dudas en el siguiente problema:Una onda se propaga por una cuerda en el sentido positivo del eje x. La amplitud, la longitud de onda y el periodo valen (0’5m, 1’7m y 2,5s) respectivamente. Además, la fase de la onda vale π/2 (rad/s)
a) Ecuación de la onda
b) Ecuación de oscilación periódica que tiene lugar en x=0,8m
c) Energía cinética máxima del segmento de cuerda localizado en torno al punto P (considera un segmento de cuerda de masa m=10gramos)
No se si lo tengo bien resuelto, si me lo pueden revisar y decirme si tengo algún fallo por favor.


Antonio Silvio Palmitano
el 20/1/20Planteas la expresión de la función elongación (observa que la onda se desplaza con el sentido positivo del eje OX), y queda:
y(t,x) = A*sen(ω*t - k*x + δ) (1).
Planteas la expresión de la función velocidad de oscilación de un punto (observa que la onda se desplaza con el sentido positivo del eje OX, y observa que uno de los datos es la rapidez máxima con la que oscila el agua en la dirección del eje OY), y queda:
vy(t,x) = ω*A*cos(ω*t - k*x + δ) (2).
Luego, tienes los datos de tu enunciado:
A = 0,5 m,
λ = 1,7 m, de donde tienes: k = 2π/λ = 2π/1,7 ≅ 3,696 rad/m;
T = 2,5 s, de donde tienes: f = 1/T = 1/2,5 = 0,4 Hz, y de aquí tienes: ω = 2π*f = 2π*0,4 ≅ 2,513 rad/s;
δ = π/2 rad (observa que aquí debes corregir la unidad de medida que tienes consignada en tu enunciado.
a)
Reemplazas los valores que tienes remarcados en la expresión de la función elongación señalada (1), y queda:
y(t,x) ≅ 0,5*sen(2,513*t - 3,696*x + π/2) m (2).
b)
Tienes el valor de la posición en estudio: x = 0,8 m, reemplazas este valor en la ecuación remarcada y señalada (2), resuelves términos numéricos en el argumento del seno, y queda:
y(t,0,8) ≅ 0,5*sen(2,513*t - 1,626) m.
c)
Planteas la expresión de la rapidez de propagación de la onda, y queda:
v = ω/k, aquí reemplazas valores, y queda: v ≅ 2,513/3,696 ≅ 0,680 m/s;
luego, planteas la expresión de la energía cinética máxima que puede alcanzar un punto genérico de la cuerda (observa que debes considerar solamente su velocidad en la dirección de oscilación, ya que un punto específico de la cuerda no se traslada en la dirección de propagación de la onda), y queda:
ECM = (1/2)*M*vyM2 = (1/2)*M[(ω*A)2 = (1/2)*M*ω2*A2,
evalúas esta expresión para un segmento cuyo punto medio es el punto genérico en estudio, cuyas masa es: M = 10 g = 0,01 Kg, y queda:
ECM ≅ (1/2)*0,01*2,5132*0,52 ≅ 0,008 J.
Espero haberte ayudado.
-


Breaking Vlad
el 20/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)


Antonio Silvio Palmitano
el 20/1/20Observa que el intervalo de tiempo mínimo que emplea el oscilador para desplazarse desde su posición de equilibrio hasta un punto de elongación máxima es igual a la cuarta parte del periodo (observa que para completar una oscilación completa debe, además: regresar a su posición de equilibrio, dirigirse al punto opuesto de máxima elongación, y regresar a su posición de equilibrio), por lo que puedes plantear la ecuación:
(1/4)*T = 3/2 (en segundos),
multiplicas por 4 en ambos miembros, y queda:
T = 6 s,
por lo que puedes concluir que la opción señalada (E) es la respuesta correcta.
Espero haberte ayudado.
-
 Tengo dudas en el siguiente problema:
Tengo dudas en el siguiente problema:Una onda armónica se propaga por el agua en el sentido positivo del eje X con frecuencia 2Hz. Su longitud de onda es de 2m y la velocidad máxima de la superficie del agua en vertical es de 5m/s. Si en el origen de coordenadas y en t=0, la altura del agua es de 0,4m. ¿Cuál es la ecuación de onda y con qué velocidad se propaga?
No sé si lo he resuelto de forma correcta, si me lo pueden revisar y decirme si está bien o no por favor.


Antonio Silvio Palmitano
el 20/1/20Planteas la expresión de la función elongación (observa que la onda se desplaza con el sentido positivo del eje OX), y queda:
y(t,x) = A*sen(ω*t - k*x + δ) (1).
Planteas la expresión de la función velocidad de oscilación de un punto (observa que la onda se desplaza con el sentido positivo del eje OX, y observa que uno de los datos es la rapidez máxima con la que oscila el agua en la dirección del eje OY), y queda:
vy(t,x) = ω*A*cos(ω*t - k*x + δ) (2).
Luego, tienes los datos de tu enunciado:
f = 2 Hz, de donde tienes: ω = 2π*f = 2π*2 = 4π rad/s;
λ = 2 m, de donde tienes: k = 2π/λ = 2π/2 = π rad/m;
vyM = 5 m/s, de donde tienes: ω*A = vyM, aquí despejas, y tienes: A = vyM/ω = 5/(4π) m;
y(0,0) = 0,4 m, aquí sustituyes la expresión señalada (1) evaluada en el primer miembro, cancelas términos nulos, y queda:
A*sen(δ) = 0,4, reemplazas el valor de la amplitud de oscilación que tienes remarcado, y queda:
5/(4π)*sen(δ) = 0,4, multiplicas por 4π y divides por 5 en ambos miembros, y queda:
sen(δ) = 0,32π ≅ 1,005,
que no es un valor válido para la función seno,
por lo que tienes que verificar que los datos de tu enunciado estén bien consignados, o consultar con tus docentes al respecto, porque con los datos que tienes en tu enunciado no es posible determinar al fase inicial (δ) y, por lo tanto, tampoco es posible determinar la expresión de la función elongación.
Luego, planteas la expresión de la rapidez de propagación de la onda, y queda:
v = ω/k = 4π/π = 4 m/s.
Espero haberte ayudado.
-
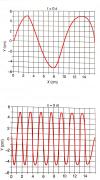
Hola.
¿Cómo es posible que estas dos gráficas representen a una misma onda, cuando a tiempo igual a cero una va hacia arriba y otra hacia abajo?


Antonio Silvio Palmitano
el 19/1/20Observa que tienes la gráfica posición-elongación (x-y) en la imagen superior. para el instante fijo: t = 0, por lo cuál tienes la gráfica de la onda en dicho instante.
Observa que tienes la gráfica tiempo-elongación (t-y) en la imagen inferior, para la posición fija: x = 0, por lo que tienes que la gráfica describe la oscilación del punto cuya abscisa es x = 0.
Recuerda que la función de onda es una función de dos variables: tiempo (t) y posición (x), por lo que tienes que las dos imágenes corresponden a diferentes consideraciones.
Por ejemplo, considera la expresión de la función de onda (aclaramos: no corresponde a las gráficas de las imágenes de tu figura):
y(t,x) = 10*sen(2π*t + 2*x);
luego, si evalúas para el instante fijo: t = 0, reemplazas este valor en el argumento del seno, resuelves, y queda:
y(0,x) = 10*sen(2x);
luego, si evalúas para la posición fija: x = 0, reemplazas este valor en el argumento del seno, resuelves, y queda:
y(t,0) = 10*sen(2π*t).
Espero haberte ayudado.
-
Buenas tardes. Espero puedan ayudarme. Gracias
Una hormiga anda por el suelo con un vector aceleración constante. A las 12 h 03 min 33 s sale
del rincón de una habitación cuadrada de 2 m de lado. A las 12 h 06 min 33 s llega al rincón opuesto.
¿Cuál es su posición a las 12 h 04 min 33 s?


Antonio Silvio Palmitano
el 18/1/20Establece un sistema de referencia con instante inicial: ti = 0 correspondiente a las 12:03:33 horas reloj, con origen de coordenadas en el rincón de partida de la hormiga, con eje OX según una de las aristas del cuadrado, y con el eje OY en la otra arista, y como puedes apreciar si haces un dibujo, tienes que los dos ejes coordenados son perpendiculares.
Luego, planteas las expresiones vectoriales de la posición inicial y de la posición final de la hormiga, y queda:
ri = < 0 ; 0 >, al que corresponde el instante: ti = 0,
rf = < 2 ; 2 > m, al que corresponde el instante: tf = 3 min = 180 s.
Luego, planteas la expresión vectorial de la velocidad inicial de la hormiga, que consideramos parte desde el reposo, y queda:
vi = < 0 ; 0 >.
Luego, planteas la expresión vectorial de la aceleración de la hormiga, y queda:
a = < ax ; ay > m/s2, cuyas componentes debes determinar.
Luego, planteas la ecuación vectorial de posición de Movimiento Rectilíneo Uniformemente Variado, y queda:
r = ri + vi*t + (1/2)*a*t2,
sustituyes la expresión de la posición inicial, la expresión de la velocidad inicial, y la expresión de la aceleración que tienes planteadas, y queda:
r = < 0 ; 0 > + < 0 ; 0 >*t + (1/2)*< ax ; ay >*t2,
cancelas los dos primeros términos nulos en el segundo miembro, y queda:
r = (1/2)*< ax ; ay >*t2,
resuelves los productos en el segundo miembro, y queda:
r = < (1/2)*ax*t2 ; (1/2)*ay*t2 > (1);
luego, sustituyes la expresión de la posición final en el primer miembro de la ecuación señalada (1), reemplazas el valor del instante final en su segundo miembro, resuelves los coeficientes en la expresión vectorial del segundo miembro, y queda:
< 2 ; 2 > = < 16200*ax ; 16200*ay >,
y por igualdad entre expresiones vectoriales, igualas componente a componente, y quedan las ecuaciones:
2 = < 16200*ax, y de aquí despejas: ax = 1/8100 m/s2,
2 = < 16200*ay, y de aquí despejas: ay = 1/8100 m/s2,
reemplazas los valores remarcados en la ecuación vectorial de posición señalada (1), resuelves coeficientes, y queda:
r = < (1/16200)*t2 ; (1/16200)*t2 > (2),
que es la expresión vectorial de la posición de la hormiga que corresponde a la situación planteada en tu enunciado.
Luego, tienes el horario reloj en estudio: 12:04:33, al que corresponde el instante: t = 1 min = 60 s,
reemplazas este último valor remarcado en las componentes de la expresión vectorial remarcada y señalada (2), y queda:
r = < (1/16200)*602 ; (1/16200)*602 >,
resuelves, y queda:
r = < 2/9 ; 2/9 > m ≅ < 0,222 ; 0,222 > m,
que es la posición de la hormiga para el horario en estudio.
Espero haberte ayudado.