-
Paso un problema que he intendado hacer pero no se si esta bien.
Un muchacho se encuentra tranquilamente sentado en el banco de un parque cuando le pasa una muchacha andando a 5,04 km/h. Tras pensarselo 5s, decide salir tras ella con una aceleración de 0'5 m/s2. Que distancia recorrerà hasta alcanzarla?


Antonio Silvio Palmitano
el 11/2/20Establece un sistema de referencia con origen de coordenadas en el banco, con instante inicial: ti = 0 correspondiente al instante en el cuál la muchacha pasa por el banco, y con eje OX horizontal con dirección y sentido positivo acordes al desplazamiento de la muchacha.
Luego, tienes los datos iniciales de la muchacha: ti = 0, xi = 0, v = 5,04 Km/h = 5,04*1000/3600 = 1,4 m/s, planteas la ecuación de posición de Movimiento Rectilíneo Uniforme, cancelas términos nulos, y queda:
x1 = 1,4*t (1).
Luego, tienes los datos iniciales del muchacho: ti = 5 s, xi = 0, vi = 0, a = 0,5 m/s, planteas la ecuación de posición de Movimiento Rectilíneo Uniformemente Acelerado, resuelves coeficientes, cancelas términos nulos, y queda:
x2 = 0,25*(t - 5)2 (2).
Luego, planteas la condición de encuentro (las posiciones de ambos móviles coinciden):
x2 = x1, sustituyes las expesiones señaladas (2) (1), y queda:
0,25*(t - 5)2 = 1,4*t, multiplicas por 4 en ambos miembros, y queda:
1*(t - 5)2 = 5,6*t, desarrollas el primer miembro, y queda:
t2 - 10*t + 25 = 5,6*t, restas 5,6*t en ambos miembros, y queda
t2 - 15,6*t + 25 = 0, multiplicas por 10 en todos los términos, y queda:
10*t2 - 156*t + 250 = 0, que es una ecuación polinómica cuadrática, cuyas soluciones son:
a)
t = (156 - √[14336])/20 ≅ 1,813 s, que no tiene sentido para este problema (observa que el muchacho comenzó su desplazamiento en el instante t = 5 s);
b)
t = (156 + √[14336])/20 ≅ 13,787 s,
reemplazas este último valor en las ecuaciones señaaldas (1) (2), y queda:
x1 ≅ 1,4*13,787 ≅ 19,301 m,
x2 ≅ 0,25*(13,787 - 5)2 ≅ 0,25*8,7872 ≅ 19,301 m,
por lo que puedes concluir que la posición de encuentro es: x ≅ 19,301 m.
Espero haberte ayudado.
-
Me pueden ayudar con ese ejercicio? No sé cómo hacerlo, intenté sacar su volumen pero no tengo el radio ni la altura



Breaking Vlad
el 10/2/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
¿Me puede ayudar alguien con este ejercicio?
5.- En un espectáculo ecuestre, un caballo requiere saltar un obstáculo de 1.5 metros de altura. Si parte de una velocidad inicial de 8m/s en el eje horizontal y 8m/s en el eje vertical; calcule la distancia horizontal recorrida y altura máxima alcanzada por el caballo. A partir de ello indique si fue posible que el caballo saltara el obstáculo o no.


Antonio Silvio Palmitano
el 9/2/20Considera un sistema de referencia con eje OX horizontal con sentido positivo acorde al desplazamiento del caballo, con eje OY vertical con sentido positivo hacia arriba, con origen de coordenadas en la posición dónde el animal comienza su salto, y con instante inicial: ti = 0 correspondiente al inicio del salto.
Luego, tienes los datos:
xi = 0, yi = 0 (componentes de la posición inicial),
vx = 8 m/s, vyi = 8 m/s (componentes de la velocidad inicial),
ax = 0, ay = -g = -9,8 m/s2 (componentes de la aceleración).
Luego, planteas las expresiones de las componentes de la posición y de la velocidad de Tiro Oblicuo (o Movimiento Parabólico), y queda:
x = xi + vx*t (observa que omitimos el término correspondiente a la aceleración, por ser nulo),
y = yi + vxi*t + (1/2)*ay*t2,
Vx = vx (observa que es constante),
Vy = vyi + ay*t;
luego, reemplazas datos, resuelves coeficientes, cancelas términos nulos, y queda:
x = 8*t (1),
y = 8*t - 4,9*t2 (2),
Vx = 8 m/s (3),
Vy = 8 - 9,8*t (4).
a)
Planteas la condición de llegada del caballo a nivel del suelo: y = 0, sustituyes la expresión señalada (2), ordenas términos, y queda la ecuación:
-4,9*t2 + 8*t = 0, que es una ecuación polinómica cuadrática, cuyas soluciones son:
1°)
t = 0, que es el instante de inicio del salto;
2°)
t = 8/4,9 ≅ 1,633 s, que es el instante en el cuál el caballo vuelve a tocar el suelo,
luego, reemplazas este último valor remarcado en la ecuación señalada (1), resuelves, y queda:
xA = 64/4,9 ≅ 13,061 m, que es el valor del desplazamiento horizontal del caballo desde el inicio del salto hasta que llega nuevamente a nivel del suelo.
b)
Planteas la condición de altura máxima ("el caballo no asciende ni desciende"): Vy = 0, sustituyes la expresión señalada (4), y queda la ecuación:
8 - 9,8*t = 0, y de aquí despejas:
t = 8/9,8 ≅ 0,816 s, que es el instante en el cuál el caballo alcanza la altura máxima en su salto,
luego, reemplazas este último valor remarcado en la ecuacion señalada (2), resuelves, y queda:
yM≅ 3,265 m, que es el valor de la máxima altura que obtiene el caballo en su salto.
Luego, puedes concluir que el caballo consigue sobrepasar el obstáculo, y habría que señalar que éste debe ubicarse en el punto medio del desplazamiento horizontal del animal durante su salto.
Espero haberte ayudado.
-
Hola buenas, mi pregunta es sobre cómo hacer el apartado (c) ya que lo he intentado de varias formas pero no llego
a la solución ( 13,07 ) .


Antonio Silvio Palmitano
el 8/2/20c)
Establece un sistema de referencia con eje OY vertical con sentido positivo hacia abajo, y con sentido de giro positivo antihorario.
Luego, observa que sobre la polea están aplicadas dos fuerzas: peso y tensión de la cuerda, por lo que aplicas la Segunda Ley de Newton para traslaciones y para giros (observa que consideramos los momentos de fuerza con respecto al eje de la polea), y quedan las ecuaciones (observa que sustituimos la expresión del módulo del peso, y la expresión del momento de inercia de la polea):
M*g - T = M*a, de aquí despejas: T = M*(g - a) (1),
R*T = (1/2)*M*R2*α, aquí multiplicas por 2 y divides por R en ambos miembros, y queda: 2*T = M*R*α (2).
luego, sustituyes la expresión señalada (1) en la ecuación señalada (2), y queda:
2*M*(g - a) = M*R*α, divides por M en ambos miembros, distribuyes el primer miembro, y queda:
2*g - 2*a = R*α, sustituyes la expresión del módulo de la aceleración lineal de la polea, y queda:
2*g - 2*R*α = R*α, restas R*α y restas 2*g en ambos miembros, y queda:
-3*R*α = -2*g, divides por -3 y por R en ambos miembros, y queda:
α = (2/3)*g/R;
luego, reemplazas datos, y queda:
α = (2/3)*9,8/0,5, resuelves, y queda:
α ≅ 13,0667 rad/s2.
Espero haberte ayudado.
-
como puedo encontrar el tiempo en que tarda una esfera que estaba hundida en ponerse en contacto con la superficie del fluido
la esfera estaba totalmente sumergida en el fluido porque una cuerda la sostenía con el fondo y luego se corta


Antonio Silvio Palmitano
el 8/2/20Vamos con una orientación.
Observa que sobre la esfera están aplicadas (una vez que se ha cortado la soga) dos fuerzas verticales: peso y empuje del líquido, por lo que aplicas la Segunda Ley de Newton, y queda la ecuación (consideramos un sistema de referencia con eje OY vertical con sentido positivo hacia arriba, con origen de coordenadas en el fondo del recipiente, y con instante inicial: ti = 0 correspondiente al instante en el cuál se corta la cuerda):
E - P = Me*a,
sustituyes las expresiones de los módulos de las fuerzas, y queda:
δL*Ve*g - Me*g = Me*a,
sustituyes la expresión de la masa de la esfera, y queda:
δL*Ve*g - δe*Ve*g = δe*Ve*a,
divides por Ve en todos los términos, y queda:
δL*g - δe*g = δe*a,
divides por en todos los términos, extraes factor común (g) en el primer miembro, y luego despejas:
a = (δL/δe - 1)*g,
que es la expresión de la aceleración de las esfera.
Luego, planteas la ecuación de posición de Movimiento Rectilíneo Uniformemente Acelerado para el punto "más alto" de la esfera (observa que consideramos que la esfera es homogénea y que parte desde el reposo, y que la posición inicial del punto de la esfera en estudio es 2*R), y queda:
y = 2*R + (1/2)*a*t2,
sustituyes la expresión de la aceleración, y queda:
y = 2*R + (1/2)*(δL/δe - 1)*g*t2 (1).
Luego, observa que la posición final del punto más alto de la esfera es H (valor de la profundidad del recipiente), por lo que sustituyes esta última expresión en la ecuación señalada (1), y queda:
H = 2*R + (1/2)*(δL/δe - 1)*g*t2,
restas 2*R en ambos miembros, y queda:
H - 2*R = (1/2)*(δL/δe - 1)*g*t2,
multiplicas por 2 y divides por (δL/δe - 1)*g en ambos miembros, y luego despejas:
t2 = 2*(H - 2*R)/[(δL/δe - 1)*g],
extraes raíz cuadrada positiva en ambos miembros, y queda:
t = √(2*(H - 2*R)/[(δL/δe - 1)*g]),
que es la expresión del instante en el cuál el punto "más alto" de la esfera alcanza el nivel de la superficie del líquido, en función de la profundidad del recipiente, del radio de la esfera, de la densidad de masa del líquido, de la densidad de masa de la esfera, y del módulo de la aceleración gravitatoria terrestre.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 7/2/203)
Establece un sistema de referencia con origen de coordenadas en el punto O, con eje OX horizontal con sentido positivo hacia el punto A, y con eje OY vertical con sentido positivo hacia arriba.
Luego, como tienes que las dos barras son homogéneas, observa entonces que sus centros de masas se encuentran en sus centros geométricos, en este caso puntos medios:
xmOA = 0,5/2 = 0,25 m, ymOA = 0 (coordenadas del punto medio de la barra OA),
xmCB = 0,5 m, ymCB = 0 (coordenadas del punto medio de la barra CB).
Luego, planteas las expresiones de las coordenadas del centro de masas del conjunto formado por las dos barras (observa que consideramos que las masas de las barras están concentradas en sus puntos medios), y queda:
xc = (MOA*xmOA + MCB*xmCB)/(MOA + MCB),
yc = (MOA*ymOA + MCB*ymCB)/(MOA + MCB),
reemplazas los valores de las masas de las barras y los valores de las coordenadas de sus puntos medios, y queda:
xc = (8*0,25 + 8*0,5)/(8 +8) = (2 + 4)/16 = 3/8 = 0,375 m,
xc = (8*0 + 8*0)/(8 +8) = (0 + 0)/16 = 0,
por lo que tienes que el centro de masas del conjunto formado por las dos barras se encuentra en el punto:
C(0,375;0) m.
Espero haberte ayudado.


Antonio Silvio Palmitano
el 7/2/206)
Establece un sistema de referencia con eje OX sobre el eje de simetría de la barra con sentido positivo hacia la derecha según tu figura, con eje OY vertical con sentido positivo hacia arriba, y con origen de coordenadas en la unión de los dos trozos de la barra, y observa que empleamos unidades internacionales.
Luego, planteas las expresiones de las coordenadas del punto medio del trozo izquierdo, y queda:
xmi = -0,40/2 = -0,2 m, ymi = 0;
luego, planteas la expresión de la masa del trozo izquierdo, y queda:
Mi = δPb*Vi = δPbr*δa*π*r2*L.
Luego, planteas las expresiones de las coordenadas del punto medio del trozo derecho, y queda:
xmd = 0,40/2 = 0,2 m, ymd = 0;
luego, planteas la expresión de la masa del trozo derecho, y queda:
Md = δCu*Vd = δCur*δa*π*r2*L.
Luego, planteas la expresión de la abscisa del centro de masas de la barra compuesta, y queda:
xc = (Mi*xmi + Md*xmd)/(Mi + Md),
sustituyes las expresiones de las masas de los trozos, y queda:
xc = (δPbr*δa*π*r2*L*xmi + δCur*δa*π*r2*L*xmd)/(δPbr*δa*π*r2*L + δCur*δa*π*r2*L),
extraes factores comunes (δa*π*r2*L) en el numerador y en el denominador, simplificas, y queda:
xc = (δPbr*xmi + δCur*xmd)/(δPbr + δCur),
reemplazas valores, y queda:
xc = (11,37*[-0,2] + 8,91*0,2)/(11,37 + 8,91) = 0,2*(-11,37 + 8,91)/20,28 = 0,2*(-2,46)/20,28 ≅ -0,024 m.
Luego, planteas la expresión de la ordenada del centro de masas de la barra compuesta, y queda:
yc = (Mi*ymi + Md*ymd)/(Mi + Md),
sustituyes las expresiones de las ordenadas de los puntos medios de los trozos, y queda:
yc = (Mi*0 + Md*0)/(Mi + Md),
resuelves el numerador, y queda:
yc = 0/(Mi + Md),
resuelves, y queda:
yc = 0.
Luego, puedes concluir que el centro de masas de la barra compuesta se encuentra, aproximadamente, en el punto:
C(-0,024;0) m.
Luego, planteas la expresión del extremo izquierdo de la barra compuesta, y queda: M(-0,4;0) m;
luego, planteas la expresión de la distancia entre este punto y el centro de masas, y queda:
d(MC) = xC - xM, reemplazas valores, y queda:
d(MC) ≅ -0,024 - (-0,4), resuelves, y queda:
d(MC) ≅ 0,376 m ≅ 37,6 cm.
Espero haberte ayudado.
-
Buenas tardes, alguien me puede ayudar con este problema? Muchas gracias


Antonio Silvio Palmitano
el 6/2/20Vamos con una orientación.
Si tienes que las resistencias señaladas R3 y R4 están conectadas a tierra (V = 0), entonces puedes plantear las ecuaciones:
I1 = I2 + I3 (correspondiente al primer nudo),
(R1 + R2)*I1 + R3*I2 = V (correspondiente a la trayectoria abierta más corta),
(R1 + R2)*I1 + R4*I3 = V (correspondiente a la trayectoria abierta más larga).
Luego, queda que reemplaces los valores de las resistencias y del potencial, y resuelvas el sistema de ecuaciones.
Espero haberte ayudado.
-
hola alguien me puede ayudar con este ejercicio por favor
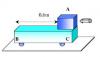 Se dispara horizontalmente una bala de 30 g con una rapidez de 500m/s que se incrusta en un bloque A de 5kg. el coeficiente de rozamiento dinamico entre el bloque A y el carreton BC es de 0.50. debido al rozamiento el bloque A recorre cierta distancia sobre el carreton hasta detenerse. sabiendo que la masa del carreton es de 4kg y que puede rodar libremente a) velocidad del bloque A justo luego del impacto b)aceleracion que adquiere el carreton luego del impacto c)la distancia que recorre el bloque A sobre el carreton d)la velocidad final del conjunto carreton bloque luego de que el bloque A se detiene e) perdida de energia en todo el proceso
Se dispara horizontalmente una bala de 30 g con una rapidez de 500m/s que se incrusta en un bloque A de 5kg. el coeficiente de rozamiento dinamico entre el bloque A y el carreton BC es de 0.50. debido al rozamiento el bloque A recorre cierta distancia sobre el carreton hasta detenerse. sabiendo que la masa del carreton es de 4kg y que puede rodar libremente a) velocidad del bloque A justo luego del impacto b)aceleracion que adquiere el carreton luego del impacto c)la distancia que recorre el bloque A sobre el carreton d)la velocidad final del conjunto carreton bloque luego de que el bloque A se detiene e) perdida de energia en todo el proceso


Antonio Silvio Palmitano
el 6/2/20Establece un sistema de referencia en reposo con respecto al suelo, con eje OX con dirección y sentido positivo acordes al desplazamiento de la bala entes del impacto, con eje OY vertical con sentido positivo hacia arriba, y con origen de coordenadas en la posición inicial del bloque y del carretón (observa que empleamos unidades internacionales, y que consideramos que el valor del módulo de la aceleración gravitatoria terrestre es g = 9,8 m/s2).
a)
Planteas las expresiones de la cantidad de movimiento y de la energía mecánica del sistema bala-bloque-carretón antes del impacto, y queda:
pa = Mb*vb = 0,03*500 = 15 Kg*m/s (1),
EMa = (1/2)*Mb*vb2 = (1/2)*0,03*5002 = 3750 J (2).
Planteas la expresión de la cantidad de movimiento del conjunto bala-bloque inmediatamente después del choque (observa que consideramos que el impacto es instantáneo, y que el conjunto bala-bloque no se ha desplazado sobre el carretón durante el impacto), y queda:
pd = (Mb + MA)*vd = (0,03 + 5)*vd = 5,03*vd (3) (en Kg*m/s) (3).
Luego, planteas conservación de la cantidad de movimiento, y queda la ecuación:
pd = pa, sustituyes las expresiones señaladas (3) (1), y luego despejas:
vd = 15/5,03 ≅ 2,982 m/s,
que es la velocidad del conjunto bala-bloque con respecto al suelo, inmediatamente después del impacto.
b)
Observa que sobre el conjunto bala-bloque están aplicadas tres fuerzas: peso, acción normal del carretón, y rozamiento dinámico del carretón, por lo que aplicas la Segunda Ley de Newton, y quedan las ecuaciones (observa que sustituimos las expresiones de los módulos de las fuerzas):
-μd*Nc = (Mb + MA)*abA,
Nc - (Mb + MA)*g = 0, de aquí despejas: Nc = (Mb + MA)*g = (0,03 + 5)*9,8 = 49,294 N;
luego, reemplazas este valor y los demás datos en la ecuación señalada (1), y luego despejas:
abA = -0,5*49,294/(0,03 + 5) = -4,9 m/s2,
que es la aceleración del conjunto bala-bloque con respecto al suelo.
Observa que sobre el carretón están aplicadas cuatro fuerzas: peso, acción normal resultante del suelo, reacción normal del conjunto bala-bloque, y reacción al rozamiento del conjunto bala-bloque, por lo que aplicas la Segunda Ley de Newton, y quedan las ecuaciones (observa que sustituimos las expresiones de los módulos de las fuerzas):
μd*Nc = Mc*ac,
Ns - Nc - Mc*g = 0,
resuelves este sistema, y queda:
Ns = Nc + Mc*g = 49,294 + 4*9,8 = 88,494 N,
ac = μd*Nc/Mc = 0,5*49,294/4 ≅ 6,162 m/s2,
que es la aceleración del carretón con respecto al suelo.
c)
Planteas las ecuaciones de velocidad de Movimiento Rectilíneo Uniformemente Variado para el conjunto bala-bloque y para el carretón (observa que este último parte desde el reposo inmediatamente después del choque), y queda:
VbA = vd + abA*t,
Vc = ac*t;
luego, observa que cuando el conjunto bala-bloque se detiene con respecto al carretón tienes que su velocidad con respecto al suelo es igual a la velocidad del carretón con respecto al suelo, por lo que igualas expresiones, y queda la ecuación:
ac*t = vd + abA*t, de aquí despejas:
t = vd/(ac - abA), reemplazas valores, y queda:
t ≅ 2,982/(6,162 - [-4,9]) ≅ 0,270 s,
que es el instante en el cuál el conjunto bala-bloque se detiene con respecto al carretón;
luego, reemplazas este último valor y los demás datos en las ecuaciones de velocidad, y queda:
VbA ≅ 2,982 + [-4,9]*0,270 ≅ 1,660 m/s,
Vc ≅ 6,162*0,270 ≅ 1,660 m/s,
por lo que puedes concluir que: vf ≅ 1,660 m/s es la velocidad del conjunto bala-bloque-carretón cuando el conjunto bala-bloque no se desplaza con respecto al carretón.
Luego, planteas las ecuaciones de posición de Movimiento Rectilíneo Uniformemente Variado para el conjunto bala-bloque y para el carretón, y queda:
XbA = vd*t + (1/2)*abA*t2,
Xc = (1/2)*ac*t2,
reemplazas valores, y queda:
XbA ≅ 2,982*0,270 + (1/2)*(-4,9)*0,2702 ≅ 0,627 m,
que es la posición del conjunto bala-bloque cuando se detiene con respecto al carretón, respectiva al suelo,
Xc ≅ (1/2)*6,162*0,2702 ≅ 0,225 m,
que es la posición del carretón cuando el conjunto bala-bloque se detiene con respecto a él, respectiva al suelo.
Luego, planteas la expresión del desplazamiento del conjunto bala-bloque con respecto al carretón, y queda:
ΔXr = XbA - Xc, reemplazas valores, y queda:
ΔXr ≅ 0,627 - 0,225 ≅ 0,402 m.
d)
Planteas la expresión de la energía mecánica final del sistema bala-bloque-carretón, y queda:
EMf = (1/2)*(Mb + MA + Mc)*vf2, reemplazas valores, y queda:
EMf ≅ (1/2)*(0,03 + 5 + 4)*1,6602 ≅ 12,442 J (4).
Luego, planteas la expresión de la variación de energía mecánica durante todo el proceso, y queda:
ΔEM = EMf - EMa, reemplazas los valores señalados (4) (2), y queda:
ΔEM ≅ 12,442 - 3750, resuelves, y queda:
ΔEM ≅ -3737,558 J,
cuyo signo negativo indica que la energía mecánica del sistema ha disminuido a causa de la acción mutua entre la bala y el bloque durante el impacto, y debido además al trabajo de la fuerza de rozamiento dinámico que se ejercieron mutuamente el conjunto bala-bloque y el carretón, mientras hubo desplazamiento relativo entre ellos.
Espero haberte ayudado.














