-
Hola, tengo un nivel de física de 3 Eso y me gustaría ampliar mis conocimientos de física. Me interesa sobre todo la parte relacionada con la mecánica cuántica y física moderna. ¿Que material me recomendais utilizar? ¿Puedo con mi edad abordar esos temas?
Pd: En física del Colegio lo saco todo 10
-
hola, tengo una pregunta.
1.) en la formula de Energia potencial = m*g*h ( siendo las unidades kg,m/s2,m respectivamente ) la unidad con la que se mide la energia potencia = w, pero no entiendo de donde sale w ya que al hacer ese producto las unidades se quedan como kg*m2/s2 , no se va metros con metros ya que ambos multiplican..¿pero como llego al watts final ?
¿ kg*m/s2*m = a kilojulio o a julios ?
gracias por la respuesta que me puedan dar. Saludos.

Antonio Silvio Palmitano
el 19/8/19La Unidad Internacional de Trabajo y Energía es el Joule, que siguiendo la expresión de la energía potencial gravitatoria queda:
[E] = [M]*[g]*[h] = Kg * m/s2 * m = N*m = J (Joule).
Luego, recuerda la expresión de la Potencia en función de la variación de energía, y la unidad internacional correspondiente queda:
[Pot] = [E]/[t] = N*m/s = J/s = W (Watt).
Luego, tienes que la expresión de la unidad de potencia en función de la unidad de Energía y de la unidad de tiempo queda:
W = J/s.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 19/8/19Establece un sistema de referencia usual para Tiro Oblicuo (o Parabólico), con origen de coordenadas en el punto de disparo, con instante inicial: ti = 0 correspondiente al disparo del proyectil..
Luego, tienes los datos:
v0 = 76 m/s (rapidez inicial del proyectil),
α = 34° (ángulo de disparo, con respecto al semieje OX positivo),
g = 9,8 m/s2 (módulo de la aceleración gravitatoria terrestre),
x0 = 0, y0 = 0 (componentes de la posición inicial del proyectil).
Luego, planteas las ecuaciones tiempo-posición, planteas las ecuaciones tiempo-velocidad, cancelas términos nulo, y queda:
x = v0*cosα*t (1),
y = v0*senα*t - (1/2)*g*t2 (2),
vx = v0*cosα (3),
vy = v0*senα - g*t (4).
Luego, planteas la condición de altura máxima, y queda:
vy = 0, sustituyes la expresión señalada (4), y queda:
v0*senα - g*t = 0, y de aquí despejas:
tyM = v0*senα/g (5), que es la expresión del instante en el cuál el proyectil alcanza el punto de altura máxima.
Luego, planteas la expresión del instante en estudio que tienes en tu enunciado, y queda:
te = tyM/2, sustituyes la expresión señalada (5) en el segundo miembro, resuelves, y queda:
te = v0*senα/(2*g) (6).
Luego, sustituyes la expresión señalada (6) en la ecuación señalada (1), y queda:
xe = v0*cosα*( v0*senα/(2*g) ), resuelves, y queda:
xe = v02*cosα*senα/(2*g),
y si aplicas la identidad trigonométrica del seno del doble de un ángulo (sen(2*α) = 2*senα*cosα), entonces queda:
xe = v02*sen(2*α)/(4*g),
que es una expresión de la coordenada horizontal correspondiente al instante en estudio, por lo que solo queda que reemplaces datos en cualquiera de las dos expresiones remarcadas, y luego hagas el cálculo.
Espero haberte ayudado.
-
No los entiendo muy bien ya q mi profe nos dio la clase de apuros aver si me ayudan pld tengo q hacer prueba de esto eb 6 horas


Antonio Silvio Palmitano
el 19/8/1910)
Observa que tienes una palanca de primer género, en la que están aplicadas dos fuerzas que consideramos perpendiculares a la barra, de las que indicamos sus módulos y brazos de momento:
Peso del adulto: Pa = Ma*g, da = 1m,
Peso del niño: Pn = Mn*g, dn = 3m;
luego, planteas la condición de equilibrio, y queda:
Pa*da = Pn*dn, sustituyes las expresiones de los módulos de las fuerzas aplicadas, y queda:
Ma*g*da = Mn*g*dn, divides por g y por da en ambos miembros, y queda:
Ma = Mn*dn/da,
y solo queda que reemplaces los valores de los brazos de momento y de la masa del niño que tienes en tu enunciado, para luego hacer el cálculo (te dejo la tarea).
Espero haberte ayudado.


Antonio Silvio Palmitano
el 19/8/199)
Observa que sobre la barra están aplicadas cuatro fuerzas verticales, de las que indicamos sus módulos, sentidos y brazos de momento con respecto a su eje de giros, que es perpendicular al plano de la figura de tu enunciado, e indicamos además el sentido de giro que producirían:
P1 = M1*g, hacia abajo, d1 = 0,70 m, antihorario;
P2 = M2*g, hacia abajo, d2 = 0,40 m, anti horario;
N, hacia arriba, dN = 0, no produce giro (acción normal del apoyo);
P3 = M3*g, hacia abajo, d3 = 0,30 m, horario.
Luego, aplicas la Primera Ley de Newton, por lo que planteas la condición de equilibrio para traslaciones, planteas la condición de equilibrio para rotaciones (consideramos un eje de posiciones OY vertical con sentido positivo hacia arriba, y consideramos positivo al sentido de giro antihorario), y queda:
N - P1 - P2 - P3 = 0, y de aquí despejas: N = P1 + P2 + P3 (1),
d1*P1 + d2*P2 + dN*N - d3*P3 = 0, cancelas el tercer término (observa que es nulo, y queda:
d1*P1 + d2*P2 - d3*P3 = 0, sustituyes las expresiones de los módulos de las fuerzas, y queda:
d1*M1*g + d2*M2*g - d3*M3*g = 0, divides por g en todos los términos, y queda:
d1*M1 + d2*M2 - d3*M3 = 0, y de aquí despejas:
M3 = (d1*M1 + d2*M2)/d3,
y solo queda que reemplaces valores y hagas el cálculo.
Espero haberte ayudado.
-
Alguien me podría ayudar con este problema? Me confunde la parte en la que la si corta la cuerda horizontal. Ademas creo me falta algún dato? Gracias de antemano.



Antonio Silvio Palmitano
el 20/8/19Establece un sistema de referencia con origen de coordenadas en la esfera, con eje OX perpendicular a la cuerda inclinada con sentido positivo hacia la derecha (y hacia abajo), y con eje OY paralelo a la cuerda inclinada con sentido positivo hacia arriba (y hacia la derecha).
Luego, planteas la Primera Ley de Newton para la situación inicial, y tienes el sistema de ecuaciones:
P*sen(30°) - Th*cos(30°) = 0,
Ti - P*cos(30°) - Th*sen(30°) = 0,
resuelves el sistema, y queda:
Th = P*tan(30°)
Ti1 = P/cos(30°) (1).
Luego, planteas la Segunda Ley de Newton para la situación final, y tiens el sistema de ecuaciones
P*sen(30°) = M*a,
Ti2 - P*cos(30°) = 0,
resuelves el sistema, y queda:
a = g*sen(30°),
Ti2 = P*cos(30°) (2).
Luego, planteas la razón del módulo de la tensión de la cuerda inclinada en la situación final, entre el módulo de la tensión de la cuerda inclinada en la situación inicial, y queda:
Ti2/Ti1 = P*cos(30°) / ( P/cos(30°) ), simplificas, resuelves, y queda:
Ti2/Ti1 = cos2(30°), resuelves, y queda:
Ti2/Ti1 = 3/4,
por lo que tienes que la opción señalada (a) es la respuesta correcta.
Espero haberte ayudado.
-
buenas tardes.
tengo ahora mismo una duda con respecto a cuando los kilogramos los tengo que multiplicar o no *9,8m/segundos cuadrado.
estaba resolviendo el problema que les adjunto en captura. La masa del objeto es de 8kg y al leerlo he pensado que para transformarlos a kilopondios tenia que *9,8m/2 , y al comprobar mi problema con el de un compañero , he visto que no tengo que multiplicar por nada, que la equivalencia es 1kp=1kg ------> 8kg =8Kp.
entonces :
A-¿la masa de un objeto se multiplica *9,8m/s2 , CUANDO? ¿ para que tipo de problemas? ¿solo cuando quiero pasar kilogramos a Newton ? siempre que vea un dato expresado en Kp y otro dato expresado en Kp , someto a esa igualdad de 1Kg=1Kp?
ahora mismo es que tengo bastante confusión con las unidades y las equivalencias...espero su ayuda.
les adjunto el problema original y mi planteamiento que he comprobado que es erroeno. gracias.


Francisco Javier
el 18/8/19Es muy común estar confundido con estos enunciados poco precisos que dan ciertos problemas.
Si te fijas, te mencionan que sobre el alambre se cuelga un peso de 8 kg.
Como ya sabrás, el peso es un tipo de fuerza. Por otro lado, los kilogramos (kg) son una unidad de masa.
Entonces acá viene la confunsión del estudiante; no sabe si el enunciado le esta dando la masa o la fuerza (peso) del objeto.
En estos casos recomiendo leer bien los enunciados. Te dicen que se cuelga un "peso". Osea que los 8 kg tienen que ser una fuerza.
Cuando te dan un peso expresado en kilogramos, lo que te están dando son en realidad los kilogramos-fuerza (kgf).
Esta unidad es equivalente a los kilopondios (kp). Osea: 1 kgf = 1 kp
Una vez aclarado esto, podemos proseguir con el problema.
a)
Debemos determinar la resistencia a la tracción (σ) del alambre. Recordemos que:
σ = F/A
Donde "F" es la fuerza del alambre y "A" el área o sección del alambre.
La fuerza del alambre es igual al peso del objeto colgado debido a que hay equilibrio:
F = w = 8 kgf = 8 kp
El area del alambre lo determinamos aplicando la ecuación pertinente (sección circular):
A = π*r2
Recordando que:
r = d/2 = 2/2 = 1 mm
Entonces:
A = π*(1)2 = π mm2
Aplicando ahora la ecuación de la resistencia a la tracción:
σalambre = F/A = 8/π = 2.5465 kp/mm2
Del enunciado tenemos que:
σ = 20 kp/mm2
Esta claro mas que claro que:
20 kp/mm2 > 2.5465 kp/mm2 → σ > σalambre
Por lo que el alambre no se romperá después que se cuelga el objeto.
b)
Aplicamos la ecuación para el modulo de elasticidad (E):
E = σ/(ΔL/Li)
Donde "ΔL" es la diferencia de la longitud final e inicial de la cuerda y "Li" es la longitud inicial de la cuerda.
Despejando para "ΔL" la ecuación anterior:
ΔL = (σ*Li)/E
Pasamos la longitud inicial a milímetros para hacer concordar unidades.
Recuerda que:
1 m = 1000 mm
Entonces:
Li = 1.5 m*(1000 mm/1 m) = 1500 mm
Reemplazando y desarrollando damos con concluido el problema:
ΔL = (2.5465*1500)/12x103 = 0.3183 mm → ΔL = 0.3183 mm
-
Hola a tod@s.
Tengo problemas para llegar a la expresión que me pide el problema.
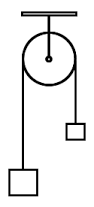
Una pequeña piedra de masa "m" descansa sobre el bloque de masa "m2" de una maquina de Atwood. Determinar la fuerza ejercida por la piedra sobre el bloque "m2"
La solucion es F=(m^2+m1^2+m2^2 / m+m1+m2)*g
Gracias por vuestra ayuda.


Antonio Silvio Palmitano
el 18/8/19A ver si te ayudo con este desarrollo.
Por lo que parece, deberás consultar con tus docentes por la solución que consignan en tu enunciado.
Consideramos que la masa del bloque de la izquierda es M1, que la masa del bloque de la derecha es M2, y que M1 es bastante mayor que M2, por lo que tenemos que la polea gira con sentido antihorario y, por lo tanto, el pequeño bloque de masa M está apoyado sobre el bloque de la derecha según tu imagen.
Luego, observa que sobre el bloque de la izquierda están aplicadas dos fuerzas verticales (su peso y la tensión de la cuerda), considera un sistema de referencia con eje de posiciones OY vertical con sentido positivo hacia abajo; luego, aplicas la Segunda Ley de Newton, y tienes la ecuación:
M1*g - T = M1*a, y de aquí despejas:
T = M1*g - M1*a (1).
Luego, observa que sobre el bloque de la derecha están aplicadas tres fuerzas verticales (su peso, la tensión de la cuerda, y la acción normal que sobre él ejerce el bloque que está apoyado sobre él cuyo sentido es hacia abajo); luego, considera un sistema de referencia con eje de posiciones OY vertical con sentido positivo hacia arriba; luego, aplicas la Segunda Ley de Newton, y tienes la ecuación:
T - M2*g - F = M2*a (2).
Luego, observa que sobre el bloque cuya masa es M están aplicadas dos fuerzas verticales (su peso y la reacción normal que sobre él ejerce el bloque cuya masa es M2; luego, considera un sistema de referencia con eje de posiciones OY vertical con sentido positivo hacia arriba; luego, aplicas la Segunda Ley de Newton, y tienes la ecuación:
F - M*g = M*a, y de aquí despejas:
a = (F - M*g)/M (3).
Luego, sustituyes la expresión señalada (1) en la ecuación señalada (2), y queda:
M1*g - M1*a - M2*g - F = M2*a, y de aquí despejas:
a = (M1*g - M2*g - F)/(M1 + M2) (4).
Luego, igualas las expresiones señaladas (3) (4), y queda:
(F - M*g)/M = (M1*g - M2*g - F)/(M1 + M2), multiplicas por M y por (M1 + M2) en ambos miembros, y queda:
(M1 + M2)*(F - M*g) = M*(M1*g - M2*g - F), distribuyes los factores comunes en ambos miembros, y queda:
(M1 + M2)*F - M*(M1 + M2)*g = M*M1*g - M*M2*g - M*F, sumas M*F y sumas M*(M1 + M2)*g en ambos miembros, y queda:
(M1 + M2)*F + M*F = M*M1*g - M*M2*g + M*(M1 + M2)*g,
extraes factor común (F) en el primer miembro, extraes factor común (M*g) en el segundo miembro, y queda:
(M1 + M2 + M)*F = M*(M1 - M2 + M1 + M2)*g,
cancelas términos opuestos en el agrupamiento del segundo miembro, reduces términos semejantes, y queda:
(M1 + M2 + M)*F = M*(2*M1)*g, divides por (M1 + M2 + M) en ambos miembros, y queda:
F = ( 2*M*M1/(M1 + M2 + M) )*g.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 16/8/19Establece un nivel de referencia en la superficie de separación entre la columna de mercurio y el aire en el tubo de la izquierda, y un eje de posicione (alturas) OY vertical con sentido positivo hacia arriba con origen de coordenadas en el nivel de referencia.
Luego, planteas la expresión de la presión en el tubo de la izquierda en el nivel de referencia, y queda:
pi = patm = 101300 Pa.
Luego, planteas la expresión de la presión en el tubo de la derecha en el nivel de referencia (observa que designamos HHg a la altura de la columna de mercurio con respecto a este nivel), y queda:
pd = ptanque + δHg*g*HHg = 81312,6 + 13600*9,8*HHg = 81312,6 + 133280*HHg.
Luego, planteas la condición de equilibrio para el nivel de referencia, y queda:
81312,6 + 133280*HHg = 101300, restas 81312,6 en ambos miembros, y queda:
133280*HHg = 19987,4, divides por 133280 en ambos miembros, y queda:
HHg ≅ 0,150 m ≅ 15 cm.
Espero haberte ayudado.
-
hola, mando un problema sobre Cuerpos deformables, con el siguiente enunciado que adjunto , y mi pregunta.
¿ como interpretais el dato de que se estira un 3% de su longitud? yo en un principio lo interpreté como que equivalia a Incremento de L, por esa razón estaba atrancada con el problema una vez que calculé el valor de esfuerzo, queriendo seguir con la resolución veo que no podía usar más datos en cualquier otra formula para poder hallar el modulo de Young,entonces miro como ha resuelto un compañero el problema. y veo que para él, ese 3%=0,o3 es el valor de la Desformación y no entiendo porque no es Incremento de L ...¿ no se puede interpretar como que el 3% es lo que ha incrementado ? ¿ si fuese ese dato del 3%Incremento de L, necesitaría mas datos para poder seguir resolviendo por la formula de : Desformación = Incremento de L / longitud. porque calculando el valor de Desfomración ya iria a la formula del Modulo de Young = Esfuerzo/desformación , Gracias por la ayuda que me puedan dar.

Antonio Silvio Palmitano
el 15/8/19Recuerda que los porcentajes, al igual que las fracciones, se expresan con respecto a algo, en este caso a la longitud inicial de la fibra (L).
Luego, tienes que el incremento de la longitud es el 3 % de dicha longitud, por lo tanto queda expresado:
ΔL = 0,03*L, de donde tienes:
ΔL/L = 0,03 = 3*10-2.
Luego, tienes el valor del radio de la sección transversal de la fibra:
R = 0,1 mm = 10-4 m,
y con este valor, tienes que la expresión del área de la sección transversal de la fibra queda expresada:
A = π*R2 = π*(10-4)2 = π*10-8 m2.
Luego, tienes el valor del módulo de la fuerza de tracción aplicada:
F = 10-3 N,
y con este valor planteas la expresión del módulo del esfuerzo normal, y queda:
S = F/A = 10-3/(π*10-8) = 105/π N/m2.
Luego, planteas la expresión del módulo de Young, y queda:
E = S/(ΔL/L) = (105/π) / (3*10-2) = 107/(3*π) N/m2 ≅ 1,061*106 N/m2 ≅ 1,1*106 N/m2.
Espero haberte ayudado.


intento aprender
el 7/9/19hola Antonio Silvio, estaba repasando este problema, y no entiendo este paso que me explicaste:
ΔL = 0,03*L, de donde tienes:
ΔL/L = 0,03 = 3*10-2.
cuando dices : "Luego, tienes que el incremento de la longitud es el 3 % de dicha longitud" ¿ a que Longitud nos referimos sino la tengo ?
y otra duda que se me presenta es: en este tipo de problemas cuando un dato es : Lf o Lo o ΔL ? con esto me sigo confundiendo a veces.... hay algun "truco" para saber que dato corresponde a que ?
muchas, muchas gracias . -
Me podrían ayudar con este problema de mrua porfa???
Dos cuerpos A y B situados a 2km de distancia salen simultáneamente unk en persecución del otro con movimiento acelerado ambos,siendo la aceleración del más lento,el B de 32cm/s². Deben encontrarse a 3025km de distancia del punto de partida del B. Calcula:
A) tiempo que tardan en encontrarse
B)aceleración de A
C) velocidades en el momento de encuentro.


Antonio Silvio Palmitano
el 14/8/19Establece un sistema de referencia con origen de coordenadas en el punto de partida del móvil "más acelerado", con dirección y sentido positivo hacia la posición del móvil "menos acelerado", y con instante inicial: ti = 0 correspondiente al instante de partida de ambos móviles.
Luego, tienes los datos correspondientes al móvil A (el "más acelerado"):
xi = 0 (posición inicial),
vi = 0 (velocidad inicial),
aA = a determinar (aceleración);
luego, planteas las ecuaciones tiempo-posición (x = xi + vi*t + (1/2)*a*t2) y tiempo-velocidad (v = vi + a*t) de Movimiento Rectilíneo Uniformemente Variado, reemplazas datos, cancelas términos nulos, y queda:
xA = (1/2)*aA*t2 (1),
vA = aA*t (2).
Luego, tienes los datos correspondientes al móvil B (el "menos acelerado"):
xi = 2 Km = 2000 m (posición inicial),
vi = 0 (velocidad inicial),
aB = 32 cm/s2 = 0,32 m/s2 (aceleración);
luego, planteas las ecuaciones tiempo-posición (x = xi + vi*t + (1/2)*a*t2) y tiempo-velocidad (v = vi + a*t) de Movimiento Rectilíneo Uniformemente Variado, reemplazas datos, resuelves coeficientes, cancelas términos nulos, y queda:
xB = 2000 + 0,16*t2 (3),
vB = 0,32*t (4).
a)
Tienes los datos para establecer la posición de encuentro (observa que los móviles se encuentran a 3025 m del punto de partida del móvil B, y observa que consideramos que esta distancia está expresada en metros):
xe = 2000 + 3025 = 5025 m;
luego, remplazas este valor en la ecuación señalada (3), y queda:
5025 = 2000 + 0,16*t2, restas 2000 en ambos miembros, y queda:
3025 = 0,16*t2, divides en ambos miembros por 0,16, y queda:
18906,25 = t2, extraes raíz cuadrada positiva en ambos miembros, y luego despejas:
t = √(18906,25) s = 137,5 s,
que es el valor del instante de encuentro de ambos móviles.
b)
Reemplazas los valores de las coordenadas de encuentro (xe = 5025 m y t = 137,5 s) en la ecuación señalada (1), y queda:
5025 = (1/2)*aA*(137,5)2, resuelves el coeficiente en el segundo miembro, y queda:
5025 = 9453,125*aA, divides en ambos miembros por 9453,125, y luego despejas:
aA ≅ 0,532 m/s2.
c)
Reemplaza el valor de la aceleración del móvil A y el valor del instante de encuentro, todo en la ecuación señalada (2), y queda:
vA ≅ 0,532*137,5 ≅ 73,091 m/s.
Reemplaza el valor del instante de encuentro, todo en la ecuación señalada (4), y queda:
vB = 0,32*137,5 = 44 m/s.
Espero haberte ayudado.