-
Hola me podrían ayudar con este ejercicio dice así..
Dos barcos salen simultáneamente de un puerto, uno viaja hacia el Sur a una velocidad de 30 km/h y el otro hacia el Este a una velocidad de 40 km/h. Después de dos horas ¿Cual es la velocidad de separación de los dos barcos?

Antonio Silvio Palmitano
el 5/8/19Considera un sistema de referencia con origen de coordenadas en el puerto, con eje OX en la dirección Oeste-Este, con sentido positivo hacia el Este, y con eje OY en la dirección Sur-Norte, con sentido positivo hacia el Norte, y con instante inicial: ti = 0 correspondiente a la salida de los barcos del puerto.
Luego, planteas la ecuación tiempo-posición de Movimiento Rectilíneo Uniforme para el primer barco (observa que se dirige hacia el Sur), y queda:
y = -30*t,
y observa que la expresión del punto donde se encuentra este barco en un instante genérico es:
A(0,-30*t),
y observa también que la expresión vectorial de su posición queda determinada por el vector OA, por lo que tienes:
p1 = < 0-0 , -30-0 >, resuelves componentes, y queda:
p1 = < 0 , -30*t > (1) (en Km).
Luego, planteas la ecuación tiempo-posición de Movimiento Rectilíneo Uniforme para el segundo barco (observa que se dirige hacia el Este), y queda:
x = 40*t,
y observa que la expresión del punto donde se encuentra este barco en un instante genérico es:
B(40*t, 0) (2),
y observa también que la expresión vectorial de su posición queda determinada por el vector OB, por lo que tienes:
p2 = < 40*t-0 , 0-0 >, resuelves componentes, y queda:
p2 = < 40*t , 0 > (2) (en Km).
Luego, planteas la expresión de la posición relativa del segundo barco con respecto al primero, y queda:
p2/1 = p2 - p1, sustituyes expresiones, y queda:
p2/1 = < 40*t , 0 > - < 0 , -30*t >, resuelves la resta entre vectores en el segundo miembro, y queda:
p2/1 = < 40*t , 30*t >, extraes el factor común escalar genérico (t), y queda:
p2/1 = < 40 , 30 >*t (3) (en Km);
luego, a partir de la expresión anterior señalada (3) (recuerda que los barcos se desplazan con Movimiento Rectilíneo Uniforme, por lo que la expresión vectorial de su posición es: p = v*t), tienes que la expresión de la velocidad relativa del segundo barco con respecto al primero es:
v2/1 = < 40 , 30 > (en Km/h).
Luego, planteas la expresión del módulo de esta velocidad relativa, y la rapidez relativa con que el segundo barco se aleja del primero queda expresada:
|v2/1| = √(402 + 302), resuelves el segundo miembro, y queda:
|v2/1| = 50 Km/h.
Espero haberte ayudado.
-
Hola alguien me puede ayudar con este verdadero o falso por favor sobre preguntas de teoricas de tiro parabolico, una de momento de inercia y otra de cuerpo rigido.
Marcar la respuesta CORRECTA para las siguientes preguntas.
1)En un tiro oblicuo sin considerar el rozamiento con el aire, se verifica que:
a)Para la misma altura, la rapidez en la etapa de descenso es el doble que en la etapa de ascenso.
b)La energía mecánica se conserva.
2)en un tiro oblicuo sin considerar el rozamiento con el aire, se verifica que:
a)La componente vertical de la velocidad se hace nula en el punto de máximo alcance horizontal.
b)La componente vertical de la velocidad se hace nula en el punto de máximo alcance vertical.
3)En un cuerpo en caída libre, despreciando el rozamiento con el aire:
a)La energía cinética es nula.
b)Las energías potencial y cinética coinciden.
c=La energía potencial es nula.
d)El trabajo del peso es positivo
Marcar la respuesta FALSA para las siguientes preguntas.
5)En un bloque de masa m en reposo apoyado sobre un plano inclinado de 30° respecto a la superficie horizontal se verifica que:
a)La fuerza normal y la componente vertical de la fuerza peso constituyen un par acción-reacción.
b)La fuerza normal y la fuerza de rozamiento dinámica tienen la misma magnitud.
c)La fuerza de rozamiento estática es nula.
d)El coeficiente de rozamiento estático es mayor que el coeficiente de rozamiento dinámico.
6)En un cuerpo lanzado verticalmente hacia arriba, despreciando el rozamiento con el aire, se verifica en cada instante que:
a)La energía cinética es nula.
b)La aceleración que actúa es conocida.
c)Las energías potencial y cinética coinciden.
d)El trabajo de la fuerza peso es positivo.
7)Todas las partículas de un cuerpo rígido que giran alrededor de un eje…
a) …giran el mismo ángulo en un tiempo dado.
b) … tienen la misma velocidad angular.
c) … comparten el mismo eje de rotación.
d) …recorren la misma distancia en un tiempo dado.
8)Una calesita de radio R y momento de inercia I gira con una velocidad angular Wi con una persona de masa m en reposo en el centro de la calesita. Si la persona comienza a moverse desde el centro hasta el borde entonces:
a)Se conserva el momento angular.
b)No se conserva la cantidad de movimiento.
c)El momento de inercia del sistema calesita-hombre irá disminuyendo.
d)La velocidad angular irá disminuyendo progresivamente.


Antonio Silvio Palmitano
el 5/8/19Vamos con una orientación, a ver si te ayudamos.
En las cuestiones que se refieren a movimiento vertical consideramos un sistema de referencia con eje de posiciones OY con dirección vertical, con sentido positivo hacia arriba, y con origen de coordenadas a nivel del suelo.
1)
a) Es Falsa, porque las rapideces son iguales para puntos que se encuentran a una misma altura.
b) Es Verdadera, porque no actúan fuerzas disipativas (rozamientos).
2)
a) Es Falsa, ya que la componente vertical es opuesta a la componente vertical de la velocidad en el instante de disparo.
b) Es Verdadera, ya que en este punto el proyectil "no sube ni baja", por lo que la componente vertical de su velocidad es igual a cero.
3)
a) Es Falsa, ya que la rapidez del móvil aumenta, y por lo tanto también aumenta su energía cinética.
b) Es Falsa, ya que la energía cinética aumenta y la energía potencial disminuye, y solo coinciden en un punto intermedio de la trayectoria del móvil.
c) Es Falsa, porque la energía potencial va disminuyendo a medida que cae el móvil, y solamente es igual a cero cuando de encuentra a nivel del suelo.
d) Es Verdadera, ya que el sentido del peso (hacia abajo) es igual al sentido de desplazamiento del móvil.
5)
a) Es Falsa, ya que las dos fuerzas están aplicadas sobre el cuerpo.
b) Es Falsa, ya que la magnitud de la fuerza de rozamiento estático es, como máximo, igual a la multiplicación del coeficiente de rozamiento estático por la magnitud de la fuerza normal que el plano inclinado ejerce sobre el cuerpo.
c) Es Falsa, porque si el rozamiento estático fuese nulo entonces el cuerpo deslizaría hacia abajo y no estaría en reposo.
d) Es Verdadera, ya que la fuerza necesaria para mover un cuerpo que está en reposo es la fuerza de rozamiento estático máximo, y su magnitud es menor que la magnitud d la fuerza de rozamiento dinámico que se debe vencer para mantenerlo en movimiento.
6)
a) Es Falsa, ya que la energía cinética es máxima en el punto de lanzamiento, y es igual a cero cuando el móvil alcanza su altura máxima.
b) Es Verdadera, ya que se trata de la aceleración gravitatoria terrestre.
c) Es Falsa, ya que en el punto de lanzamiento la energía cinética es máxima y la energía potencial es igual a cero, ya que la energía cinética es igual a cero en el punto de máxima altura y la energía potencial es máxima en dicho punto, por lo que solamente coincidirán los valores en un punto intermedio de la trayectoria del móvil.
d) Es Falsa, ya que el sentido del peso es hacia abajo, y es opuesto al sentido de desplazamiento del móvil.
7)
a) Es Verdadera.
b) Es Verdadera.
c) Es Verdadera.
d) Es Falsa, ya que la magnitud del arco descrito por cada punto depende de la rapidez angular (que es la misma para todos los puntos del cuerpo), y depende de la distancia entre el punto en estudio y el eje de rotación, que no es la misma para todos los puntos del cuerpo.
8)
a) Es Verdadera, ya que no actúan momentos de fuerzas exteriores al sistema calesita-persona.
b) Es Verdadera, ya que la cantidad de movimiento inicial de la persona es nula, pero no lo es cuando no se encuentra sobre el eje de rotación de la calesita.
c) Es Falsa, porque al inicio el momento de inercia de la persona con respecto al eje de giros es igual a cero, y luego aumenta a medida que la persona se aleja del mismo, mientras que el momento de inercia de la calesita permanece constante.
d) Es Verdadera, ya que la rapidez angular es inversamente proporcional al momento de inercia del sistema calesita-persona, ya que el momento angular de este sistema permanece constante.
Espero haberte ayudado.
-
Hola, alguien me puede ayudar con el siguiente problema, lo he intentado resolver pero mi respuesta no es correcta he intentado hallar el error pero no lo encuentro, adjunto una imagen de mis operaciones.

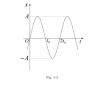
Problema: Un objeto se encuentra atado a un resorte que vibra con un movimiento armónico simple como el descrito en la imagen, t representa el tiempo y x la posición, encuentre la máxima velocidad para este movimiento.
-


Francisco Javier
el 2/8/19Todo el sistema esta en equilibrio. Por lo tanto, este problema se resuelve aplicando la primera ley de newton.
Del sistema cuerda-masa colocada a la derecha del todo de la imagen podemos realizar un análisis de fuerza vertical sencillo.
De este análisis sale que la tensión de la cuerda es igual al peso del bloque:
∑Fy = 0 → T - w = 0 → T = w = 1 kp
Ahora haciendo el análisis de fuerza vertical en la polea tenemos que:
2*T + T*Sin(45º) - F = 0
Y despejando para "F":
F = 2*T + T*Sin(45º)
F = 2*1 + 1*Sin(45º)
F = 2.7071 kp
-


Francisco Javier
el 1/8/19Asignamos como objeto "A" a la esfera de 300 kg.
Asignamos como objeto "B" a la esfera de 200 kg.
Usaremos el sub-indice "i" para designar todo lo que ocurra antes del choque.
Usaremos el sub-indice "f" para designar todo lo que ocurra después del choque.
Empezamos el problema determinando la velocidad máxima que alcanza la esfera "A" justo antes de chocar con la esfera "B".
Esto lo determinamos aplicando la conservación de la energía entre los puntos "x" y "y".
El punto "x" seria el lugar donde se suelta inicialmente la esfera "A". En este punto hay solo energía potencial y no hay cinética (vx = 0).
El punto "y" seria el lugar donde la esfera "A" esta justo por chocar la esfera "B". En este punto hay solo energía cinética y no hay potencial (hy = 0).
Recordamos que la energía cinética (K) y potencial (U) la determinamos respectivamente con las siguientes formulas:
K = 0.5*m*v2
U = m*g*h
Donde "m" es masa, "v" la velocidad, "g" la gravedad y "h" la altura.
La energía mecánica se define como la suma de la energía cinética y potencial en un punto:
E = K + U
Entonces con esto ya somos capaces de escribir las expresiones para la energía mecánica en los puntos "x" y "y":
Ex = Kx + Ux = 0.5*mA*vx2 + mA*g*hx
Para encontrar la altura "hx" hay que aplicar un poco de trigonometría.
Determinamos el cateto adyacente (CA) del péndulo respecto a su posición inicial:
Cos(θ) = CA/L
Donde "L" es la longitud de la cuerda. Despejando para "CA":
CA = L*Cos(θ)
Finalmente para obtener la altura en el punto "x" debemos restar el cateto adyacente a la longitud de la cuerda:
hx = L - L*Cos(θ) = L*[1 - Cos(θ)]
Reemplazando ahora esta altura en la energía mecánica en "x":
Ex = 0.5*mA*vx2 + mA*g*L*[1 - Cos(θ)] = 0.5*300*02 + 300*9.81*15*[1 - Cos(30º)] = 5 914.31 J
Hacemos lo mismo para el punto "y":
Ey = Ky + Uy = 0.5*mA*vy2 + mA*g*hy = 0.5*300*vy2 + 300*9.81*0 = 150*vy2
Ahora igualando las expresiones de energía mecánica en "x" y "y" (conservación de energía) hallamos la velocidad en "y":
5 914.31 = 150*vy2 → vy = 6.2792 m/s
Esta velocidad máxima es la que tendrá la esfera "A" justo antes de chocar con la esfera "B".
vy = vAi = 6.2792 m/s
Una vez calculada esta velocidad, hacemos el calculo de la altura para cada caso.
Caso #1: Choque elástico
Si se trata de un choque elástico, las esferas "A" y "B" después del choque dejan el sitio de colisión con diferentes velocidades y dirección.
En este caso, solo nos interesaría la velocidad de la esfera "B" después del choque.
Planteamos la velocidad de la esfera "B" después del choque (omitiendo demostración):
vBf = [(2*mA)/(mA + mB)]*vAi + [(mB - mA)/(mA + mB)]*vBi
Como la esfera "B" esta inicialmente en reposo, vBi = 0. Entonces:
vBf = [(2*mA)/(mA + mB)]*vAi = [(2*300)/(300+200)]*6.2792 = 7.5350 m/s
Finalmente, aplicamos conservación de energía nuevamente para hallar la altura máxima que alcanza la esfera "B".
0.5*mB*vBf2 = mB*g*hmax.
0.5*vBf2 = g*hmax.
0.5*7.53502 = 9.81*hmax.
hmax. = 2.8938 m
Caso #2: Choque inelastico
Si se trata de un choque inelastico, las esferas "A" y "B" después del choque quedan unidas con una misma velocidad.
Planteamos la velocidad en común para las esferas (omitiendo demostración):
vf = (mA*vAi + mB*vBi)/(mA + mB)
Como la esfera "B" esta inicialmente en reposo, vBi = 0. Entonces:
vf = (mA*vAi)/(mA + mB) = (300*6.2792)/(300+200) = 3.7675 m/s
Finalmente, aplicamos conservación de energía nuevamente para hallar la altura máxima que alcanza la esfera "B".
0.5*(mA + mB)*vf2 = (mA + mB)*g*hmax.
0.5*vf2 = g*hmax.
0.5*3.76752 = 9.81*hmax.
hmax. = 0.7234 m
-
Hola me pueden ayudar con el siguiente ejercicio, lo he intentado pero no puedo calcular la temperatura para así calcular el cambio de la energía interna sólo he podido calcular el trabajo realizado por el gas.
Un gas ideal monoatomico se expande de 100cm³ a 200 cm³ a una presión constante de 1x10⁵Pa. Calcule el cambio en la energía interna del gas
Gracias


Antonio Silvio Palmitano
el 1/8/19Vamos con una precisión.
Planteas la ecuación general de estado para gases ideales, y queda:
p*ΔV = n*R*ΔT, y de aquí despejas:
ΔT = p*ΔV/(n*R) (1).
Luego, planteas la expresión de la variación de energía interna, y queda:
ΔU = n*Cv*ΔT (2), aquí sustituyes la expresión señalada (1), simplificas, y queda:
ΔU = Cv*p*ΔV/R (3).
Luego, planteas la expresión de la variación de calor (recuerda que el proceso es isobárico, ya que la presión es constante), y queda:
ΔQ = n*Cp*ΔT (4).
Luego, planteas la ecuación correspondiente al Primer Principio de la Termodinámica, y queda:
ΔQ = ΔU + ΔW, sustituyes las expresiones señaladas (4) (2), y queda:
n*Cp*ΔT = ΔU + n*Cv*ΔT, restas n*Cv*ΔT en ambos miembros, extraes factores comunes en el primer miembro, y queda:
n*(Cp - Cv)*ΔT = ΔU, aplicas la relación entre calores específicos para gases ideales (Cp - Cv = R), y queda:
n*R*ΔT = ΔU, sustituyes la expresión señalada (1) en el tercer factor del primer miembro, y queda:
n*R*p*ΔV/(n*R) = ΔU, aquí simplificas, y luego despejas:
ΔU = p*ΔV, que es la igualdad que señala el colega Francisco Javier;
luego, sustituyes la expresión de la variación de volumen, y queda:
ΔU = p*(Vf - Vi), reemplazas valores (observa que empleamos unidades internacionales), y queda:
ΔU = 1*105*(2*10-4 - 1*10-4), resuelves, y queda:
ΔU = 10 J.
Espero haberte ayudado.
-
Ayúdenme ¡Por Favor!
Dos partículas, A y B son lanzadas simultáneamente. Si las Velocidades de A y B se diferencian en 5 m/s ¿Luego de qué tiempo estarán en una misma línea horizontal? 

Antonio Silvio Palmitano
el 1/8/19Planteas las ecuaciones de movimiento vertical para ambos móviles (consideramos un sistema de referencia con eje de posiciones OY vertical con sentido positivo hacia arriba, con origen de coordenadas a nivel del punto de lanzamiento de los móviles, y con instante inicial: ti = 0 correspondiente al lanzamiento de los mismos), cancelas términos nulos, y queda:
yA = vA*t - (1/2)*g*t2,
yB = vB*t - (1/2)*g*t2;
luego, restas miembro a miembro (observa que tienes cancelaciones), extraes factor común, y queda:
yA - yB = (vA - vB)*t;
luego, planteas la condición de posiciones iguales para los móviles (yA = yB, y observa que ésta condición implica la anulación del primer miembro de la ecuación), y queda:
0 = (vA - vB)*t,
divides por (vA - vB) en ambos miembros, y queda:
0 = t,
por lo que puedes concluir que los dos móviles tendrán la misma posición solamente en el instante de lanzamiento.
Espero haberte ayudado.