-
Tengo una discursion con unos amigos y el caso es que yo digo que si tiro un ''baso de tubo de cristal'' (400g aprox.)desde un avion y cae sobre una playa de arena suabe no se rompe y ellos dicen que si ** Yo pienso que no porque el viento lo frena y no cae con la suficiente fuerza como para romperse** ayudadme porfavor!!!!! Jajjajja
-
En el vídeo del péndulo dice que este describe un movimiento armónico simple.
Pero... ¿en el eje horizontal, vertical o ambos?
muchas gracias y un saludo


Antonio Silvio Palmitano
el 9/8/19En el péndulo matemático, y con oscilaciones de amplitud muy pequeña, tienes que la trayectoria del móvil se encuentra sobre un arco de circunferencia muy pequeño, por lo que se acepta considerarlo como un segmento (trozo de recta), que está incluido en el eje OX, que en este caso es horizontal, con origen de coordenadas en el punto de equilibrio (o centro de oscilación), y, además, se define un eje OY vertical con sentido positivo hacia arriba, sobre la recta en la que se encuentra el hilo cuando el móvil se encuentra en su posición de equilibrio.
Espero haberte ayudado.
-
os dejo otro problema el apartado a si lo he sacado pero en el apartado b, cuando voy a sustitur el coeficiente de rozamiento para sacar la FN y poder seguir sustituyendo en la ecuacion, al ser el valor 0..... como algo dividido por 0 no da nada, me sale error, entonces la respuesta para el apartado b es que no puede no haber un coeficiente de rozamiento con valor 0 ¿no ? gracias por la ayuda que me podais dar. saludos.




Antonio Silvio Palmitano
el 9/8/19a)
Observa que sobre el bloque m están aplicadas dos fuerzas, de las que indicamos sus módulos, direcciones y sentidos:
Peso: Pm = m*g, vertical, hacia abajo;
Tensión de la cuerda: T, vertical, hacia arriba;
luego, aplicas la Primera Ley de Newton (consideramos un eje OY vertical con sentido positivo hacia arriba), y queda la ecuación:
T - Pm = 0, aquí sustituyes la expresión del módulo del peso, y luego despejas: T = m*g (1).
Observa que sobre el bloque m0 están aplicadas dos fuerzas, de las que indicamos sus módulos, direcciones y sentidos:
Peso: P0 = m0*g, vertical, hacia abajo;
Acción normal del bloque M: NMm0, vertical, hacia arriba;
luego, aplicas la Primera Ley de Newton (consideramos un eje OY vertical con sentido positivo hacia arriba), y queda la ecuación:
NMm0 - P0 = 0, aquí sustituyes la expresión del módulo del peso, y luego despejas: NMm0 = m0*g (2).
Observa que sobre el bloque m0 están aplicadas cuatro fuerzas, de las que indicamos sus módulos, direcciones y sentidos:
Peso: PM = M*g, vertical, hacia abajo;
Reacción normal del bloque m0: NMm0, vertical, hacia abajo;
Acción normal de la superficie de apoyo: NM, vertical, hacia arriba;
Tensión de la cuerda: T, horizontal, hacia la derecha;
Rozamiento estático máximo de la superficie de apoyo: fre = μe*NM, horizontal, hacia la izquierda;
luego, aplicas la Primera Ley de Newton (consideramos un eje OX horizontal con sentido positivo hacia la derecha, y un OY vertical con sentido positivo hacia arriba), y queda el sistema de ecuaciones:
T - fre = 0,
NM - NMm0 - PM = 0,
sustituyes expresiones en ambas ecuaciones, y queda:
T - μe*NM = 0 (3),
NM - NMm0 - M*g = 0 (4);
y solo queda que sustituyas las expresiones señaladas (1) (2) en las ecuaciones señaladas (3) (4), para luego resolver el sistema (te dejo la tarea).
b)
Observa que si no tienes rozamiento entre la superficie de apoyo y el bloque M, entonces tienes que el sistema está acelerado, ya que no existen fuerzas que equilibren a la tensión de la cuerda. Además, si no tienes rozamiento entre el bloque M y el bloque m0, entonces tienes que sobre este último no están aplicadas fuerzas horizontales, por lo que tienes que este bloque permanece en reposo, y solo se desplazan los bloques m y M; pero, si sí tienes rozamiento entre ellos, entonces tienes que existe la posibilidad que el sistema esté acelerado, pero con los bloques M y m0 desplazándose juntos.
Espero haberte ayudado.
-
Hola, se trata de un problema de palancas.
Me gustariá saber en que me he podido confundir para que el signo de la Fuerza normal que se pide en el apartado d no me de con el mismo signo que la solución que da la profesora en el problema. A mi me ha salido con signo - , por lo que que el sentido de esa fuerza en la palanca sería hacia abajo. entonces al darme (-) entiendo que se trata de una palanca de tipo 3 . pero en las soluciones podréis ver que sale +, asi que no se en la ecuación de Fuerza total donde me he podido confundir...gracias por la info que me podais dar. Saludos
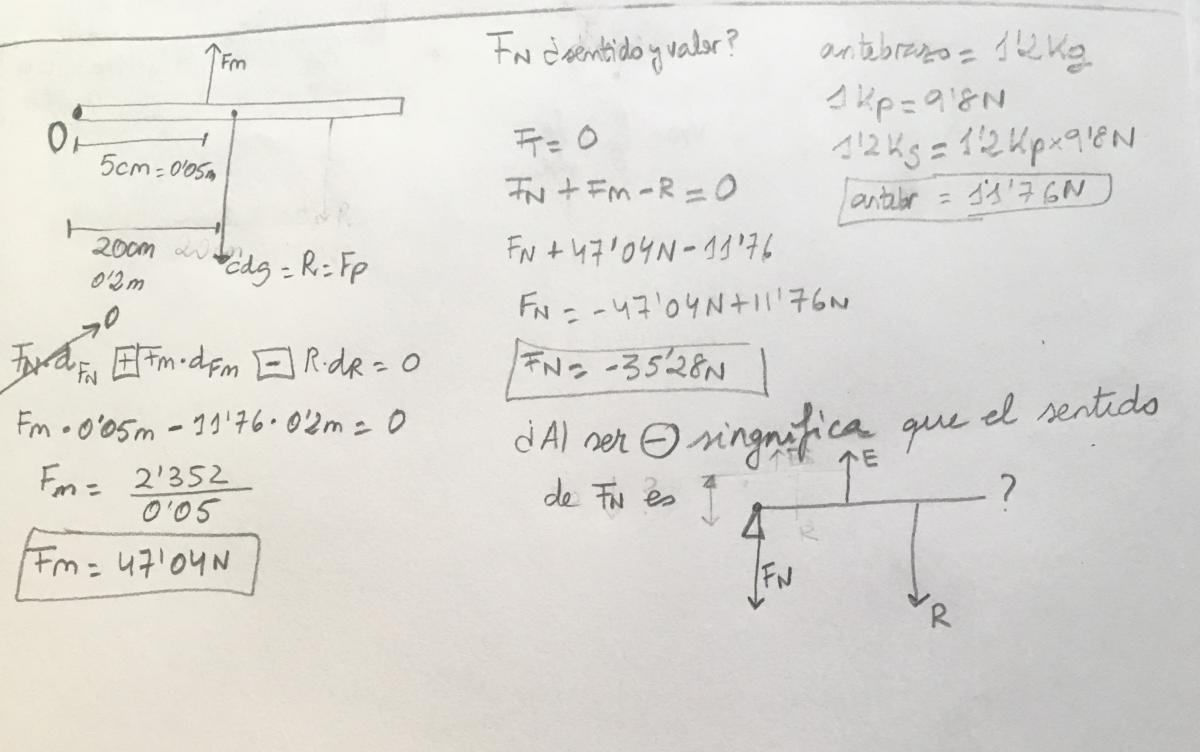



Antonio Silvio Palmitano
el 9/8/19Considera un sistema de referencia con eje OX horizontal con sentido positivo hacia la derecha, con eje OY vertical con sentido positivo hacia arriba, con origen de coordenadas en el punto O y con sentido de giro positivo antihorario, todo según tu figura.
Luego, observa que sobre el antebrazo tienes aplicadas tres fuerzas, de las que indicamos sus módulos, direcciones, sentidos, y brazos de momento con respecto al punto O:
Peso: P = M*g = 1,2*9,8 = 11,76 N, vertical, hacia abajo, dP = 20 cm = 0,2 m;
Fuerza muscular: Fm, vertical, hacia arriba, dFm = 5 cm = 0,05 m;
Acción normal del punto de apoyo: FN, vertical, suponemos por el momento que hacia arriba, dFN = 0.
Luego, aplicas la Primera Ley de Newton (para traslaciones, y también para giros), y queda:
FN + Fm - P = 0,
+dFm*Fm - dP*P + dFN*dFn = 0;
luego, sustituyes las expresiones de los módulos de las fueras y de los brazos de momento, y queda:
FN + Fm - 11,76 = 0 (1),
+0,05*Fm - 0,2*11,76 + 0*dFn = 0 (2);
luego, resuelves términos y cancelas el término nulo en la ecuación señalada (2), y queda:
+0,05*Fm - 2,352 = 0, de aquí despejas:
Fm = 2,352/0,05, resuelves, y queda:
Fm = 47,04 N;
luego, reemplazas el valor remarcado en la ecuación señalada (1), y queda:
FN + 47,04 - 11,76 = 0, reduces términos numéricos, y queda:
FN + 35,28 = 0, restass 35,28 en ambos miembros, y queda:
FN = -35,28 N,
y observa que el signo negativo solamente te indica que el sentido que hemos supuesto para esta fuerza (recuerda que supusimos que era hacia arriba) no es el correcto, sino que su sentido es hacia abajo.
Observa que si hubiésemos supuesto desde un principio que el sentido de esta fuerza era hacia abajo, entonces cambiarían todos los signos de los términos correspondientes a ella, y el sistema cuyas ecuaciones hemos señalado (1) (2) quedaría:
-FN + Fm - 11,76 = 0 (1),
+0,05*Fm - 0,2*11,76 - 0*dFn = 0 (2);
y hubiésemos llegado a un resultado positivo, que sería: FN = +35,28 N.,
y el módulo de la fuerza muscular hubiese quedado expresado: Fm = 47,04 N.
Espero haberte ayudado.
-
Buenas, me gustaría saber porqué utiliza la primera masa cuando N=P si es a la segunda masa a la que se le aplica la fuerza



Antonio Silvio Palmitano
el 8/8/19A ver si te ayudo con este desarrollo un poco más detallado.
Establece un sistema de referencia con eje OX horizontal con sentido positivo hacia la derecha, y con eje OY vertical con sentido positivo hacia arriba, según tu imagen.
Luego, observa que sobre el bloque señalado (1) están aplicadas tres fuerzas, de las que indicamos sus módulos, direcciones y sentidos:
Peso: P1 = M1*g, vertical, hacia abajo;
Acción normal del bloque señalado (2): N12, vertical, hacia arriba;
Rozamiento estático máximo del bloque (2): fre12 = μe*N12, horizontal, hacia la derecha;
luego, aplicas la Segunda Ley de Newton, y tienes el sistema de ecuaciones:
fre12 = M1*a,
N12 - P1 = 0;
luego, sustituyes las expresiones de los módulos de las fuerzas, y queda:
μe*N12 = M1*a,
N12 - M1*g = 0, de aquí despejas: N12 = M1*g;
luego, sustituyes esta última expresión remarcada en la primera ecuación, y queda:
μe*M1*g = M1*a, aquí divides por M1 en ambos miembros, y luego despejas: a = μe*g.
Luego, observa que sobre el bloque señalado (2) están aplicadas cinco fuerzas, de las que indicamos sus módulos, direcciones y sentidos:
Peso: P2 = M2*g, vertical, hacia abajo;
Reacción normal del bloque señalado (1): N12, vertical, hacia abajo;
Acción normal del suelo: N2, vertical, hacia arriba;
Reacción al rozamiento estático máximo del bloque (1): fre12 = μe*N12, horizontal, hacia la izquierda;
Fuerza externa aplicada: F, horizontal, hacia la derecha;
luego, aplicas la Segunda Ley de Newton, y tienes el sistema de ecuaciones:
F - fre12 = M2*a,
N2 - N12 - P2 = 0;
luego, sustituyes las expresiones de los módulos de las fuerzas aplicadas sobre el bloque señalado (2), y queda:
F - μe*N12 = M2*a,
N2 - N12 - M2*g = 0;
luego, sustituyes las expresiones del módulo de la acción-reacción normal mutua de los bloques, y del módulo de la aceleración del conjunto formado por los dos bloques, que tienes remarcadas, y queda:
F - μe*M1*g = M2*μe*g, y de aquí despejas: F = μe*(M1 + M2)*g,
N2 - M1*g - M2*g = 0, y de aquí despejas: N2 = (M1 + M2)*g.
Espero haberte ayudado.
-
 Me gustaría saber si el ejercicio está correctamente solucionado o también haría falta realizarlo cuando el bloque baja, el enunciado es el siguiente:
Me gustaría saber si el ejercicio está correctamente solucionado o también haría falta realizarlo cuando el bloque baja, el enunciado es el siguiente:Desde la base de un plano inclinado 45°, se lanza hacia arriba un bloque con una cierta velocidad inicial. Sube hasta un punto y regresa al punto inicial. Si el tiempo de bajada es el doble del tiempo de subida, halle el coeficiente dinámico de fricción entre el bloque y el plano.


Antonio Silvio Palmitano
el 16/8/19Consideramos para el ángulo de 45°: cos(45°) = 0,71 y sen(45°) = 0,71; y consideramos que el módulo del desplazamiento del bloque sobre el plano es L.
Luego, vamos con un planteo por etapas.
1°)
El bloque asciende por la rampa (observa que la fuerza de rozamiento es paralela a la rampa con sentido hacia abajo).
Estableces un sistema de referencia con instante inicial: ti = 0 correspondiente al inicio del movimiento de ascenso del bloque, con eje OX paralelo a la rampa con sentido positivo hacia arriba, y con eje OY perpendicular a la rampa con sentido positivo hacia arriba.
Luego, observa que sobre el bloque están aplicadas tres fuerzas, de las que indicamos sus módulos, direcciones y sentidos:
Peso: P = M*g, vertical, hacia abajo;
Acción normal de la rampa: N, perpendicular a la rampa, hacia arriba;
Rozamiento dinámico de la rampa, fr = μ*N, paralela a la rampa, hacia abajo;
luego, aplicas la Segunda Ley de Newton, y queda el sistema de ecuaciones:
-P*sen(45°) - fr = M*a1,
N - P*cos(45°) = 0;
luego, resuelves el sistema (te dejo la tarea), y queda:
N = 0,71*M*g,
a1 = -0,71*(1+μ)*g;
luego, planteas la ecuación velocidad-desplazamiento de Movimiento Rectilíneo Uniformemente Variado, y queda:
v2 - vi2 = 2*a1*Δx, aplicas la condición de llegada al punto más alto (v = 0), y queda:
-vi2 = 2*a1*Δx, sustituyes la expresión de la aceleración y del módulo del desplazamiento, y queda:
-vi2 = -1,42*(1+μ)*g*L, multiplicas en ambos miembros por -1, y queda:
vi2 = 1,42*(1+μ)*g*L (*);
luego, planteas la ecuación tiempo-velocidad de Movimiento Rectilíneo Uniformemente Variado, y queda:
v = vi + a1*t1, aplicas la condición de llegada al punto más alto (v = 0), y queda:
0 = vi + a1*t1, restas a1*t1 en ambos miembros, y queda:
-a1*t1 = vi, multiplicas por -1 en ambos miembros, y queda:
a1*t1 = -vi, sustituyes la expresión de la aceleración, resuelves signos, y queda:
0,71*(1+μ)*g*t1 = vi, elevas al cuadrado en ambos miembros, resuelves, y queda:
0,50*(1+μ)2*g2*t12 = vi2, sustituyes la expresión del primer miembro en la ecuación señalada (*), y queda:
0,50*(1+μ)2*g2*t12 = 1,42*(1+μ)*g*L, divides en ambos miembros por 0,50*(1+μ)*g, y queda:
(1+μ)*g*t12 = 2,82*L (1).
2°)
El bloque desciende por la rampa (observa que la fuerza de rozamiento es paralela a la rampa con sentido hacia arriba).
Estableces un sistema de referencia con instante inicial: ti = 0 correspondiente al inicio del movimiento de descenso del bloque, con eje OX paralelo a la rampa con sentido positivo hacia abajo, y con eje OY perpendicular a la rampa con sentido positivo hacia arriba.
Luego, observa que sobre el bloque están aplicadas tres fuerzas, de las que indicamos sus módulos, direcciones y sentidos:
Peso: P = M*g, vertical, hacia abajo;
Acción normal de la rampa: N, perpendicular a la rampa, hacia arriba;
Rozamiento dinámico de la rampa, fr = μ*N, paralela a la rampa, hacia arriba;
luego, aplicas la Segunda Ley de Newton, y queda el sistema de ecuaciones:
P*sen(45°) - fr = M*a2,
N - P*cos(45°) = 0;
luego, resuelves el sistema (te dejo la tarea), y queda:
N = 0,71*M*g,
a2 = 0,71*(1-μ)*g;
luego, planteas la ecuación tiempo-desplazamiento de Movimiento Rectilíneo Uniformemente Variado, cancelas términos nulos, y queda:
Δx = (1/2)*a2*t22, sustituyes la expresión del módulo del desplazamiento, y queda:
L = (1/2)*a2*t22, sustituyes la expresión de la aceleración, y queda:
L = 0,355*(1-μ)*g*t22,
sustituyes la expresión del intervalo de tiempo en función de su correspondiente en la etapa de ascenso que tienes en tu enunciado, y queda:
L = 0,355*(1-μ)*g*(2*t1)2, resuelves la potencia, resuelves el coeficiente, y queda:
L = 1,42*(1-μ)*g*t12 (2).
3°)
Sustituyes la expresión señalada (2) en la ecuación señalada (1), y queda:
(1+μ)*g*t12 = 2,82*1,42*(1-μ)*g*t12, resuelves el coeficiente en el segundo miembro, y queda:
(1+μ)*g*t12 = 4*(1-μ)*g*t12, divides por g*t12 en ambos miembros, y queda:
1 + μ = 4*(1 - μ), distribuyes el segundo miembro, y queda:
1 + μ = 4 - 4*μ, sumas 4*μ y restas 1 en ambos miembros, y queda:
5*μ = 3, divides por 5 en ambos miembros, y queda:
μ = 3/5 = 0,6.
Espero haberte ayudado.
-
Esta bien resuelto?? Sino es así como sería?
Que altura habría que ascender en la atmósfera para que la presión atmosférica descienda 1mm de Hg?


Antonio Silvio Palmitano
el 8/8/19Has expresado correctamente a la variación de la presión atmosférica en Pascales:
Δp = 1 mm(Hg) = 101300/760 ≅ 133,289 Pa.
Luego, tienes el valor de la densidad de masa del aire, y observa que debes corregir su valor expresado en unidades internacionales:
δai = 1,3 g/L = 1,3 g/dm3 = 1,3*0,001/0,001 = 1,3 Kg/m3.
Luego, planteas la expresión de la variación de presión en función de la variación de altura, y queda:
δai*g*Δh = Δp,
divides en ambos miembros por δai y por g, y queda:
Δh = Δp/(δai*g),
reemplazas valores, y queda
Δh ≅ 133,289/(1,3*9,8) ≅ 10,462 m.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 7/8/19Establece un sistema de referencia con origen de coordenadas a nivel del suelo, con eje de posiciones (alturas) OY con dirección vertical y sentido positivo hacia arriba.
Luego, tienes los datos iniciales:
M = 5 Kg (masa del móvil),
yi = 20 m (posición inicial del móvil)
vi = 0 (rapidez inicial del móvil, que suponemos parte desde el reposo),
g = 9,8 m/s2 (módulo de la aceleración gravitatoria terrestre);
luego, planteas la expresión de la energía mecánica inicial del móvil, y queda:
EMi = EPgi + ECti, sustituyes las expresiones de la energía potencial gravitatoria y de la energía cinética de traslación, y queda:
EMi = M*g*yi + (1/2)*M*vi2, aquí cancelas el último término (observa que es igual a cero), y queda:
EMi = M*g*yi (1).
Luego, tienes los datos del instante en estudio:
ya = 5 m (posición del móvil),
va = a determinar (rapidez del móvil);
luego, planteas la expresión de la energía mecánica del móvil en este instante, y queda:
EMa= EPga + ECta, sustituyes las expresiones de la energía potencial gravitatoria y de la energía cinética de traslación, y queda:
EMa = M*g*ya + (1/2)*M*va2 (2).
a)
Planteas la expresión de la variación de energía potencial gravitatoria del móvil, y queda:
ΔEPg = EPga - EPgi, sustituyes las expresiones de las energías potenciales, y queda:
ΔEPg = M*g*ya - M*g*yi, extraes factores comunes, y queda:
ΔEPg = M*g*(ya - yi), reemplazas valores, y queda:
ΔEPg = 5*9,8*(5 - 20), resuelves, y queda:
ΔEPg = -735 J, y observa que el signo negativo señala que ha disminuido la energía potencial gravitatoria del móvil.
b)
Observa que no se consideran las fuerzas disitpativas (rozamientos), y observa también que no están aplicadas fuerzas externas que aporten energía al móvil, por lo que planteas conservación de la energía mecánica, y queda la ecuación:
EMa = EMi, sustituyes las expresiones señaladas (2) (1), y queda:
M*g*ya + (1/2)*M*va2 = M*g*yi, multiplicas por 2 y divides por M en todos los términos, y queda:
2*g*ya + va2 = 2*g*yi, restas 2*g*ya en ambos miembros, y queda:
va2 = 2*g*yi - 2*g*ya, extraes factores comunes en el segundo miembro, y queda:
va2 = 2*g*(yi - ya), extraes raíz cuadrada positiva en ambos miembros, y queda:
va = √( 2*g*(yi - ya) ), aquí reemplazas valores, y queda:
va = √( 2*9,8*(20 - 5) ), resuelves, y queda:
va = √(294) m/s ≅ 17,146 m/s,
c)
Tienes los datos del nuevo instante en estudio:
yc = 0 (el móvil está a punto de chocar contra el suelo),
vc = a determinar (rapidez del móvil en este instante);
luego, planteas la expresión de la energía mecánica del móvil en este instante, y queda:
EMc= EPgc + ECtc, sustituyes las expresiones de la energía potencial gravitatoria y de la energía cinética de traslación, y queda:
EMc = M*g*yc + (1/2)*M*vc2, cancelas el primer término de esta expresión (observa que es igual a cero), y queda:
EMc = (1/2)*M*vc2 (3);
luego, planteas conservación de la energía, y queda la ecuación:
EMc = EMi, sustituyes las expresiones señaladas (3) (1), y queda:
(1/2)*M*vc2 = M*g*yi, multiplicas por 2 y divides por M en ambos miembros, y queda:
vc2 = 2*g*yi, extraes raíz cuadrada positiva en ambos miembros, y queda:
vc = √(2*g*yi), aquí reemplazas valores, y queda:
vc = √(2*9,8*20), resuelves, y queda:
vc = √(392) m/s ≅ 19,799 m/s.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 6/8/19Establece un sistema de referencia con eje OX horizontal, con sentido positivo acorde al desplazamiento del cuerpo, y con eje OY vertical, con sentido positivo hacia arriba.
Observa que sobre el cuerpo están aplicadas cuatro fuerzas, de las que indicamos sus módulos, direcciones y sentidos:
Peso: P = M*g, vertical, hacia abajo;
Acción normal de la mesa: N, vertical, hacia arriba;
Fuerza exterior aplicada: F, horizontal, según el semieje OX positivo;
Rozamiento dinámico de la mesa: frd = μd*N, horizontal, según el semieje OX negativo.
a)
Aplicas la Primera Ley de Newton (observa que el cuerpo se desplaza con velocidad constante), y queda el sistema de ecuaciones:
F - frd = 0, y de aquí despejas: F = frd,
N - P = 0, y de aquí despejas: N = P;
luego, sustituyes las expresiones de los módulos de la fuerza de rozamiento dinámico y del peso del cuerpo, y queda:
F = μd*N,
N = M*g = 5*9,8 = 49 N;
luego, reemplazas el valor de módulo de la acción normal que tienes remarcado, reemplazas el valor del coeficiente dinámico que tienes en tu enunciado, todo en la primera ecuación, y queda:
F = 0,4*49 = 19,6 N,
y observa que la fuerza externa aplicada es exactamente la opuesta a la fuerza de rozamiento dinámico, por lo que tienes que el módulo de esta última fuerza es:
frd = 19,6 N.
b)
Observa que el sentido de la fuerza exterior y el sentido del desplazamiento del cuerpo coinciden, por lo que el trabajo realizado por dicha fuerza queda expresado:
WF = F*Δx*cos(0°) = reemplazas valores = 19,6*1,5*1 = 29,4 J.
Observa que el sentido de la fuerza de rozamiento dinámico y el sentido del desplazamiento del cuerpo son opuestos, por lo que el trabajo realizado por dicha fuerza queda expresado:
Wfrd = frd*Δx*cos(180°) = reemplazas valores = 19,6*1,5*(-1) = -29,4 N.
Observa que la dirección del peso es perpendicular a la dirección del desplazamiento del cuerpo, por lo que el trabajo realizado por dicha fuerza queda expresado:
WP = P*Δx*cos(90°) = reemplazas valores = 49*1,5*0 = 0.
Observa que la dirección de la acción normal es perpendicular a la dirección del desplazamiento del cuerpo, por lo que el trabajo realizado por dicha fuerza queda expresado:
WN = N*Δx*cos(90°) = reemplazas valores = 49*1,5*0 = 0.
Luego, planteas la expresión del trabajo total realizado sobre el cuerpo, y queda:
WT = WF + Wfrd + WP + WN, reemplazas valores, y queda:
WT = 29,4 + (-29,4) + 0 + 0 = 0,
y puedes apreciar que el trabajo resultante realizado sobre el cuerpo es igual a cero, ya que la energía cinética de traslación del cuero permanece constante (recuerda que se desplaza con velocidad constante), y la energía potencial gravitatoria también es constante (recuerda que el cuerpo se desplaza sobre una superficie horizontal), por lo que tienes que la energía mecánica total del cuerpo permanece constante.
Espero haberte ayudado.
-
Hola, sé que es un problema largo y por lo menos para mi se ha vuelto muy complicado si alguien se toma el tiempo de ayudarme se lo agradecería muchísimo.
Un bloque P de masa M está en un plano horizontal liso, y un objeto Q de masa m siempre está encima del bloque P. Inicialmente, tanto P como Q están en reposo. En un tiempo t = 0, se da una velocidad inicial v0 a P en la dirección hacia la derecha.Entonces Q también comienza a moverse. Cuando se pasa un tiempo T después de que P recibe una velocidad inicial, la velocidad de P coincide con la velocidad de Q. Un coeficiente de fricción cinética entre P y Q se denota como µ. Trate la dirección hacia la derecha como positiva, y la aceleración de la gravedad se denota como g. Responde las siguientes preguntas.
(1) Encuentre la fuerza que actúa sobre Q en el tiempo t (0 <t <T).
(2) Encuentre la fuerza que actúa sobre P en el tiempo t (0 <t <T).
(3) Encuentre la velocidad de P en el tiempo t (0<t<T).
(4) Encuentre la expresión de T usando algunas otras cantidades adecuadas.
(5) Encuentre la distancia que Q se movió contra P en la duración de t = 0 a t = T.He intentado varias cosas pero en realidad no he logrado nada relevante


Antonio Silvio Palmitano
el 6/8/19Vamos con una orientación.
Observa que sobre el bloque P están aplicadas cuatro fuerzas, de las que indicamos sus módulos, direcciones y sentidos:
Peso: PP = MP*g, vertical, hacia abajo;
Acción normal del suelo: NS, vertical, hacia arriba;
Acción normal del bloque Q: NQP, vertical, hacia abajo;
Fuerza exterior que produce el desplazamiento: F, horizontal, hacia la derecha;
Rozamiento estático del bloque Q: freQP, horizontal hacia la izquierda;
luego, estableces un sistema de referencia OXY usual, aplicas la Segunda Ley de Newton, y tienes las ecuaciones:
F - freQP = MP*a (1),
NS - NQP - PP = 0 (2),
Observa que sobre el bloque Q están aplicadas tres fuerzas, de las que indicamos sus módulos, direcciones y sentidos:
Peso: PQ = MQ*g, vertical, hacia abajo;
Reacción normal del bloque P: NQP, vertical, hacia arriba;
Reacción al rozamiento estático dle bloque P: freQP, horizontal, hacia la derecha;
luego, estableces un sistema de referencia OXY usual, aplicas la Segunda Ley de Newton, y tienes las ecuaciones:
freQP = MQ*a (3),
NQP - PQ = 0 (4).
Observa que hemos considerado que los dos bloques se desplazan juntos en todo momento, por eso es que hemos planteado que se ejercen mutuamente una fuerza de rozamiento estático, ya que no habría desplazamiento de uno de los bloques con respecto al otro.
Luego, considera el instante inicial: ti = 0, planteas la expresión de la aceleración de Movimiento Rectilíneo Uniformemente Variado, y queda:
a = (VT - V0)/(T - 0), cancelas el término nulo en el denominador, y queda:
a = (VT - V0)/T (5).
Luego, planteas la ecuación velocidad-desplazamiento de Movimiento Rectilíneo Unformemente Variado (consideramos que la posición inicial es: xi = 0), y queda:
VT2 -V02 = 2*a*(xT - 0), cancelas el término nulo en el agrupamiento del segundo miembro, y queda:
VT2 -V02 = 2*a*xT (6).
Luego, con las seis ecuaciones numeradas tienes todo lo que es necesario para responder las cuestiones de tu enunciado.
Haz el intento de terminar la tarea, y si te resulta necesario no dudes en volver a consultar.
Espero haberte ayudado.

















