-
Juan Olvedo
el 19/9/16
-
ana fierro
el 19/9/16Necesito ayuda con este problema:
SI tenemos un bloque de pisos con 50 pisos, y al mes los inquilinos pagan 300Euros, se llenan. Por tanto tenemos la oportunidad de subir el precio,pero por cada 10euros mas de un piso, perdemos un inquilino, cual es la oferta que debemos hacer para salir ganando???????
graxx
César
el 19/9/16La ganancia vendra definida por el numero de inquilinos * precio del piso
nº inquilinos 50-x
precio 300+10x , luego G(x)=(50-x)( 300+10x) si hallamos sus extremos .
Derivando G´(x)=10(x+30)(50-x)=0 Tiene un máximo en x=10 y G(x)=16000
Luego cuando se tienen 40 inquilinos y se les cobra 400 euros
-
Marco
el 19/9/16
por favor ayudenme, con los 3 es por un examen que quiero apelar.
Antonio Silvio Palmitano
el 19/9/16En el primer ejercicio puedes separar variables y queda:
(1/y)*dy = tan(2x)* dx, por identidad trigonométrica el segundo miembro queda:
(1/y)*dy = ( sen(2x) )/( cos(2x) )*dx
Luego integramos en ambos miembros, y observa que la integral de la izquierda es directa, y que la integral de la derecha se resuelve con la sustitución (cambio de variable): w = 2x, lo haces y queda:
ln|y| = (-1/2)*ln|cos(2x)| + C
que es una solución general implícita de la ecuación diferencial.
En el tercero haces pasaje de término y queda:
dy/dx = x*(2y - 3)/(x^2 + 1)
luego separas variables y queda:
( 1/(2y - 3) )*dy = ( x/(x^2 + 1) )*dx
observa que para integrar a la izquierda puedes proponer la sustitución: w = 2y - 3, y que para integrar a la derecha puedes proponer la sustitución: z = x^2 + 1, resuelves y queda:
(1/2)*ln|2y - 3| = (1/2)*ln(x^2 + 1) + C
multiplicamos en todos los términos por 2, escribimos K en lugar de 2C y queda:
ln|2y - 3| = ln(x^2 + 1) + K
que es una solución general implícita de la ecuación diferencial.
En el segundo ejercicio. Si la consigna es derivar implícitamente con respecto a x lo hacemos y queda:
3x^2 * y^2 + 2x^3*y*y ' - x^(-2) - y^(-2) * y ' = 0
hacemos pasajes de términos y queda:
2x^3*y*y ' - y^(-2) * y ' = - 3x^2 * y^2 + x^(-2)
extraemos factor común a la izquierda y queda:
( 2x^3*y - y^(-2) )* y ' = - 3x^2 * y^2 + x^(-2)
hacemos pasaje de factor como divisor y queda:
y ' = ( - 3x^2 * y^2 + x^(-2) )/( 2x^3*y - y^(-2) )
que es la expresión de la derivada de y en forma implícita, con las aclaraciones: el denominador es distinto de cero, x es distinto de cero e y es distinto de cero.
Espero haberte ayudado.
-
Marco
el 19/9/16 -
Marco
el 19/9/16ayuda por favor con estos ejercicios
ana fierro
el 19/9/16AYUDAME A MI POR FAVOR
SI tenemos un bloque de pisos con 50 pisos, y al mes los inquilinos pagan 300Euros, se llenan. Por tanto tenemos la oportunidad de subir el precio,pero por cada 10euros mas de un piso, perdemos un inquilino, cual es la oferta que debemos hacer para salir ganando???????
David
el 20/9/16Llamamos x al numero de veces que incrementamos el precio 10€... Si subimos el precio 10€, x=1... Si subimos el precio 20€, x=2... Si subimos el precio 30€, x=3....
El precio del apartamento será 300 + 10x...
Ese valor de x coincidirá además con el numero de inquilinos perdidos... y por tanto los inquilinos reales serán 50-x...
El precio recaudado será (300+10x)(50-x)=15000-300x+500x-10x²=15000+200x-10x² y debes comprobar cuando será mayor que 50.300=15000€....
Por tanto, resuelve 15000+200x-10x² > 15000.... 200x-10x²>0... Es una inecuacion de segundo grado, de solucion (0,20) te sugiero este video.... Inecuaciones de segundo grado
La mayor ganancia coincide con el vertice de la funcion cuadratica -10x²+200x, que es x=10... Te sugiero... Representacion funcion cuadratica
Si x=20, los inquilinos serán 30 y el precio 300+10.20=300+200=500€...y ganaremos 30.500=15000€...
Si x=21, los inquilinos serán 29 y el precio 300+10.21=300+210=510€...y ganaremos 29.510=14790€...
Si x=19, los inquilinos serán 31 y el precio 300+10.19=300+190=490€...y ganaremos 31.490=15190€...
Si x=1, los inquilinos serán 49 y el precio 300+10.1=300+10=310€...y ganaremos 49.310=15190€...
Si x=2, los inquilinos serán 48 y el precio 300+10.2=300+20=320€...y ganaremos 48.320=15360€...
Si x=10, los inquilinos serán 40 y el precio 300+10.10=300+100=400€...y ganaremos 40.400=16000€... -
LOLA
el 19/9/16Calcular la serie de Taylor de la función e ^ x, centrada en el cero, es fácil:
La serie de Taylor de e^x centrada en el cero = ∑ (desde n = 0 hasta infinito) de (x^n)/n!
pero como puedo comprobar que la serie evaluada en x coincide con e^x para todo x perteneciente a los numeros reales.
Un saludo.
Antonio Silvio Palmitano
el 19/9/16Puedes plantear el cociente entre el término general de orden (n+1) con el término general de orden n, y queda:
( x^(n+1) / (n+1)! ) / ( x^n / n! ) = ( n! / (n+1)! )*( x^(n+1) / x^n ) = ( 1 / (n+1) )*x
Luego, puedes aplicar el criterio del cociente (o de la razón), calculando el límite cuando n tiende a infinito del valor absoluto del cociente que nos quedó:
Lím(n-->+inf) | ( 1 / (n+1) )*x | = Lín(n-->+inf) ( 1 / (n+1) )*|x| = |x| * Lím(n-->+inf) ( 1 / (n+1) ) = |x|*0 = 0 < 1, para todo valor de x perteneciente a los reales, por lo que el intervalo de convergencia es (-inf,+inf), por lo que la serie representa a la función en el conjunto de los números reales.
Espero haberte ayudado.
-
razexx
el 19/9/16Buenas Tardes Unicoos,9)
Me gustaría que alguien me resolviese y explicase como resolver este ejercicio (demostración por inducción). Lo necesito para mañana.
[IMG]https://drive.google.com/open?id=0B5CpBbY6Hp7IQm5fdWJJcElEeDg[/IMG]Gracias de antemano. Un saludo
Antonio Silvio Palmitano
el 19/9/16P(1): a = (a - a^2)/(1 - a) = a(1 - a)/(1 - a) = a, por lo que tenemos que la proposición para n = 1 es Verdadera.
P(h): a + a^2 + ... + a^n = (a - a^(n+1))/(1 - a), para todo h >= 1, h perteneciente al conjunto de los números naturales (Hipótesis Inductiva)
P(h+1): a + a^2 + ... + a^n + a^(n+1) = ( a - a^(n+2) )/(1-a), que debemos demostrar (Tesis Inductiva)
Demostración:
P(h+1): a + a^2 + ... + a^n + a^(n+1) = a + a^2 + ... + a^n + a^(n+1) = agrupamos términos = ( a + a^2 + ... + a^n ) + a^(n+1) = aplicamos la Hipótesis Inductiva =
= (a - a^(n+1))/(1 - a) + a^(n+1) = extraemos denominador común = ( a - a^(n+1) + (1 - a)*a^(n+1) )/(1-a) = distribuimos en el numerador =
= ( a - a^(n+1) + a^(n+1) - a*a^(n+1) )/(1-a) = cancelamos términos opuestos y resolvemos el último término en el numerador =
= ( a - a^(n+2) )/(1-a).
Por lo tanto, de acuerdo al Axioma de Inducción (5° Axioma de Peano) hemos demostrado:
P(1) es Verdadera
P(h) --> P(h+1) es Verdadera
por lo tanto concluimos que P(n) es Verdadera para todo n perteneciente al conjunto de los números naturales, con n mayor o igual que uno.
Espero haberte ayudado.
-
Antonio
el 19/9/16Límites infinitésimos
Hola Unicoos, estoy calculando límites y me acaba de salir uno en un ejercicio que es 1-cos^2x.
En la fórmula de límites infinitésimos dice que 1-cos=X^2/2
Qué hago??? elevo x^2/2 al cuadrado??
-
Keith Caballero Rodriguez
el 19/9/16Me pueden ayudar con este problema
chado
el 19/9/16no se bien cual seria tu duda exacmente.
lo que si te pued decir de antemano es que deberias de definir la funcion F como una funcion por partesprimero te quedaria asi por definicion de modulo para [x+2]
(x+2)-[x-3] x>=-2(-x-2)-[x-3] x<-2
pero ahora deberias de de aplicar de nuevo la definicion pero para [x-3]
(x+2)-(x-3) x>=-2 ^ x>=3
(x+2)-(-x+3) x>=-2 ^ x<3
(-x-2)-(x-3) x<-2 ^ x>=3
(-x-2)-(-x+3) x<-2 ^ x<3
de aca podrias continuar fijandote donde esta definida g para poder hacer la composición -
Abigail Rojas
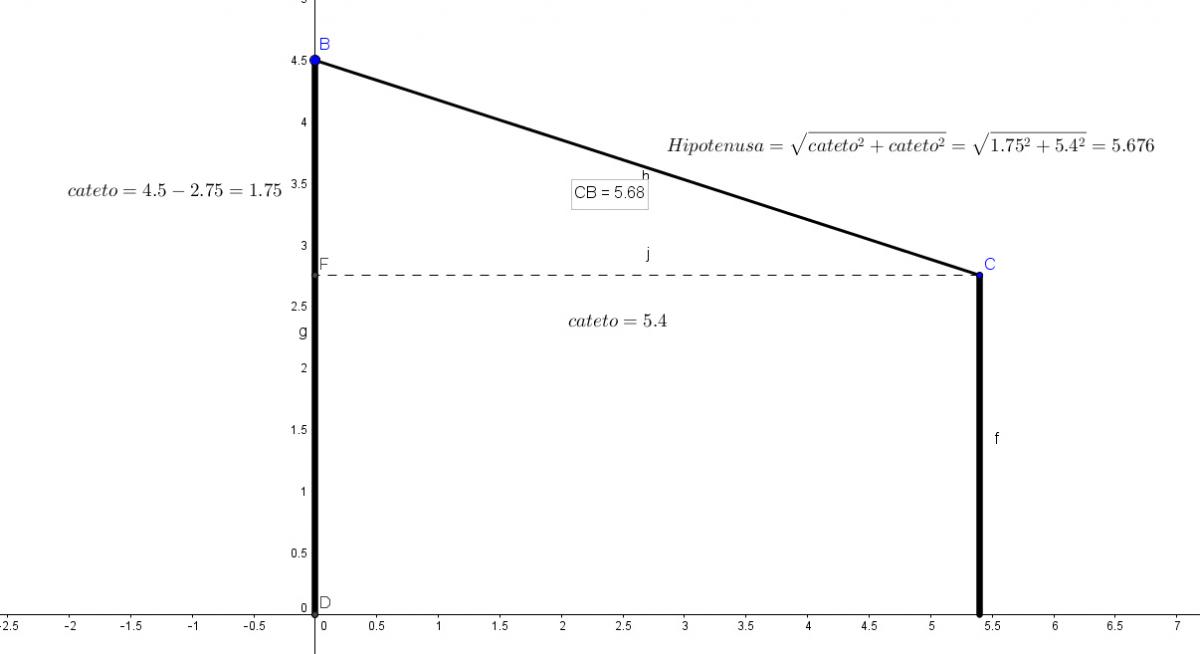
el 19/9/16Por favor ayuda!!!! dos muros paralelos están separados por una distancia de 5 metros y 40 centimetros. Si sus alturas son de 4.5 metros y 2.75 metros respectivamente¿cual será el tamaño mínimo de la viga que se colocará entre estos dos muros?
