-
Hola a todos, alguien me ayuda con estos limites?? El primero no se si lo tengo bien resuelto y en el segundo...me he atascado...gracias de antemano
-
Hola unicoos por favor ayuda con este ejercicio me falta el paso intermedio para llegar a la solución particular.


Antonio Silvio Palmitano
el 8/7/16Observa que has cometido un error al separar variables:
el integrando para y tiene denominador V(1+ y^2)., y esta integral la puedes resolver con la sustituicón (cambio de variable) w = y^2 + 1, de la que tenemos dw = 2y*dy, de donde tenemos que (1/2)*dw = y*dy, ahora sustituyes y la integral para y queda:
(1/2)*Integral (1/V(w) * dw) = V(w) + C = V(1 + y^2) + C.
La integral para x la has resuelto correctamente, por lo que la solución general implícita queda:
V(1 + y^2) = (3/2) * x^2 + C.
Ahora a partir de la condición inicial, reemplazamos 1 para x y V(8) para y, y queda:
3 = 3/2 + C, de donde obtenemos: C = 3/2.
Por lo tanto, la solución particular implícita queda:
V(1 + y^2) = (3/2) * x^2 + 3/2, que también puede expresarse:
V(1 + y^2) = (3/2) *(x^2 + 1)
Para obtener la solución particular explícita, elevamos al cuadrado en ambos miembros (observa que a la derecha de la igualdad puedes distribuir) y queda:
1 + y^2 = (9/4) * (x^2 + 1)^2.
Luego hacemos un pasaje de término y queda:
y^2 = (9/4) * (x^2 + 1)^2 - 1
Y por último hacemos pasaje de potencia como raíz, y de acuerdo con la condición inicial elegiremos la raíz cuadrada positiva ya que y>0:
y = +V((9/4) * (x^2 + 1)^2 - 1)
Espero haberte ayudado.
-
Hola unicoos, estoy repasando ejercicios de vectores con soluciones y en este tengo una duda, no sé porque a la z le pone el valor 0 y 1.


Antonio Silvio Palmitano
el 8/7/16Debes tener muy en cuenta que la intersección de los dos planos que se corresponden al sistema de dos ecuaciones inicial, es una recta, que a su vez es un conjunto de infinitos puntos.
Observa que con dos ecuaciones se ha podido despejar x y también y, pero no se pudo despejar z, por lo que z puede tomar cualquier valor real (z ha qudado "libre").
Y para identificar dos puntos de la recta, simplemente se eligen dos valores para z, y en este caso han elegido z = 0, y z = 1 (observa que podrían haber elegido cualquier otro par de números reales). Con ellos obtienen dos puntos de la recta, y a partir de ellos obtienen finalmente las componentes del vector director de la recta.
Espero haberte ayudado.


Antonius Benedictus
el 8/7/16Una recta en el espacio viene expresada como intersección de dos planos; algebraicamente, una recta viene dada como un sistema lineal de dos ecuaciones y tres incógnitas, compatible indeterminado con un grado de libertad (una incógnita libre). Si ésta resulta ser "z", para obtener puntos de la recta, asignas a z distintos valores, resolviendo después el sistema en las incógnitas x,y.
-
Hola unicoos, pueden de favor enviarme algunas imagenes resueltas de integrales resueltas en donde el proceso seaaa largo, integrales dificiles. Gracias.


chado
el 9/7/16Integral TRIGONOMÉTRICA con cambio de variable TANGENTE 02
Integral de secx (SECANTE)
y hay mas en el canal de youtube. busca bien. te van a servir -
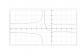
Aquí la he pintado, la normal y el valor absoluto. He pintado f(x) en negra en rojo valor absoluto de f(x), pero no sé pintar f de valor absoluto de x. La pregunta esta abajo. No tengo ni idea de lo que me preguntan. Necesito ayuda.


Antonio Silvio Palmitano
el 8/7/16Observa que si x es positivo, tienes que |x|=x, pero si x es negativo, tienes que |x|= -x. Entonces:
si x es positivo: f(|x|) = f(x) y la gráfica se mantiene para x>=0,
pero si x es negativo: f(|x|) = f(-x) (observa que -x es positivo), por lo tanto la gráfica toma los el valor de su opuesto, lo equivale a decir que la parte de la gráfica que se encuentra a la derecha del eje x se refleja con respecto al eje y, y debes trazar a al izquierda de dicho eje una gráfica simétrica (recuerda las funciones pares, para las que se cumple que f(x) = f(-x).
Espero haberte ayudado. -
hola, me podéis ayudar?. Sé que la de valor absoluto se hace pasando lo que este debajo del eje y al eje x. Pasando lo negativo a positivo, pero y la otra como se hace?. No tengo ni idea. Gracias.
-
Hola, ¿podéis ayudarme con el siguiente ejercicio de números complejos?
Si z es un número complejo, resuelve en C la ecuación: z²+8=0

Antonio Silvio Palmitano
el 8/7/16Primero hacemos pasaje de término y queda:
z^2 = -8
Luego, si representamos gráficamente al número compejo real -8, verás que se corresponde con el punto de coordenadas (-8,0), que se encuentra en el semieje x (real) negativo, a una distancia de 8 unidades del origen, por lo que su módulo es igual a 8, y su argumento, medido desde el semieje positivo x es 180° (o pi radianes).
Ahora, si escribimos en forma polar (módulo y argumento), la ecuación queda:
z^2 = [8](180°)
Luego hacemos pasaje de potencia como raíz y queda:
z = V([8](180°))
Luego, a partir de la fórmula de De Moivre para las raíces tenemos que:
z = [V(8)]((180° + k*360°)/2), con k = 0 o k = 1.
Por lo tanto, las dos soluciones quedan:
para k = 0:
z = [V(8)](90°)
para k = 1:
z = [V(8)](270°)
Las dos quedan expresadas en forma polar, y puedes luego expresarlas en forma trigonométrica o binómica, u otra que te pidan con las fórmulas de pasaje que seguramente has visto en clase.
Espero haberte ayudado.








_Thumb.jpg)




_Thumb.jpg)

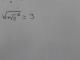

_Thumb.jpg)