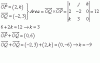-
-
Sean L1 : x − 2y = 3 , L2 : −2x + y = −3 y L3 : X = α.(1, −7).
a) Dar una ecuación paramétrica de la recta L que pasa por el punto de intersección de L2
y L3 y es paralela a L1 .
b) Dar una ecuación implícita de la recta L prima que pasa por el punto de intersección de L1 y
L2 y es perpendicular a L3 .
-


Jose Ramos
el 21/12/19Está bien, porque la solución que te da es: (x,y,z,t) = (1, -1,1,1) + μ (-3,-2,3,1). Veamos quien es f (x, y, z,t) = f(1,-1,1,1) + μ f(-3,-2,3,1) = f(1, -1, 1, 1) + μ (0,0,0,0) porque (-3,-2,3,1) era base del núcleo. Entonces llegamos a que:
f(x,y,z,t) = f(1, -1,1,1) = (3,5,2,4), por tanto todas tus soluciones son antiimagenes de (3,5,2,4) mediante f.