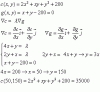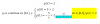-


Antonio Silvio Palmitano
el 23/12/19Tienes la expresión de la función:
P(m,n) = 4,5*m + 5*n - 0,5*m2 - n2 - 0,25*m*n,
y observa que la función es diferenciable para todo valor de las variables independientes m y n.
Luego, planteas las expresiones de las funciones derivadas parciales primeras, y queda:
Pm(m,n) = 4,5 - m - 0,25*n (1),
Pn(m,n) = 5 - 2*n - 0,25*m (2).
Luego, planteas las expresiones de las funciones derivadas parciales segundas, y queda:
Pmm(m,n) = -1 < 0,
Pmn(m,n) = -0,25,
Pnm(m,n) = -0,25,
Pnn(m,n) = -2,
y observa que las cuatro expresiones son continuas para todo valor de m y de n.
a)
Planteas la condición de punto estacionario (posible máximo o posible mínimo) de la función, y queda el sistema de ecuacioens:
Pm(m,n) = 0,
Pn(m,n) = 0,
sustituyes las expresiones señaladas (1) (2), y queda:
4,5 - m - 0,25*n = 0,
5 - 2*n - 0,25*m = 0,
restas 4,5 en ambos miembros de la primera ecuación, restas 5 en ambos miembros de la segunda ecuación, y queda:
-m - 0,25*n = -4,5,
-2*n - 0,25*m = -5,
multiplicas por -4 en todos los términos de ambas ecuaciones, ordenas términos en las egunda ecuación, y queda:
4*m + n = 18, de aquí despejas: n = 18 - 4*m (3)
m + 8*n = 20;
luego, sustituyes la expresión señalada (3) en la segunda ecuación, distribuyes su segundo término, reduces términos semejantes, y queda:
-31*m + 144 = 20, restas 144 en ambos miembros, luego divides por -31 en ambos miembros, y queda: m = 4 h;
luego, reemplazas este último valor remarcado en la ecuación señalada (3), resuelves, y queda: n = 2 h.
Luego, tendrías que evaluar las expresiones de las funciones derivadas segundas para los valores críticos remarcados, pero observa que esta tarea no es necesaria, ya que las cuatro derivadas parciales segundas son constantes;
luego, planteas la expresión del discriminante hessiano para los valores estacionarios, y queda:
H(4,2) = Pmm(4,2)*Pnn(4,2) - Pmn(4,2)*Pnm(4,2), reemplazas valores, y queda:
H(4,2) = (-1)*(-2) - (-0,25)*(-0,25), resuelves, y queda:
H(4,2) = 1,9375 > 0;
luego, según el Criterio de las Derivadas Segundas, tienes que la función alcanza un Máximo para los valores estacionarios remarcados, dado que el discriminante hessiano toma un valor positivo para ellos, y que la función derivada parcial segunda toma un valor negativo.
b)
Evalúas la expresión de la función para los valores estacionarios que tienes remarcados, y queda:
P(4,2) = 4,5*4 + 5*2 - 0,5*42 - 22 - 0,25*4*2, resuelves en cada término, y queda:
P(4,2) = 18 + 10 - 8 - 4 + 2, resuelves, y queda:
P(4,2) = 18, que es el valor máximo que alcanza la función.
Espero haberte ayudado.
-
Dar una ecuación implícita del plano Π que contiene a las rectas transversales L : X =
λ.(1, 2, −1) + (3, 0, 0) y L prima
: X = λ.(−2, −4, 1) + (5, 4, −3).
 quisiera saber si esta bien,busque la interseccion,y realize el producto vectorial de ambos vectores directores,mi pregunta es si no es necesario buscar la interseccion para hallar D,si un punto de paso de la recta ya es suficiente al estar contendida en el plano ambas rectas,y quisiera saber por que el producto vectorial de ambos vectores directores me da la normal del plano,desde ya gracias.
quisiera saber si esta bien,busque la interseccion,y realize el producto vectorial de ambos vectores directores,mi pregunta es si no es necesario buscar la interseccion para hallar D,si un punto de paso de la recta ya es suficiente al estar contendida en el plano ambas rectas,y quisiera saber por que el producto vectorial de ambos vectores directores me da la normal del plano,desde ya gracias.

Antonio
el 23/12/19Efectivamente, no hace buscar el punto de intersección de ambas rectas, podrías haber usado cualquier punto de cualquiera de las dos rectas,
por ejemplo usar el (3,0,0)
con respecto a la otra pregunta decirte que el producto vectorial de dos vectores es un vector perpendicular a ambos vectores
-
Si L : X = α.(k^2 + 1, k, k + 7) + (0, 2, 1) y Π : x + 2y − 3z = 2 , determinar todos los
valores de k para los que L y Π son paralelos. Quisiera saber si esta bien y si es la unica forma de resolverlo?.



Jose Ramos
el 23/12/19Lo tienes bien, tan solo cuando das el resultado debes cambiar el símbolo ∧ por el ∨ (ya que se trata de que k = - 4 ó k = 5 ) pues ∧ indica conjunción, es decir que se den las dos igualdades a la vez, lo cual es imposible.
También lo puedes hacer de otro modo con las ecuaciones cartesianas de la recta y haciendo que el sistema formado por la recta y el plano sea incompatible:
-
(5-20x) exp^-x=2 ns como resolver la equacion
Derivada de 3200ln(0.02x+1)=3200x0.02/0.02x+1 resultado del profe
Y yo encuentro 3200/0.02x+1 ns de dónde saca el 0.02 del numerador.he utilizado u'v+uv'
-
buenas alguien puede ayudarme a sacar la derivada de:
∫(2x-7)/(2x²-14x+20)