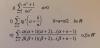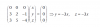-
Buen día. Tengo que calcular el volumen de una región W tridimensional comprendida por la gráfica de la función f(x,y)=e^(x2 + y^2) y la región D = {(x,y) E R^2: 1≤ x^2 + y^2 ≤ 2}. Ya expresé a W en coordenadas cilíndricas de la siguiente manera
W = { (r, θ, z) E R^3 / √1≤ r ≤ √2; 0 ≤ θ ≤ 2π; 0 ≤ z ≤ e^(r^2)}
Ahora tengo que plantear la triple integral para poder calcular W. Pero no se que función integrar. Me podrían dar una mano?


Antonio Silvio Palmitano
el 24/12/19Vas muy bien.
Has planteado correctamente el cambio a coordenadas cilíndricas de eje OZ, has planteado correctamente los intervalos de integración, y recuerda que el factor de compensación (Jacobiano) es: |J| = r.
Luego, planteas la expresión cartesiana del volumen comprendido entre la gráfica de una función que toma valores positivos y una región E del plano coordenado OXY, y queda:
V = ∫∫∫E 1*dx*dy*dz;
luego, planteas el cambio a coordenadas cilíndricas, y la integral queda (recuerda que debes introducir el factor de compensación):
V = 0∫2π1∫√(2)0∫e^r^2 1*r*dz*dr*dθ,
resuelves la integral para la variable z (te dejo los pasos), y queda:
V = 0∫2π1∫√(2) er^2*r*dr*dθ,
y aquí observa que puedes aplicar la sustitución (cambio de variable): w = r2 para resolver la integral para la variable r, para luego continuar la tarea.
¡Haz el intento! Y si te resulta necesario, no dudes en volver a consultar.
Espero haberte ayudado.
-
Buenos dias y Feliz Navidad!
¿Alguien podría decirme por qué no consigo hallar el lugar geométrico de los puntos del espacio tales que su distancia al plano x-y=0 y al punto (4,0,0) sea la misma?
No se calcula en ninguna web, y al intentar graficar la solución que yo obtengo [x2+y2+2xy+2z2=-32] no se obtiene ninguna.
Gracias
-
Buenas tardes, quería saber bien si esta ecuación (H2 x K/a2 =(3x ∝)/3 p (a)) Esta bien escrita. Es “La ecuación de la evolución o evolutividad de Nowak”. Lo de la izquierda, representa las cadenas de moléculas, los de la derecha, presiones de selección y índice de adaptación. Significa que para que la vida surja, solo se necesita moléculas sujetas a fuerza de selección y mutación. Si existen esas condiciones, hay autorreplicación. ¿Pero no sé si está bien escrita o no? Pido mil disculpas por tu tiempo. Agradecería si pueden ayudarme.


Breaking Vlad
el 8/1/20Hola Alejandra, esta pregunta correspondería más bien a un foro de biología.
Puesto que en unicoos no tenemos puedes visitar: https://www.beunicoos.com
Un saludo,
Vlad
-
De 4000 familias con 4 niños. ¿Cuántas calcula deben tener:
a) Al menos un niño?.
P(X mayor igual a 1) 1-P(x<1) = 1- C4,0*0.5^0*0.5^4= 0.9744
b) 2 niños?:
P(x=2) C4,2*0.5^2*0.5^2= 0.375
c) Una o dos niñas?:


Jose Ramos
el 23/12/19El enunciado supongo que será: "De 4000 familias con 4 hijos. ¿Calcula... etc.
c) Una o dos niñas es el mismo suceso que tres o dos niños, por lo tanto, dado que X es "nº de niños", tenemos que es P (X=2)+P(X=3) = C4,2*0,5^2*0,5^2 + C4,3 ^0,5^3*0,5 = 6.0,5^4 + 4. 0,5^4 = 0,5^4. 10 = 10/16 = 0,625. ¿Cuántas familias?.- 4000. 0,625 = 2500
-
Dar una ecuación implícita del plano Π que contiene a las rectas paralelas L : X =
λ.(1, 2, −1) + (3, 0, 0) y L prima
: X = λ.(−2, −4, 2) + (0, 1, 1).
c) ¿Existe algún plano que contenga simultáneamente a las rectas L : X = λ.(1, 2, 0) +
(3, 0, −3) y L prima
: X = λ.(−2, 0, 0) + (0, 2, 3) ?