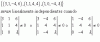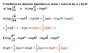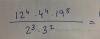-
Si me piden determinar λ para que la familia {(3,1,-4,6),(1,1,4,4),(1,0,-4,λ)} sea linealmente dependiente, el valor de lambda va a ser siempre el mismo sin importar el determinante que haga? Por qué?


Jose Ramos
el 25/12/19No es casualidad. Si el problema tiene solución, como en este caso, el valor del parámetro siempre ha de ser el mismo sea cual sea el menor de orden 3 que tomes. Supón que para un determinante lambda da 1 y para otro lambda da 8. Esto querría decir que el rango de la matriz formada por los tres vectores es 3 (el rango es el número de vectores linealmente independientes), pues cuando lambda es 1 te anula un determinante, pero no te anula el que da lambda 8. Y viceversa para lambda 8. Espero haberme explicado...
-
Hola unicoos, ¡feliz Navidad!
Si nos encontramos ante la ecuación x²-1=0, es obvio que para hallar los valores que puede tomar la x para satisfacer la igualdad se haría x=±√1.
Ahora imaginen que tenemos la ecuación z²-1-i=0 ==> z²=1+i ==> ¿z=±√(1+i)? o ¿z=√(1+i) a secas?
Planteo esta pregunta por esto que he leído:
-
hola, me podrías ayudar con este castillo de potencias???
12 elevado a 4 por 4 elevado a 4 por 19 elevado a 8 todo ello partido entre 2 elevado a 3 por 3 elevado a 2.
he factorizado en potencias de base 2 y 3 todo excepto el 19 ( que es primo) y no se qué hacer con él.
Me podrían ayudar ???
Gracias y Feliz Navidad !!!!
-
¿Si es posible le podríais echar un vistazo al siguiente ejercicio (adjunto documento) ? Gracias y que tengáis feliz navidad:
Transforma los siguientes logaritmos en sumas y restas de log A y log B: