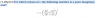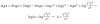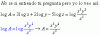-
Alguien me puede ayudar a solucionar esto?
Perdón, el resultado final lo he puesto fatal, quizás n son fracciones...
-


Breaking Vlad
el 3/2/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-


Antonio Silvio Palmitano
el 3/2/20Tienes la ecuación diferencial:
dy/dt = -k*y, separas variables, y queda:
dy/y = -k*dt, integras en ambos miembros, y queda:
Ln(y) = -k*t + a (1);
luego, evalúas la ecuación señalada (1) para la condición inicial: t = 0, y = C, sustituyes, resuelves, cancelas el término nulo, y queda:
Ln(C) = a, sustituyes esta expresión en la ecuación señalada (1), y queda:
Ln(y) = -k*t + Ln(C), restas Ln(C) en ambos miembros, y queda:
Ln(y) - Ln(C) = -k*t, aplicas la propiedad del logaritmo de una división, y queda:
Ln(y/C) = -k*t, compones en ambos miembros con la función exponencial natural, y queda:
y/C = e-k*t, multiplicas por C en ambos miembros, y queda:
y = C*e-k*t (2),
que es la expresión de la solución general de la ecuación diferencial de tu enunciado.
Luego, tienes la condición correspondiente a la administración del material al paciente: t = 24 h, y = 5 mCi,
reemplazas estos valores en la ecuación señalada (2), reemplazas el valor del coeficiente k que tienes en tu enunciado, y queda la ecuación:
5 = C*e-0,1155*24, resuelves el exponente, y queda:
5 = C*e-2,772, multiplicas en ambos miembros por e2,772, y queda:
5*e2,772 = C, resuelves el primer miembro, y luego despejas:
C ≅ 79,953 mCi,
que es la cantidad de material producida, que es la cantidad que se debe solicitar, a fin de recibir la cantidad de material adecuada para administrarle al paciente.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 3/2/20Considera un sistema de referencia con eje OX paralelo a la superficie de agua, con dirección y sentido positivo acordes al desplazamiento del bloque, y con eje OY vertical con sentido positivo hacia arriba.
Luego, observa que sobre el conjunto bote-pasajero están aplicadas cuatro fuerzas: Peso, Empuje, Fuerza del motor y Fuerza de resistencia, por lo que aplicas la Segunda Ley de Newton, y quedan las Ecuaciones:
F - FR = M*a (1),
E - P = 0, de aquí despejas: E = P, o sea: E = 320 + 160, resuelves, y queda: E = 480 lb.
Luego, sustituyes las expresiones de la fuerza de resistencia y de la aceleración en función de la velocidad y del tiempo, y queda:
F - k*v = M*dv/dt,
expresas a la masa en función del peso y del módulo de la aceleración gravitatoria terrestre (g = 32 p/s2), y queda:
F - k*v = (P/g)*dv/dt, multiplicas por g en todos los términos, y queda:
g*F - g*k*v = P*dv/dt, reemplazas datos, y queda:
32*50 - 32*k*v = 480*dv/dt, resuelves el primer miembro, y queda:
1600 - 32*k*v = 480*dv/dt, divides por 32 en todos los términos, y queda:
50 - k*v = 15*dv/dt, separas variables, y queda:
dt = 15*dv/(50 - k*v), multiplicas por -k en amos miembros, y queda:
-k*dt = 15*[-k*dv/(50 - k*v)], integras en ambos miembros, y queda:
-k*t + C = 15*Ln(50 - k*v) (2).
Luego, tienes en tu enunciado: v = 20 p/s, FR = 40 lb, reemplazas valores, y la expresión del módulo de la fuerza de resistencia queda:
40 = k*20, y de aquí despejas: k = 2 lb*s/p, reemplazas ese ultimo valor en la ecuación señalada (2), y queda:
-2*t + C = 15*Ln(50 - 2*v) (3).
Luego, puedes considerar el instante inicial: ti = 0 correspondiente a la velocidad vi = 0 (observa que el conjunto bote-pasajero parte desde el reposo), reemplazas estos valores en la ecuación señalada (3), y queda:
-2*0 + C = 15*Ln(50 - 2*0), resuelves términos, cancelas el término nulo, y queda: C = 15*Ln(50);
luego, reemplazas este último valor en la ecuación señalada (3), y queda:
-2*t + 15*Ln(50) = 15*Ln(50 - 2*v), restas 15*Ln(50) en ambos miembros, extraes factor común, y queda:
-2*t = 15*[Ln(50 - 2*v) - Ln(50)], aplicas la propiedad del logaritmo de una división, y queda:
-2*t = 15*Ln([50 - 2*v]/50), distribuyes el denominador en el argumento del logaritmo, y queda:
-2*t = 15*Ln(1 - 0,04*v), divides por 15 en ambos miembros, y queda:
-(2/15)*t = Ln(1 - 0,04*v), compones en ambos miembros con la función exponencial natural, y queda:
e-(2/15)*t = 1 - 0,04*v, multiplicas por 25 en todos los términos, y queda:
25*e-(2/15)*t = 25 - v, y de aquí despejas:
v = 25 - 25*e-(2/15)*t (4),
que es la expresión de la velocidad del conjunto bote-pasajero en función del tiempo.
a)
Planteas el límite para t tendiendo a +infinito de la expresión señalada (4), resuelves (te dejo la tarea), y queda:
vL = 25 p/s,
que es la expresión de la velocidad límite que alcanza el conjunto bote-pasajero.
b)
Expresas a la velocidad en función de la posición y del tiempo en la ecuación remarcada y señalad (4), y queda:
dx/dt = 25 - 25*e-(2/15)*t, separas variables, y queda:
dx = (25 - 25*e-(2/15)*t)*dt, integras en ambos miembros, y queda:
x = 25*t + (375/2)*e-(2/15)*t + D, resuelves el coeficiente en el segundo término, y queda:
x = 25*t + 187,5*e-(2/15)*t + D (5);
luego, evalúas la ecuación señalada (5) para la condición inicial: ti = 0, xi = 0, resuelves términos, cancelas términos nulos, y queda:
0 = 187,5 + D, y de aquí despejas: D = -187,5;
luego, reemplazas este último valor en la ecuación señalada (5), y queda:
x = 25*t + 187,5*e-(2/15)*t - 187,5.
Espero haberte ayudado.
-
 4ºESO. Adjunto un ejercicio de logaritmos que he realizado. En la solución he incluido la parte del ejercicio que no termino de entender, concretamente la IMPLICACIÓN que se hace en el solucionario del libro de que el argumento (A) es igual al logaritmo (x³y²/z⁵). De ser así ¿no significaría eso que el logaritmo (cociente x³y²/z⁵) equivale a 1→A¹=A? Espero no haberme liado con la explicación. Si así fuera, por favor comentar. Muchas gracias por la ayuda.
4ºESO. Adjunto un ejercicio de logaritmos que he realizado. En la solución he incluido la parte del ejercicio que no termino de entender, concretamente la IMPLICACIÓN que se hace en el solucionario del libro de que el argumento (A) es igual al logaritmo (x³y²/z⁵). De ser así ¿no significaría eso que el logaritmo (cociente x³y²/z⁵) equivale a 1→A¹=A? Espero no haberme liado con la explicación. Si así fuera, por favor comentar. Muchas gracias por la ayuda.