-
Harvey
el 24/8/17
Hola amigos unicoos ,recurro a ustedes nuevamente esta vez a pedir ayuda en estos 3 ejercicios. He pasado horas intentando llegar a las solución pero no lo logro. Me estoy frustrando y rindiendo no se que hacer.
David
el 28/8/17Una ecuacion de segundo grado (del tipo ax²+bx+c=0) tiene:
-Dos soluciones reales si b²-4ac>0
-Doble solucion si b²-4ac=0-no tiene solucion si b²-4ac<0...
Por tanto debes aplicar eso en tus ejercicios.
Por ejemplo, en el primero a=1, b=-k y c=k-1...
Por tanto, por ejemplo, tendrá doble solucion si (-k)²-4.1.(k-1)=0
Conociendo además la formula de las ecuaciones de segundo grado, la solucion será nula si -b = b²-4ac... De nuevo sustituyendo a,b,c tendrás una ecuacion
Por otro lado, debes conocer las formulas de Vieta... x1+x2=-b/a x1. x2 =c/a
Si una solucion es el doble de la otra, llamando "x" a una solucion e "y" a la otra.....y=2x .....
Sustituyendo en las formulas de vieta... x+2x=-b/a... 3x= -b/a
sustituyendo en la otra ... x.2x=c/a... 2x²=c/a... Como conoces a,b,c, al sustituir te quedará un sistema de dos ecuaciones con dos incognitas (x,k)....
Fórmulas de Vieta
¿Nos cuentas que obtuviste paso a paso despues? Animo! -
lbp_14
el 24/8/17Hola Unicoos,
Para que una recta pase por un punto y corte a dos rectas, por qué hay que contener en un plano al punto y a la recta? No lo visualizo. Qué pasa si no las contienes en un plano? Me lo pueden explicar detalladamente. Muchísimas gracias.
Martín Ramírez
el 24/8/17Este video puede ayudarte:
Recta que pasa por un punto y corta otras dos rectas
En todo caso si quiere definirse una recta (r) que se corte con dos rectas dadas (a y b) y pase por un punto dado (P):
- Se determina el punto de intersección (I), de la recta (a) con el plano (a) definido por la recta (b) y el punto (P)
- La recta (r), que se corta con las rectas (a y b), queda definida por los puntos (P e I)
La siguiente imagen muestra a lo que me refiero:
-
Antoniio
el 24/8/17Hola, me han pedido que calcule las coordenadas de los sig. vectores:
Y, teniendo en cuenta lo siguiente:
Entonces, cómo encuentro las parejas de vectores para R2 y como encuentro m2 (con el gorrito)
Gracias de antemano.
-
Gonzalo Acosta
el 24/8/17 -
Kevin Esteban
el 23/8/17Buenas tardes, alguien podria ayudarme con el desarrollo de este ejercicio la verdad me estanco en un punto y si podrian enviarme el proceso les estaria muy agradecido.
Antonius Benedictus
el 23/8/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
Ángel
el 24/8/17θ1 es sesgado, si n>2, entonces no sería buen estimador de µ (media de x1 y x2)
θ2 es insesgado (media aritmética)
θ3 es sesgado, porque cuando n tiende a infinito se le da más peso específico a los valores primero y último(un 25 por ciento siempre a cada uno) .
https://www.uv.es/ceaces/tex1t/4%20estimacion/propiedades.htm
-
Keyko Yance Chacón
el 23/8/17Hola, buen día, escribo desde Perú, quería saber si podrian darme una cuenta directa de pago, porque tengo problemas al realizar el pago mediante tarjeta , por favor . Gracias
-
Guillem De La Calle Vicente
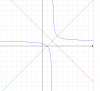
el 23/8/17Dibuje mediante un ordenador o calculadora las gráficas de las funciones dadas. Examine las gráficas (ampliándolas o reduciéndolas si es necesario) y busque las simetrías. ¿Respecto a qué rectas y/o puntos son simétricas las gráficas? Intente verificar sus conclusiones algebraicamente.
f(x)=(x-1)/(x-2)
Antonius Benedictus
el 23/8/17 -
ROSARIO
el 23/8/17Hola. Me presento. Soy estudiante de CC.Ambientales. Esta tarde he lanzado dos cuestiones en el chat pero de momento no he tenido respuesta y estoy algo perdida porque no sé si he preguntado a un profesor o a un alumno. En todo caso no he recibido respuesta. Quisiera adjuntar dos archivos en este foro pero no veo el icono de insertar. Se puede? Gracias. Saludos.
-
Manuel Perez
el 23/8/17 -
Manuel Moreno Peinado
el 23/8/17muy buenas a todos. llevo tiempo intentando resolver estos problemas y no le encuentro una solución:( necesito vuestra ayuda:
1. un comerciante quiere vender 60.000€ todos sus ordenadores. se le estropean 2 y tiene que vender otros 2 ordenadores 50€más caros para recaudar lo mismo.
¿cuantos ordenadores tenía y a qué precio?
2.las diagonales de un rombo suman 42metros con un área de 216 metros cuadrados. ¿cuál es el perimetro del rombo?
3.hay una clase con 5 chicos más que chicas, en total son más de 20 alumnos pero menos de 25. ¿cuál es la composición de la clase?
4. ¿cuantos litros de vino de 5€/litro se deben mezclar con 20 litros de otro vino de 3´50€/litro para que el precio de la mezcla sea inferior a 4€/litro?
Ángel
el 23/8/173) Chicas=x, chicos=x+5
20 < x+x+5 <25
(*) 20 < x+x+5
2x > 15
x > 15/2
(**) x+x+5 <25
2x<20
x<10
Por lo tanto, 15/2<x<10, con x∈ℤ -----------------> x1=8 , x2=9 serán el número chicas posibles
También y1=8+5= 13 , y2=9+5= 14
SE PUEDEN HACER DOS COMPOSICIONES DE LA CLASE QUE CUMPLAN NUESTRA RESTRICCIÓN ORIGINAL:
8 CHICAS Y 13 CHICOS (UNA CLASE DE 21 ALUMNOS)
9 CHICAS Y 14 CHICOS (UNA CLASE DE 23 ALUMNOS)
Antonio Silvio Palmitano
el 23/8/171)
Puedes denominar: n a la cantidad de ordenadores, y p al precio inicial de cada ordenador.
Luego plantea:
n*p = 60000 (venta inicial),
(n - 2)*(p + 50) = 60000 (venta final).
Solo queda que resuelvas el sistema de ecuaciones.
2)
Recuerda la expresión del área de un rombo: D*d/2 = A, y ten en cuenta la relación entre las diagonales en tu enunciado
por lo tanto tienes:
D*d/2 = 216,
D + d = 42.
Solo queda que resuelvas el sistema de ecuaciones.
3)
Puedes denominar: x a la cantidad de chicos e y a la cantidad de chicas, luego tienes:
x = y + 5 (1),
20 < x + y < 25,
sustituyes la expresión señalada (1) en la doble inecuación y queda:
20 < y + 5 + y < 25,
restas 5 en los tres miembros, reduces términos semejantes en el miembro central y queda:
15 < 2y < 20,
divides por 2 en los tres miembros de la doble inecuación y queda:
7,5 < y < 10,
por lo tanto, los valores de y (cantidad de chicas) pueden ser (observa que tienes dos opciones):
a)
y = 8, reemplazas en la ecuación señalada (1) y tienes: x = 13 (21 alumnos en total),
b)
y = 9, reemplazas en la ecuación señalada (1) y tienes: x = 14 (23 alumnos en total).
4)
Puedes llamar x al volumen de vino más caro (observa que el volumen de vino más barato es 20 litros),
y n al volumen total de vino.
Luego tienes las ecuaciones:
x + 20 = n (1),
y luego puedes plantear los costos:
5*x + 3,50*20 < 4*n;
luego, resuelves el segundo miembro, sustituyes la expresión señalada (1) en la inecuación, y queda:
5*x + 70 < 4*(x + 20),
distribuyes en el segundo miembro y queda:
5*x + 70 < 4x + 80,
haces pasajes de términos y queda:
x < 10.
Espero haberte ayudado.
