logo_unicoos

Foro de preguntas y respuestas de Matemáticas

logo beUnicoos
Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.
Ir a beUnicoos

  • icon

    Lorena Llanos
    el 3/5/17

    Buen día,

    Su ayuda comprobando si el desarrollo de este ejercicio es correcto


    La gráfica que me resulta es esta:



    Mil gracias

    reply•thumb_up•0 voto/s•flag
    icon

    Ángel
    el 3/5/17

    Perfecto :)

    Sólo cierra el paréntesis de casi el final  y apañao.

    thumb_up•2 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    andres
    el 3/5/17

    Hola, es posible que me puedan ayudar con este ejercicio 

    reply•thumb_up•0 voto/s•flag
    icon

    Ángel
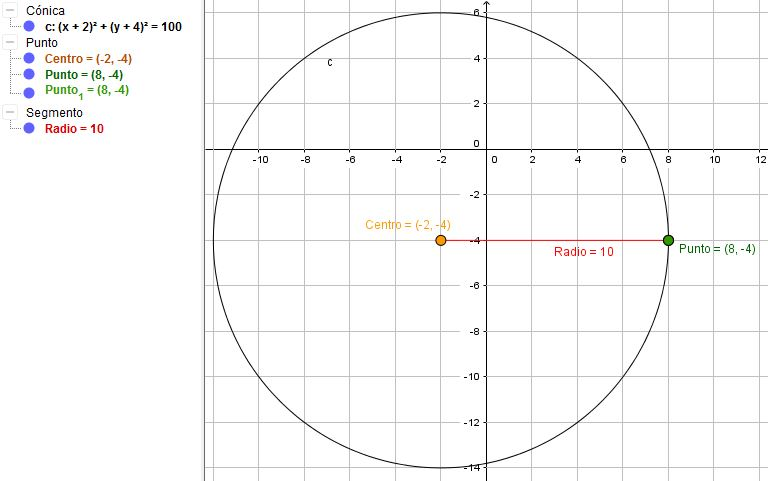
    el 3/5/17

    -Para saber si es una función de densidad tendremos que verificar estas 2 condiciones:

    1. f(x)≥0

    2. +inf∫-inf  f(x)dx=1 ----->El área total encerrada bajo la curva es igual a 1


    https://www.youtube.com/watch?v=Q6ZbpyU1OYw

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Ángel
    el 3/5/17

    En tu ejercicio se cumple de manera obvia las primera condición: 


    Pero no la segunda: Si integramos 0.05x obtenemos 0.025x2

    y para calcular el área tendremos que hacer la integral definida entre 0 y 20 (en 20 sería 0.025 (20)2=10 y en 0 sería cero....ya que 10-0=10

    no es una función de densidad, ya que su valor tendría que ser de "1"

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Javier Marquez
    el 3/5/17

    Hola , tengo una duda del tema de funciones. En general,como se determinan intervalos de crecimiento o decrecimiento en una función? sin usar derivadas

    reply•thumb_up•0 voto/s•flag
    icon

    Ángel
    el 3/5/17


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Javier Marquez
    el 3/5/17

    Entiendo la teoría, pero me refiero al momento de hacer un ejercicio donde me pidan intervalos de crecimiento o decrecimiento, existe algún método o procedimiento para encontrarlos?

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    suficiente
    icon

    Ángel
    el 3/5/17

    Por ejemplo donde haya cambio de pendiente positiva a negativa o viceversa en los puntos infinitamente cercanos a izquierda y derecha de los hipotéticos máximo o mínimo.

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Daniel Andrés
    el 3/5/17

    Buenas tengo este ejercicio, sé bien que se realiza por combinaciones , pero me confunde esa condición. Quisiera que me ayudaran con ella para ver si logro entender como realizarla 

    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 3/5/17

    Vamos por etapas, y observa que tenemos tres autos, con once lugares en total para ser ocupados por nueve personas.:

    1°) Elegimos los conductores:

    N1 = C(9,3) = 9!/(3!*6!) = 84 posibilidades.

    2°) Elegimos los lugares que serán ocupados por las personas restantes, y observa que tenemos ocho lugares para asignar uno a cada una de las seis personas que faltan ubicar:

    N2 = C(8,6) = 8!/(2!*6!) = 28 posibilidades.

    3°) Por el principio de multiplicación, tienes que la cantidad total de posibilidades queda:

    N = N1*N2 = 84*28 = 2352.

    Luego, contamos las posibilidades para que el carro más grande quede con dos lugares vacíos:

    a) Elegimos la persona que completará la capacidad del auto más pequeño:

    n1 = C(6,1) = 6!/(1!*5!) = 6 posibilidades.

    b) Elegimos las tres personas que completarán la capacidad del auto mediano:

    n2 = C(5,3) = 5!/(2!*3!) = 10 posibilidades.

    c) Ubicamos a las dos personas que faltan ubicar en el auto más grande:

    n3 = 1 posibilidad.

    Luego, por el principio de multiplicación, tenemos que la cantidad de posibilidades de tener dos lugares vacíos en el auto más grande queda:

    n = n1*n2*n3 = 6*10*1 = 60 posibilidades.

    Luego, la probabilidad de tener que los dos lugares libres queden en el auto más grande queda:

    p = n/N = 60/2352 = 5/196.

    Espero haberte ayudado.



    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Daniel Andrés
    el 3/5/17

    Excelente muchas gracias !


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?

  • Usuario eliminado
    el 3/5/17

    Hola. ¿pueden ayudarme a demostrar está formula de integración? usando el teorema de pitágoras.
    Lo he intentado pero no me sale.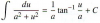

    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 3/5/17


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    suficiente
    icon

    Antonio Silvio Palmitano
    el 3/5/17

    Puedes aplicar la sustitución (cambio de variable):

    u = a*tanw,de donde tienes:

    du = a*(1/cos2w)*dw = a*dw/cos2w, y también tienes:

    a2 + u2 = a2 + a2*tan2w = a2*(1 + tan2w) = a2*(1/cos2w) = a2/cos2w, y también tienes:

    u/a = tanw, que al componer en ambos miembros con la función inversa de la tangente queda:

    arctan(u/a) = tan-1(u/a) = w.

    Luego, pasamos a la resolución de la integral:

    I = ∫ du/(a2 + u2), sustituyes las dos primeras expresiones remarcadas y queda:

    I = ∫ (a*dw/cos2w)/(a2/cos2w), simplificas, extraes el factor constante y queda:

    I = (1/a) * ∫ dw, integras y queda:

    I = (1/a)*w + C, sustituyes la última expresión remarcada y queda:

    I = (1/a)*tan-1(u/a) + C.

    Espero haberte ayudado.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    suficiente
  • icon

    Jonathan Yañez
    el 3/5/17

    --------------------TRIGONOMETRÍA------------------
    cos(π-x)sen(π-x) +sen(2x) = -sen(2π+x)

    Respuesta:

    x = πk

    x = 2πk + π

    Necesito saber si las mis respuestas están bien y si son las únicas o me falto alguna.


    MI RESOLUCIÓN:

    cos(π-x)sen(π-x) + sen(2x) = -sen(2π+x)

    -cos(x)sen(x) + 2senxcosx = -sen(x)

    sen(x)cos(x) = -sen(x)

    sen(x)cos(x)+sen(x)=0

    sen(x) (cos(x)+1)=0

    1.-sen(x)=0 ------> (π) y(2π)-->(π)k

    2.-cos(x)+1=0--> cos(x)=-1-->180°-->(π)+(2π)k




    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 3/5/17

    Tienes las identidades:

    cos(π-x) = cosπ*cosx + senπ*senx = -1*cosx + 0*senx = - cosx + 0 = - cosx;

    sen(π-x) = senπ*cosx - cosπ*senx = 0*cosx - (-1)*senx = 0 + senx = senx;

    sen(2x) = 2*senx*cosx;

    sen(2π+x) = sen(2π)*cosx + cos(2π)*senx = 0*cosx + 1*senx = 0 + senx = senx.

    Luego, planteas la ecuación del enunciado:

    cos(π-x)*sen(π-x) + sen(2x) = - sen(2π+x), sustituyes las cuatro expresiones de las identidades y queda:

    - cosx*senx + 2*senx*cosx = - senx, reduces términos semejantes en el primer miembro y queda:

    senx*cosx = - senx, haces pasaje de término y queda:

    senx*cosx + senx = 0, extraes factor común y queda:

    senx*(cosx + 1) = 0, y por anulación de un producto tienes dos opciones:

    1)

    senx = 0, luego compones con la función inversa del seno en ambos miembrosy queda:

    x = 0 + k*π, con k ∈ Z;

    2)

    cosx + 1 = 0, haces pasaje de término y queda:

    cosx = - 1, luego compones con la función inversa del coseno en ambos miembros y queda:

    x = π + 2*m*π, con m ∈ Z.

    Espero haberte ayudado.

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Jonathan Yañez
    el 3/5/17

    Muchas gracias!!! Como siempre la mejor respuesta, ojala mis profesores fueran igual de claros para explicar y resolver los problemas.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    Emi
    el 3/5/17

    Hola! Necesito ayuda con un ejercicio de inducción. Mi problema viene a la hora de valerme de la hipótesis inductiva para demostrar p(k+1). El enunciado dice: Probar que para todo n perteneciente a N(los naturales) se tiene

     

    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 3/5/17


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    luisa charry
    el 3/5/17

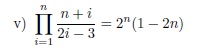
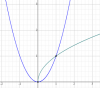
    Hola....si me podrían ayudar con este ejercicio.

    y=x^2

    y^2=x

    Es de área entre curvas.

    reply•thumb_up•0 voto/s•flag
    icon

    Ángel
    el 3/5/17

    Tienes las funciones:

    y=x2

    y2=x ----> y=√x


    Das valores a equis dentro del dominio y obtienes la tabla de valores, los representas en la gráfica y obtienes: 


    Tanto gráficamente como igualando las funciones puedes comprobar que el área encerrada entre las curvas está entre x=0 y x=1

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    Marcos
    el 3/5/17


    Hola.. una duda

    esta correcto esto? 

    solo con compuertas nand

    reply•thumb_up•0 voto/s•flag
  • icon

    Valeria
    el 3/5/17

    Aca van los ultimos, gracias por todo.otro

    reply•thumb_up•0 voto/s•flag
    icon

    Axel Morales Piñón.
    el 3/5/17


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Axel Morales Piñón.
    el 3/5/17


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo