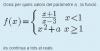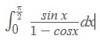-
Jose Maria Pelaez Rodriguez
el 16/4/17Buenas Tardes estoy en 1 de la ESO podriais ayudarme con problemas de ecuaciones , las ecuaciones gracias a los videos las he captado rapidamente pero los problemas....hay algun video ?
Ángel
el 16/4/17
Antonius Benedictus
el 16/4/17No te fijes en 1º de Bachiller. Son problemas de ESO.
-
Luciano Serra
el 16/4/17Hola!, me piden hallar la inversa de f(x) = ln (x2 + 4) , x > 0 y resuelvo así: y = ln (x2 + 4) ----> (intercambio "y" y "x") tal que x = ln (y2 + 4) ---> por lo tanto e x = (y2 + 4) -----> ex - 4 = y2 ----> y = √(e x - 22) , pero cuando sustiuyo para corroborar no me devuelven los mismos valores. Muchas gracias!
-
Usuario eliminado
el 16/4/17 -
David Avalos Fernàndez
el 16/4/17 -
David Avalos Fernàndez
el 16/4/17 -
Usuario eliminado
el 16/4/17
corrección por favor y un pregunta, ¿no es necesario hacer la operación no? -
Marta
el 16/4/17 -
emerson acosta
el 16/4/17Buenos dias! me podrian ayudar con esta integral? me da una indeterminación 0/0 y no se donde debo aplicar la regla de bernoulli (lhopital). si dentro de la integral o resolver la integral de manera infinida luego a ese resultado aplicarle la regla.
Antonio Silvio Palmitano
el 16/4/17Observa que la integral es impropia, ya que el denominador se anula para x = 0, que es el límite inferior de integración.
Luego, planteamos el problema en tres pasos:
1°) Resolvemos la integral indefinida, para ello puedes plantear la sustitución (cambio de variable):
w = 1 - cosx, de donde tienes: dw = senx*dx, luego sustituyes y la integral queda.
I = ∫ (1/w)*dw = ln|w| + C = sustituyes y queda = ln|1 - cosx| + C.
2°) Evaluamos para el intervalo: a ≤ x ≤ π/2 (donde a es un valor genérico) y queda:
I = ln|1 - cos(π/2)| - ln|1 - cosa| = ln|1 - 0| - ln|1 - cosa| = ln(1) - ln|1 - cosa| = 0 - ln|1 - cosa| = - ln|1 - cosa|.
3°) Planteamos el límite de la expresión anterior para a tendiendo a cero por la derecha y queda:
I = Lím(a→0+) ( - ln|1 - cosa| ) = +∞,
ya que tienes que el argumento del logaritmo tiende a cero, lo que lleva a que el logaritmo tienda a - infinito, y que la integral tienda a + infinito.
Por lo tanto, concluimos que la integral impropia del enunciado es divergente.
Espero haberte ayudado.
-
Blánca Rubí Aréllanó Uribe Ö
el 16/4/17Hola buenos dias alguien que pudiera ayudarme con esta pregunta, si fuera tan amable, de antemano muchas gracias.
Describe el significado geométrico (en términos de distancias), tanto de la media como de la desviación estándar.
