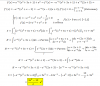-
Buenas noches.Como se resuelve este tipo de ejercicios? Con las integrales definidas estoy bien, pero con las aplicaciones estoy muy flojo.


Antonio Silvio Palmitano
el 26/11/16Puedes plantear la ecuación cartesiana explícita de la recta que pasa por los puntos de coordenadas (2,0) y (0,4), lo haces y queda:
y = - 2x + 4, luego despejas x y queda:
x = (4 - y)/2 = g(y), y observa que tienes que y pertenece al intervalo [0,4].
Luego, planteamos para el volumen de revolución alrededor del eje coordenado OY:
Vy = π ∫ ( g(y) )2 dy = π ∫ ( (4 - y)/2 )2 dy = (1/4) π ∫ (16 - 8y + y2) dy = (1/4) π [ 16y - 4y2 + y3/3 ], evaluamos entre 0 y 4 y queda:
Vy = (1/4) π (64 - 64 + 64/3) = (16/3)π.
Espero haberte ayudado.
-
He visto sus videos en Youtube pero no se como relacionarlo con este problema. por favor me podrían ayudar?
-


David
el 29/11/16Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Hola, necesito ayuda con el siguiente ejercicio de funciones:
1) Demuestre que la función f(x)= x^2 - 2 tiene al menos una raíz real en el intervalo [1,2]
Por teorema de Bolzano me dió: f(1)= -1 < 0 y f(2)= 2 > 0 por tanto existe un c para f(x) que en el intervalo [1,2] es igual a 0
Es correcto? que otra estrategia me sirve para demostrar que existe dicha raíz? gracias.
-
Hola, me pueden ayudar con el siguiente ejercicio de límites? empieza con la gráfica de una función y me piden determinar si existen los siguientes límites:
a) lim cuando x tiende a -6 solo por la derecha
b) lim cuando x tiende a -3
Debo empezar calculando los límites laterales según lo indicado en la gráfica? no me dan la función, solo esa gráfica.
Hasta ahora he puesto:
a) No existe ya que cuando nos acercamos por la derecha tiende a -1 y cuando nos acercamos por la izquierda tiende a 0 (o acaso no está definido? tengo dudas en este punto)
b) Existe y es 2
Están correctos? tengo especial duda en -6 cuando nos acercamos por la izquierda.


Antonio Silvio Palmitano
el 26/11/16Observa que en el inciso a) te piden calcular el límite de la función para x tendiendo a - 6 por la derecha, y es igual a -1 tal como has dicho (no es necesario discutir más).
En el inciso b) tu respuesta es correcta, y puedes justificarla diciendo que los dos límites laterales existen (aquí si es preciso discutir los dos límites laterales) y son iguales a 2, por lo que el límite existe y es igual a 2 tal como has dicho.
Espero haberte ayudado.
-
Buenas tardes.Los molesto con este ejercicio de area entre curvas.No entiendo como plantear la sumatoria de integrales que calculen el area sombrada..Las integrales definidas las se resolver, lo que no capto es el planteo del area.


Antonio Silvio Palmitano
el 26/11/16Observa que puedes plantear tres subintervalos: I1 = (-3,-2), I2 = (-2,1) y I3 = (1,3).
Observa que en cada uno de ellos tienes una gráfica "más alta" (A), y otra "más baja" (B).
Luego, para cada intervalo, plantearemos una integral de la forma: ∫ ( A(x) - B(x) )dx, y luego sumaremos los tres resultados.
1) Para el primer subintervalo:
A(x) = 3 - x, B(x) = x2 - 9, y luego tenemos: A(x) - B(x) = (3 - x) - (x2 - 9) = 12 - x - x2,
luego queda para que calcules la intergral correspondiente.
2) Para el segundo subintervalo:
A(x) = x2 + 1, B(x) = x2 - 9, y luego tenemos: A(x) - B(x) = (x2 + 1) - (x2 - 9) = 10,
luego queda para que calcules la integral correspondiente.
3) Para el tercer subintervalo:
A(x) = 3 - x, B(x) = x2 - 9, y luego tenemos: A(x) - B(x) = (3 - x) - (x2 - 9) = 12 - x - x2,
luego queda para que calcules la integral correspondiente.
Espero haberte ayudado.
-

Buenas tardes profe. Necesito su ayudaa!!...
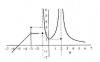
Quisiera me ayude con el ejercicio 49; sobre todo que me ayude en el análisis de la función exponencial, ya que no es tan fácil de graficar. POR FAVOR....
GRACIAS Y MUCHAS MÁS GRACIAS PROFEE!!.


Antonio Silvio Palmitano
el 25/11/16Observa la expresión de la derivada primera de la función:
y ' = - e-x(x2+3x+1) + e-x(2x+3) = e-x(-x2 -3x-1+2x+3) = e-x(-x2-x+2) = - e-x(x2 + x - 2).
Luego planteamos la condición de punto crítico:
y ' = 0, sustituimos y queda la ecuación:
- e-x(x2 + x - 2) = 0, hacemos pasaje de factor como divisor (recuerda que el factor exponencial es distinto de cero), resolvemos el segundo miembro y queda:
x2 + x - 2 = 0, cuyas soluciones son:
x = -2, x = 1.
Luego, queda para que continúes la tarea.
Espero haberte ayudado.