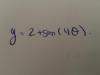Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Jon Aginaga
el 13/11/16

Buenas, ¿podríais decirme en qué punto me he equivocado por favor? No soy capaz de encontrar el error. Muchas gracias.

••0 voto/s
•
Antonio Silvio Palmitano
el 13/11/16
Tienes que tomar precauciones cuando multiplicas por una matriz.
Observa que tienes la ecuación matricial:
AX - BCX = A, extraes factor común derecho en el primer miembro y queda:
(A - BC)X = A, si la matriz (A - BC) es invertible, multiplicas a izquierda por su inversa en ambos miembros y queda:
(A - BC)^-1(A - BC)X = (A - BC)^-1A, resolvemos los dos primeros factores en el primer miembro y queda:
IX = (A - BC)^-1A, resolvemos el primer miembro y llegamos a:
X = (A - BC)^-1A.
Espero haberte ayudado.

•0 voto/s
•

Cancelar
ayelen daisi
el 13/11/16

Hola, estuve intentando resolver este enunciado y se me hace imposible, me ayudaría por favor, gracias.

••0 voto/s
•
Antonio Silvio Palmitano
el 13/11/16
Observa que tienes la abscisa del punto de tangencia: x_o = 2, y que la ordenada la puedes calcular: y_o = g(2) = (3*2² + 2 +2)/√(2+2) = 16/2 = 8,
por lo que las coordenadas del punto de tangencia son: P_o(2,8).
Luego, observa que la expresión de la función es un cociente de la forma: g(x) = u/v, cuya derivada tiene la forma: g ' (x) = ( u ' * v - u * v ' ) / v² (*), y tenemos:
u = 3x2 + x + 2, cuya derivada queda: u ' = 6x + 1
v = √(x+2), cuya derivada queda: v ' = 1 / 2√(x+2).
Luego evaluamos las cuatro expresiones anteriores para x_o = 2 y quedan:
u(2) = 16, luego: u ' (2) = 13,
v(2) = 2, luego: v ' (2) = 1/4.
Luego, reemplazamos en la expresión señalada (*) y planteamos para la pendiente de la recta tangente buscada:
m = g ' (2) = ( 13*2 - 16*1/4 )/4 = 22/4 = 11/2.
Por último, planteamos la ecuación cartesiana de la recta tangente buscada:
y - y_o = m(x - x_o), reemplazamos valores y queda:
y - 8 = (11/2)(x - 2), distribuimos, hacemos pasaje de término, reducimos términos semejantes y llegamos a:
y = (11/2)x - 3, que es la ecuación cartesiana explícita de la recta tangente pedida.
Espero haberte ayudado.

•1 voto/s
•
César
el 13/11/16
Recta tangente y normal

•1 voto/s
•
ayelen daisi
el 13/11/16
Muchas gracias.

•0 voto/s
•

Cancelar
Carlos Ojeda
el 13/11/16

Hola. pido ayuda con una pequeña duda que me tiene bloqueado, en la parte final de la solución de esta integral, en el denominador,¿por qué dividen entre 2 (x-2)^2 y el 4 se convierte en 1,luego en el numerador,¿por qué ponen 1/2 multiplicando?¿qué cambio se hace para que el 16/3 se convierta en 1/2?¿y el 4 que está multiplicando fuera? sé que son cambios que se hacen para adaptar la expresión a la fórmula de la integral de la arcotangente, pero no sé qué pasos se siguen. Si me podrían explicar pasito a pasito esos cambios. Gracias

••0 voto/s
•
César
el 13/11/16
Por buscar el arctg como primitiva

•1 voto/s
•

Cancelar
LEO LACH
el 13/11/16

Hola, tengo duda en este problema de distribución de probabilidad de variable discreta, donde dice " ... duran mas de 1000 horas " y "duran al cabo de 1000 horas ", son lo mismo entonces la variable aleatoria X = nº de bombillas que duran mas de 1000 horas,luego se aplicaría la dist. binomial para resolver la pregunta P(X>=5) = Sumatoria de x=5 hasta 10, (combinatoria de (10,x))*(0.25^x)*(0.75^(10-x)),al final me sale 0.078126, ayuda pls.

••0 voto/s
•
Antonio Silvio Palmitano
el 13/11/16
Has planteado bien. Tratas con una distribución binomial, con n = 10, p = 0,25, q = 1 - p = 0,75, y piden calcular p(X ≥ 5) = ∑(k=5,10) ( C(10,k) * 0,25^k* 0,75^{^10-k} ).
Luego, si dispones de una tabla para esta distribución puedes obtener un resultado muy bien aproximado, y en caso contrario, deberás resolver los seis términos de la sumatoria.
Espero haberte ayudado.

•1 voto/s
•

Cancelar
Magalí
el 13/11/16

Por favor !necesito ayuda para terminar ésta integral :(

••0 voto/s
•
Hugo
el 13/11/16
haz la sustitucion, u ≡ x²+3x+2 , si te fijas lo de arriba es la derivada de lo que esta dentro de la raiz

•1 voto/s
•
Antonio Silvio Palmitano
el 13/11/16
Has hecho correctamente la sustitución, y has planteado, como sugiere el colega Hugo, la sustitución:
t = x²+3x+2, cuyo diferencial queda: dt = (2x+3)dt.
Observa que los límites de integración para la variable x son x₁ = -2 y x₂ = 0, pero para la nueva variable t, sus límites son:
t₁ = (-2)² + 3(-2) + 2 = 0, y t₂ = 0² + 3*0 + 2 = 2.
Luego has aplicado bien la sustitución (solo te faltó cambiar los límites de integración), y la integral te quedó (indicamos con corchetes que debemos evaluar con Regla de Barrow):
I = ∫ ( t^-1/2 )dt = [ 2t^1/2 ] = [ 2√(t) ], evaluamos entre 0 y 2 y queda:
I = 2√(2) - 2√(0) = 2√(2) - 0 = 2√(2).
Espero haberte ayudado.

•1 voto/s
•

Cancelar
pau
el 13/11/16

Hola! En esta ecuacion y-x=1 2^x+2 ^y =12
despejo x de la 1º ecuacion y me queda 2^x +2^x+1=12
y ya no se que hacer. Ayuda!!!

••0 voto/s
•
Gabriel
el 13/11/16
Hola pau, aquí te viene la ayuda.
2^x+2^x+1=2^x+2^x·2¹=2^x(1+2)=3·2^x=12
2^x=12/3=4=2²
Por lo que, siendo las bases iguales x=2

•0 voto/s
•

Cancelar
Felipe Rojido
el 13/11/16

Hola, me podrían ayudar con el siguiente problema? lo he intentado pero no lo entiendo.
El problema dice;
Suponga una población cuyo modelo de crecimiento está dado por P(t) = 4e^{0,02 t}millones a partir del año 2000. ¿Cuándo la población tendrá 5 millones de habitantes?

••0 voto/s
•
David
el 13/11/16
4e0,02 t =5 ....e0,02 t =(5/4) Es una ecuacion exponencial... Ecuaciones exponenciales y logaritmicas
Aplicando logaritmos neperianos a ambos lados de la ecuacion ln e0,02 t =ln(1,2) .... 0,02.t= ln(1,2)... t=ln(1,2)/ 0,02...

•1 voto/s
•

Cancelar
Joel Perez
el 13/11/16

Amigos buenos dias, necesito la respuesta a estos límites

••0 voto/s
•
David
el 13/11/16
Lo siento pero no se trata de que os hagamos los deberes de 5 en 5. y menos si son como estos, universitarios y de cierto nivel. Ten en cuenta que ni siquiera solemos responder dudas universitarias pues unicoos por ahora se queda en bachiller. cuando hacemos alguna excepción es porque la duda es muy concreta y "fácil" de resolver. Espero lo entiendas. Un abrazo!

•0 voto/s
•

Cancelar
Carlos Ojeda
el 13/11/16

Hola, ¿podrían hacer este ejercicio de continuidad? a me dio 2 y b me dio 2 también, pero no estoy seguro de mi resultado. Gracias

••0 voto/s
•
Gabriel
el 13/11/16
¿Qué dice exactamente el enunciado? ¿te pide la continuidad?
Si fuera así, estaría bien, a mí también me dan los valores de a y b con solución 2.
Saludos.

•1 voto/s
•
Carlos Ojeda
el 13/11/16
Pide hallar los valores de a y b para que la f(x) sea derivable en todo R.

•0 voto/s
•
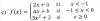
Gabriel
el 14/11/16
Vale, dicho eso, hay que decir que es continua pero no derivable.
Cuando se calcula la derivada de f(x), tenemos que
(1) 2, para x<-1
(2) a, para -1<x<0
(3)6x, para x>0
Así, igualando (1) y (2) para x=-1, nos da a = 2,
e igualando (2) y (3) para x=0, nos da a = 0, por lo que NO ES DERIVABLE.
Espero que te haya sido útil.

•0 voto/s
•
Ángel
el 14/11/16
Si a=2 y b=2
*Será contínua en R
*Será derivable en R -{0} (todo el conjunto de los números reales, excepto el cero)

•1 voto/s
•

Cancelar
Jose Manuel
el 13/11/16

Vereis tengo que representar lo siguiente de la foto,como podia expresarlo sin que sea un angulo 4 es decir para poder operar con los angulos fundamentales ,me explico poder transformqr sen(4alfa) a lo siguiente x por el seno de alfa ,alguien me ayuda es para representarlo

••0 voto/s
•
David
el 13/11/16
sen(4x)=sen(2.2x)= 2.sen(2x).cos(2x) = 2.(2senx.cosx.(cos²x-sen²x).. ¿mejor?

•1 voto/s
•
Jose Manuel
el 13/11/16
muchisimas gracias david eso era justo lo que necesitaba eres un crack

•0 voto/s
•

Cancelar