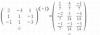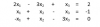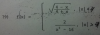-
Hoola! En este ejercicio de números complejos, ¿cómo saco las raíces si no puedo hallar los ángulos? Gracias


Nicolas Tenorio Perez
el 1/11/16No me acuerdo muy bien, pero cuando eran números complejos, yo usaba arc tg, usa el arc tg reemplazando los valores de tu ecuación en el arc tg. Recuerda que la ordenada es dividida entre la abscisa y creo que las ordenadas eran los imaginarios y las abscisa los reales, por ejemplo, Z = 1+2i, entonce el ángulo es arc tg (2/1).


Antonio Silvio Palmitano
el 1/11/16Observa que te ha quedado la ecuación: z³ = 1+i, y observa también que el número complejo 1+i está representado por el punto del primer cuadrante cuyas coordenadas son (1,1).
Luego expresamos al número complejo en forma polar (módulo)(argumento):
módulo: |1+i| = V(1² + 1²) = V(1+1) = 2,
argumento: tanθ = 1/1 = 1, de donde tienes: θ = arctan(1) = 45° = π/4,
con lo que tenemos: 1+i = ( V(2) )(45°).
Luego la ecuación queda:
z³ = ( V(2) )(45°), luego hacemos pasaje de potenicia como raíz y queda:
z = ³√( V(2) )(45°), luego aplicamos la fórmula de De Moivre para las raíces:
z = ( ³√(V(2)) )( (45° + 360°*k)/3 ), con k = 0,1,2,
luego resolvemos en el módulo (escribimos raíz sexta con (6V)), distribuimos el denominador en el argumento y queda:
z = ( (6V)(2) )(15° + 120°*k), con k = 0,1,2,
luego tenemos las tres raíces (que expresamos también en forma trigonométrica):
z0 = ( (6V)(2) )(15°) = ( (6V)(2) )(cos15° + i*sen15°)
z1 = ( (6V)(2) )(135°) = ( (6V)(2) )(cos135° + i*sen135°)
z2 = ( (6V)(2) )(255°) = ( (6V)(2) )(cos255° + i*sen255°).
Espero haberte ayudado.
-
Hola, usando la fórmula de Moivre,¿cómo se halla el ángulo para el cálculo de la potencia cuando tenemos por ejemplo: (1 - √3 i)^3? Es que he visto que restan 2pi y no entiendo mucho. Gracias


Antonio Silvio Palmitano
el 1/11/16Debes establecer primero en cuál de los cuadrantes se encuentra el punto que representa al número complejo:
si pertenece al primero, el argumento que obtienes con tu calculadora es directamente el argumento del número complejo,
si pertenece al segundo, al argumento que obtienes con tu calculadora le debes sumar π,
si pertenece al tercero, al argumento que obtienes con tu calculadora le debes sumar π,
si pertenece al cuarto, al argumento que obtienes con tu calculadora le debes sumar 2π.
Observa que en tu ejercicio, la base de la potencia es el número complejo: 1 - V(3)i, que está representado por el punto de coordenadas (1,-V(3)) que pertenece al cuarto cuadrante, luego tienes:
módulo: |1 - V(3)i| = V( 1 + 3) = V(4) = 2,
argumento: tanθ = -V(3)/1= -V(3), luego: θ = arctan(V(3)) = - π/3 + 2π = 5π/3.
y el número complejo expresado en forma polar queda:
1 + V(3)i = (2)(5π/3);
Luego pasamos a la potencia:
( 1 + V(3)i )³ = (2)(5π/3) )³ = aplicamos la fórmula de De Moivre para las potencias:
= ( 2³ )( 3*(5π/3 ) = resolvemos el módulo y el argumento:
= ( 8 )( 5π ) = restamos dos giros en el argumento:
= ( 8 )( 5π - 4π ) = resolvemos el argumento:
= ( 8 )(π) = expresamos en forma trigonométrica:
= 8(cosπ + i*senπ) = distribuimos y expresamos en forma binómica:
= - 8 + 0i = -8.
Espero haberte ayudado.
Luego pasamos al cálculo de la potencia
-
Hola, buenas tardes. Cómo puedo resolver un SEL usando el método de Gauss-Jordan?, ya tengo la matriz inversa:
y debo resolver, con esa matriz inversa diversos SEL pero ocupo que me ayuden con uno para poder hacer el resto por favor, este:
Espero puedan apoyarme, saludos !!
Y el resultado


Aleking
el 3/11/16Lo que pasa es que no tiene sentido usar la matriz inversa y Gauss-Jordan simultáneamente, porque no obtienes lo que te piden (estarías resolviendo otro SEL distinto).
Como yo lo veo, o bien usas Gauss-Jordan y estaría perfecto como tú lo hiciste al principio, o bien usas la matriz inversa y lo haces como yo te indiqué (que es mucho más rápido y simple). Me extraña mucho que te dijeran que usaras las dos cosas a la vez. ¿Podrías enseñarme el enunciado original, por favor?


Aleking
el 3/11/16Ahora está más claro. El ejercicio consta de dos pasos:
1º) Usar Gauss-Jordan para encontrar la matriz inversa (imagino que ya la calculaste porque la dabas en el primer enunciado).
2º) Usar la matriz inversa para resolver el sistema. Aquí tienes que hacer lo que te dije en mi primera respuesta, es decir, multiplicar la matriz inversa obtenida por (2 -1 0). Lo que marqué en amarillo.
-
Aca va de nuevo:
Considere las siguientes funciones: f, g, h: [0.a]→R
El valor de (alfha) ∈ R de modo que: Area 1= Area 2, es:........


Antonio Silvio Palmitano
el 1/11/16Va una orientación:
para plantear el área de la región señalada (1) puedes plantear integración de g(x) - f(x) con respecto a x, con x entre 0 y a;
pero observa que
para plantear el área de la región señalada (2) puedes plantear integración pero con respecto a y, con y entre 0 y 2a² (según se aprecia en tu dibujo) por lo que debes expresar x en función de y para las funciones: y = h(x) e y = g(x), para luego integrar.
Haz el intento, y si es necesario puedes volver a consultar.
Espero haberte ayudado.
-
Buenas noches gente, les queria pedir un favor, si alguien sabe como resolver este ejercicio por el metodo de Definicion de Integral de Linea, llegue al resultado de (-12pi) pero no estoy seguro, si alguien lo hiciera y me dijera si el resultado es correcto serie de gran ayuda, desde ya muchas gracias.



Antonio Silvio Palmitano
el 1/11/16Tenemos la curva C, que es intersección entre las superficies:
S1: z = 2x² + 2y²
S2: z = 4y, igualamos y queda la ecuación:
2x² + 2y² = 4y, dividimos en todos los términos de la ecuación por 2, hacemos pasaje de término y queda:
x² + y² - 2y = 0, luego completamos un binomio elevado al cuadrado para y:
x² + (y - 1)² = 1, observa que tienes (en R^2) la ecuación de una circunferencia con centro (0,1) y radio 1, por lo que podemos parametrizar:
x = cost, y = sent + 1, z = 4(sent + 1), que corresponde la función vectorial de posición:
r(t) = < cost , sent + 1 , 4sent + 4 >, con 0 ≤ t ≤ 2π.
Luego derivamos y obtenemos la función vectorial:
r ' (t) = < -sent , cost , 4cost >.
Luego, el campo vectorial cuya expresión es F = < 2z , x² - y , y² - x >, queda expresado en función de la variable de parametrización:
F(r(t)) = < 8sent +8 , cos²t - sent - 1 , (sent + 1)² - cost >, luego planteamos el producto escalar (lo indicamos con •) entre F y r ' (t):
F(r(t))•r ' (t) = < 8sent +8 , cos²t - sent - 1 , (sent + 1)² - cost > • < -sent , cost , 4cost > = desarrollamos y queda:
= (8sent + 8)(-sent) + (cos²t - sent - 1)cost + ((sent + 1)² - cost)4cost = distribuimos y queda:
= - 8sen²t - 8sent + cos³t - sentcost - cost + 4cost(sen²t + 2sent + 1 - cost ).
Luego, planteamos la integral de línea del campo vectorial:
I = ∫ F•dr = ∫ F(r(t))•r ' (t) dt =
= ∫( - 8sen²t - 8sent + cos³t - sentcost - cost + 4cost(sen²t + 2sent + 1 - cost )dt = queda para que desarrolles la expresión de la función y resuelvas término a término, con intervalo de integración entre 0 y 2π.
Espero haberte ayudado.
-
Hola! Alguien sabe como es la expresión del resto del siguiente polinomio?
f(X)= 3/(2-3x) de orden 4 con x0=1/3
En realidad, no sé como expresar el resto en ningún polinomio.
Saludos!


Antonio Silvio Palmitano
el 1/11/16Tienes el centro de desarrollo: xo = 1/3, y la expresión de la función, de la que planteamos las expresiones de sus derivadas hasta el orden cinco:
f(x) = 3/(2-3x), de la que calculamos: f(1/3) = 3
f ' (x)= 9/(2-3x)^2, de la que calculamos: f ' (1/3) = 9
f ' ' (x) = 54/(2-3x)^3, de la que calculamos: f ' ' (1/3) = 54
f ' ' ' (x) = 486/(2-3x)^4, de la que calculamos: f ' ' ' (1/3) = 486
f ' ' ' ' (x) = 5832/(2-3x)^5, de la que calculamos. f ' ' ' '(1/3) = 5832
f ' ' ' ' ' (x) = 87480/(2-3x)^6, de la que calculamos: f ' ' ' ' '(c) = 87480/(2-3c)^6, con c comprendido entre 1/3 y x.
Luego, el polinomio de Taylor de orden 4 de la función, con centro de desarrollo xo = 1/3 queda:
P4(x) = 3 + 9(x-1/3) + 54/2! * (x-1/3)^2 + 486/3! * (x-1/3)^3 + 5832/4! * (x-1/3)^4, resolvemos los coeficientes en cada término y queda:
P4(x) = 3 + 9(x-1/3) + 27(x-1/3)^2 + 81(x-1/3)^3 + 243(x-1/3)^4
Luego, la expresión del resto queda:
R(x) = 87480 / (5! * (2-3c)^6 ) * (x-1/3)^5 = 729/(2-3c)^6 * (x-1/3)^6.
con c perteneciente al intervalo (x,1/3), si x < 1/3, o
con c perteneciente al intervalo (1/3,x), si x > 1/3.
Espero haberte ayudado.
-
Hola, ¿por qué en este ejercicio de números complejos se multiplica denominador y numerador por "i"? Gracias



Antonio Silvio Palmitano
el 1/11/16Has resuelto correctamente el ejercicio, solo considera expresar el resultado en la forma usual (parte real + parte imaginaria multiplicada por i): 6 + (5/2)i.
Observa que el denominador es un complejo imaginario puro, por lo que puedes multiplicar por i, o por -i si prefieres, en el numerador y en el denominador para resolverlo. Pero si en el denominador tienes un número complejo propiamente dicho (con parte real no nula y parte imaginaria no nula), entonces debes multiplicar al numerador y en el denominador por el conjugado del denominador.
Espero haberte ayudado.
-
¿Alguien sabe cómo puedo resolver esto?
A partir del semestre anterior, por cuestiones de trabajo y estudio no ha podido hacer ejercicio, por lo que el aumento de su peso en kilos fue de f(x)= 0.002x+0.4 (x indica el tiempo en semestres).
a. Identifica los elementos del problema.
b. ¿Cuál es la función del aumento de peso total que ha tenido?