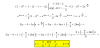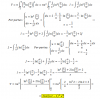No me refiero a cos3x sino a coseno al cubo de x : cos^3(x)

¿¿La formula de Moivre para simplificar cos³x??? No tiene sentido...
La formula de Moivre es para expresar números complejos, no para simplificar expresiones trigonométricas...

No son funciones.... Siento no poder ayudarte....  Unicoos por ahora se queda en bachiller...

Sólo debes aplicar la propiedad de los log cuando estos se suman o restan 

Log28 + log15 - log6 = log(28*15)/6

Log70 = log7*10

log7 + log10

0,8451+1 = 1,8451

Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. Lo siento de corazón… Espero lo entiendas

Te ayudamos un poco, Sandra: 

La identidad trigonométrica del ÁNGULO DOBLE es: sen2x = 2senx.cosx     

x=5

Alguien me podria explicar como se resuelve este ejercicio?no se ni como empezarlo ,estoy perdido

Te lo explicamos, Pablo:

El primero, Dan:

a) Comencemos por despejar en la segunda ecuación (trabajamos con valores de x e y comprendidos entre 0 y 2π), componiendo con la función inversa del seno:

x + y =  π/2, luego despejamos y queda:

y = π/2 - x (*), luego sustituimos en la primera ecuación y queda:

3x + π/2 - x = 5π/6, reducimos términos semejantes a la izquierda, hacemos pasaje de término, reducimos términos semejantes a la derecha y queda:

2x = π/3, hacemos pasaje de factor como divisor, resolvemos a la derecha y queda:

x = π/6, luego reemplazamos en la ecuación señalada (*) y queda:

y = π/2 - π/6, resolvemos y llegamos a:

y = π/3, 

por lo que concluimos que en el intervalo [0,2π] la solución es: x = π/6, y = π/3.

b) Observa que en la primera ecuación debe cumplirse que sus factores tengan igual signo, porque el producto es igual a un número positivo, y lo mismo ocurre con la segunda ecuación, por lo que tenemos que:

1) x e y pertenecen ambos al primer cuadrante,

2) x e y pertenecen ambos al tercer cuadrante.

Luego, podemos dividir miembro a miembro (observa que todos los factores a la izquierda en ambas ecuaciones deben ser distintos de cero) y queda la ecuación:

senx* cosy / cosx*seny = 1, expresamos como producto de expresiones fraccionarias a la izquierda:

senx/cosx * cosy/seny = 1, sustituimos, con las identidades trigonométricas para tangente y cotangente:

tanx * cotgy = 1, hacemos pasaje de factor como divisor:

tanx = 1/cotgy, sustituimos a la derecha (recuerda que 1/cotgy = tany):

tanx = tany, luego, tenemos opciones:

1) Si tanx > 0 y tany > 0, tenemos: x = π/4, y = π/4.

2) Si tanx < 0 y tany < 0, tenemos: x = -π/4, y = -π/4.

Observa que hemos considerado valores de x e y pertenecientes al intervalo [0,2π].

Espero haberte ayudado.

Te ayudamos, Adriana:

Muchas gracias :3 
Disculpe, podría dibujar la gráfica del problema :c