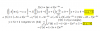-
Ariel Irigoyen
el 31/10/16 -
Marco Uraga
el 31/10/16 -
Agustina
el 31/10/16
Hola, tengo una consulta respecto al ejercicio 9.a) que pide analizar la derivabilidad de la función. Analicé el domino de cada parte de mi función y evalué la continuidad en el punto x=4, como me dio que era continua luego me fijé si es derivable en x=4, aplique la fórmula de cociente incremental y llegue a que los límites por derecha e izquierda no coinciden.mis dudas son:
Respecto al dominio : para la segunda porción de mi función, la que dice "20sen(x-4)..." llegué a que es (8/3 ; 4) U (4;+inf) , pero como esa porción está definida para x> 4 debo decir que el domino es R - {4}?
Respecto a la derivabilidad: el limite por izquierda me dio 3 y por derecha infinito ... no estoy segura de ese ultimo resultado, necesitaría una mano con ese.
Gracias de antemano.
-
KIMEUNWOOK
el 31/10/16
alguien me ayuda a resolver esto por metodo de coefieientes indeterminados, de ecuacione sdiferenciales
y``-3y`-10y=50cos5x-7e^-2x+12e^x+20x
David
el 31/10/16KIMEUNWOOK
el 31/10/16No creo que tenga que ver especificamente conun video tuyo, ya que en ningun momento encontre uno que combinara los tipos de soluciones, ademas no pido solucion ocmpleta solo preguntaba como debe ser la forma de la respuesta osea Yp:=Acosx+Bsenx+Ce^-2x+De^x+Ex.
Si hubiese un tipo de video donde las combinara no estaría aca preguntando.
gracias
-
leni
el 31/10/16Hola ..por favor me pueden ayudar con este ejercicio me piden el volumen....lo trate de sacar mediante envolventes cilíndricas . .creo q el planteamiento esta mal
-
Josue Mosh
el 31/10/16Tengo duda en cuanto a una derivada, es la de:
"f(x)=cos(|x|^3)"
Al derivar puedo obtener 2 expresiones jugando con las propiedades y obtengo:
f´(x)= (-3(x^2)*sin(|x^3|))/|x|
f´(x)=-3x|x|*sin(|x|^3|)
Mi problema es que al checar esta derivada en la calculadora de wolfram da como resultado:f´(x)=-3(x^2)*sen(x^3)
Y ni idea de como llegar a ese resultado, ¿alguien podría ayudarme? :/
-
Valentina Henao Velez
el 30/10/16hola tengo la funcion -x^3+2x^2 me piden factorizar,encontrar las raíces o ceros y tambien encontrar en que partes la grafica es negativa y positiva
Antonio Silvio Palmitano
el 31/10/16Tienes la expresión de la función: f(x) = - x³ + 2x² = extraemos factor común = - x² (x - 2). Observa también que el dominio es D = (-inf,+inf) = R, y que la función es continua.
Luego, planteamos la condición para una raíz: f(x) = 0, y por anulación de un producto tenemos dos opciones:
a) - x² = 0, que nos conduce a x1 = 0;
b) x - 2 = 0, que nos conduce a x2 = 2.
Luego, tenemos tres subintervalos para estudiar el signo, elegimos un representante para cada uno y evaluamos:
(-inf,0), representado por x = -1, para el que tenemos: f(-1) = - (-1)² (-1 - 2) = -1(-3) = 3 > 0, por lo que tenemos que la función toma valores positivos en este intervalo;
(0,2), representado por x = 1, para el que tenemos: f(1) = - 1² (1 - 2) = -1(-1) = 1 > 0, por lo que tenemos que la función toma valores positivos en este intervalo;
(2,+inf), representado por x = 3, para que el que tenemos: f(3) = - 3² (3 - 2) = -1(-1) = - 9*1 = - 9 < 0, por lo que tenemos que la función toma valores negativos en este intervalo.
Observa que x1 = 0 es una raíz de multiplicidad dos, por lo que no hay cambio de signo en los intervalos que ella limita.
Por lo tanto tenemos que la función es:
positiva en (-inf,0) u (0,2), y es negativa en: (2,+inf).
Espero haberte ayudado.
-
KIMEUNWOOK
el 30/10/16
hpla tengo una duda en el 5 b) en esa debo colocar como yp= Acosx+Bsenx +Ccosx +Dsenx, o debo simplemente utilizarla con la primera A y b es suficiente.este problema es d ecuacione sdiferenciales de metodos de coeficiente indeterminados.
no pido solucion, simplemente saber si para cada seno y coseno untilizo su forma de respuesta, o con una es basta.
Antonio Silvio Palmitano
el 31/10/16Observa que la ecuación característica asociada a la ecuación diferencial es: r² + 1 = 0, cuyas raíces son: r1 = i y r2 = -i, que corresponden a expresiones de seno y coseno con argumento x como tienes en el segundo miembro de la ecuación, por lo que la solución de la ecuación homogénea (y ' ' + y = 0) queda:
Yh = a*cosx + b*senx, con a y b números reales;
luego observa que la solución particular no debe tener la misma forma que la solución de la ecuación homogénea, por lo que planteamos:
Yp = Ax*cosx + Bx*senx, con A y B números reales que debemos determinar, luego derivamos:
Yp' = A*cosx - Ax*senx + B*senx + Bx*cosx, luego volvemos a derivar:
Yp' ' = - A*senx - A*senx - Ax*cosx + B*cosx + B*cosx - Bx*senx = - 2A*senx + 2B*cosx - Ax*cosx - Bx*senx.
Luego sustituimos en la ecuación diferencial y queda:
( - 2A*senx + 2B*cosx - Ax*cosx - Bx*senx ) + ( Ax*cosx + Bx*senx ) = 4*cosx - 2*senx, cancelamos términos opuestos a la izquierda y queda:
- 2A*senx + 2B*cosx = 4*cosx - 2*senx, luego comparamos coeficientes entre términos semejantes y queda el sistema de ecuaciones:
-2A = -2, de donde tienes: A = 1,
2B = 4, de donde tienes: B = 2;
y la solución particular de la ecuación diferencial queda:
Yp = x*cosx + 2x*senx;
y la solución general queda:
Y = Yh + Yp = a*cosx + b*senx + x*cosx + 2x*senx.
Espero haberte ayudado.
-
Nacho
el 30/10/16alguien me da una mano con este.
Antonio Silvio Palmitano
el 31/10/16Consideramos que el argumento de la integral es: at² + bt + c.
Integramos a la izquierda (indicamos con corchetes que debemos evaluar con regla de Barrow entre x y 1):
[ (⅓)at³ + (½)bt² + ct ] = 4x³ - 2x² - 2, evaluamos a la izquierda y queda la ecuación:
( (⅓)a + (½)b + c ) - ( (⅓)ax³ + (½)bx² + cx ) = 4x³ - 2x² - 2, distribuimos el agrupamiento, ordenamos términos a la izquierda y queda:
- (⅓)ax³ - (½)bx² - cx + ( (⅓)a + (½)b + c ) = 4x³ - 2x² - 2, luego comparamos términos semejantes y queda el sistema de ecuaciones:
- (⅓)a = 4, de donde tienes: a = - 12,
- (½)b = - 2, de donde tienes: b = 4,
- c = 0, de donde tienes: c = 0,
(⅓)a + (½)b + c = -2, que se verifica reemplazando los valores que hemos determinado en las ecuaciones anteriores.
Espero haberte ayudado.
-
Laura
el 30/10/16Hola,estoy cursando primero de carrera y no se como resolver este ejercicio referente a subespacios vectoriales. Se trata de comprovar si F es subespacio vectorial de M2x2. Gracias de antemano :)
F={A∈M2x2|A=(aa+b ba-b)}
David
el 31/10/16
