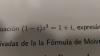Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Jose Manuel
el 31/10/16

Alguien me ayuda con el siguiente ejercicio?

••0 voto/s
•
David
el 2/11/16
Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. Lo siento de corazón… Espero lo entiendas

•0 voto/s
•

Cancelar
Maria del castillo
el 31/10/16

alguien me podría explicar cual es el lim de senx/x cuando tiende a infinito sin usar L'Hopital?

••0 voto/s
•
Antonius Benedictus
el 31/10/16
Es esto, María:

•0 voto/s
•

Cancelar
francisco escribano
el 31/10/16

ayuda por favor con funciones! cabe aclarar que no se puede usar calculadora

••0 voto/s
•
Antonius Benedictus
el 31/10/16
Te ayudamos, Francisco:

•0 voto/s
•

Cancelar
Karina
el 31/10/16

Hola tengo un problema de red lógica el cual no puedo desarrollarlo correctamente, ya que no me cohincide el resultado

••0 voto/s
•
David
el 2/11/16
Me encantaría ayudarte, pero no respondo dudas universitarias (o de asignaturas que no sean especificamente matemáticas, física o química) que no tengan que ver específicamente con los vídeos que ya he grabado como excepción. Lo siento de corazón… Espero lo entiendas

•0 voto/s
•

Cancelar
Mer
el 31/10/16

Alguien me puede ayudar a encontrar las raíces de la siguiente ecuación?

••0 voto/s
•
Antonio Silvio Palmitano
el 31/10/16
Comencemos por multiplicar por (1+i) en ambos miembros de la ecuación:
(1+i)(i-i)z³ = (1+i)², resolvemos y queda:
2z³ = 2i, hacemos pasaje de factor como divisor, resolvemos y queda:
z³ = i, expresamos a la unidad imaginaria en forma polar (observa que su módulo es 1 y que su argumento es 90°):
z³ = (1)(90°), hacemos pasaje d potencia como raíz (indicamos raíz cúbica con (3V))y queda:
z = (3V)( (1)(90°) ), aplicamos la fórmula de De Moivre para las raíces:
z = ( (3V)(1) )( (90° + 360°*k)/3 ), con k = 0, 1, 2,
resolvemos el módulo, distribuimos el denominador en el argumento y queda:
z = (1)( 30° + 120°*k ), con k = 0, 1, 2,
luego expresamos las raíces según los valores de k, resolvemos los argumentos y quedan (expresamos además en forma trigonométrica y en forma binómica::
z0 = (1)(30°) = cos30° + i*sen30° = V(3)/2 + (1/2)i,
z1 = (1)(150°) = cos150° + i*sen150° = - V(3)/2 + (1/2)i,
z2 = (1)(270°) = cos270° + i*sen270° = 0 - i.
Espero haberte ayudado.

•1 voto/s
•
Mer
el 31/10/16
Sólo una cosa, por qué su argumento es 90º?

•0 voto/s
•

Cancelar
fina
el 31/10/16

He visto todos los videos de racionalizazion de vuestro canal i no entiendo como hacer estos dos .
alguien me puede ayudar?? Gracias

••0 voto/s
•
Berlinne Claret Quispe Tapia
el 31/10/16
es simple completa a cuadrados los denominadores y multiplica el factor racionalizante en el numerador si no puedes aun asi avisa y te mando foto

•0 voto/s
•
Ángel
el 31/10/16
7/(1-√2) = 7(1+√2)/(1-√2)(1+√2) = (7+7√2)/(1-2) = -7-(7√2)

•0 voto/s
•

Cancelar
Albano Caminos
el 31/10/16

Buenas, quisiera que me dieran una mano con el punto c, muchas gracias!

••0 voto/s
•
Antonius Benedictus
el 31/10/16
Te ayudamos, Albano:

•0 voto/s
•

Cancelar
Alex Domínguez
el 31/10/16

Hola, me gustaría que me ayudaran con este ejercicio y me dijeran en que vídeo sale el proceso de la solución, ya que no lo entiendo ni consigo encontrar el vídeo, muchas gracias

••0 voto/s
•
Antonius Benedictus
el 31/10/16
la d):

•0 voto/s
•

Cancelar
Desconocido
el 31/10/16

Otra pregunta de probabilidad. Digamos que tenemos A₁A₂ y A₃que son compatibles.
En caso de que me pidan P((noA₁∩noA₂)UA₃) es posible decir que es lo mismo que P(noA₁∩noA₂∩noA₃)+P(A₃)?
He hecho un dibujo y es lo que me ha parecido.

••0 voto/s
•
Antonius Benedictus
el 31/10/16
¿Podrías poner foto del enunciado original?

•0 voto/s
•
Desconocido
el 31/10/16
Una empresa de ordenadores ha tomado parte en tres proyectos. Sea A_i≡' Ha adquirido el proyecto i ', i = 1,2,3 y P(A1) = 0.22, P(A2) = 0.25, P(A3) = 0.28, P(A1∩A2) = 0.11, P(A1∩A3) = 0.05, P(A2∩A3) = 0.07, P(A1∩A2∩A3) = 0.01. Calcula las siguientes probabilidades:
a) P(A1 U A2) (me ha salido 0.36)
b) P(noA1 ∩ noA2) (me ha salido 0.64)
c) P(A1 U A2 U A3) (me ha salido 0.53)
d) P(noA1 ∩ noA2 ∩ no A3) (me ha salido 0.47)
e) P(noA1 ∩ noA2 ∩ A3) (me ha salido 0.17)
f) P((noA1∩noA2)UA₃) (aqui la pregunta, me ha salido 0.75)

•0 voto/s
•
Antonius Benedictus
el 31/10/16
Ceo que es todo correcto:

•0 voto/s
•

Cancelar
Magalí
el 31/10/16

Alguien me puede decir si está bien resuelta la integral

••0 voto/s
•
David
el 31/10/16
PERFECTA!!!!! :D Gran trabajo...

P.D. Cuando escribas una integral no olvides siempre, siempre añadir al final dx...
Por ejemplo, ∫x es incorrecto... ∫x .dx es correcto...

•1 voto/s
•

Cancelar