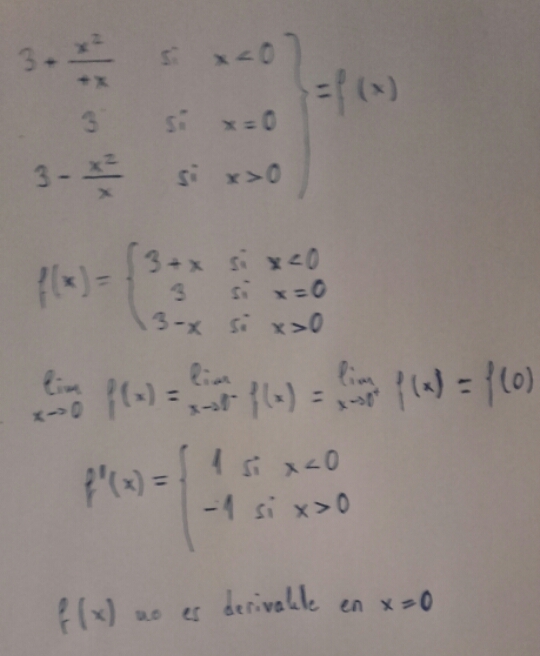-
Usuario eliminado
el 31/10/16Hola,
Tengo este problema a resolver pero estoy totalmente perdida.
Gracias
Antonio Silvio Palmitano
el 31/10/16Comencemos por denominar b = - 0,00012, y la expresión de la función queda:
N(t) = No * e^bt.
Luego, nos dicen que la cantidad de C14 en la muestra ha disminuido un 20%, por lo que tenemos que ha conservado un 80%, y a la cantidad de isótopo que ha conservado la escribimos:
a) N(t) = (80/100)No = 0,8No.
Luego sustituimos en la expresión de la función y queda:
0,8No = No * e^bt, cancelamos el factor común No y queda:
0,8 = e^bt, tomamos logaritmo natural en ambos miembros y queda:
ln0,8 = bt, reemplazamos el valor de b y queda:
ln0,8 = -0,00012t, hacemos pasaje de factor como divisor y queda:
ln0,8 / (-0,00012) = t, resolvemos con calculadora y queda:
b) t = 1859,53 años (aproximadamente).
Espero haberte ayudado.
-
Nacho
el 31/10/16hola alguien ma yuda a calcular el valor de alfa para que se cumpla que el Area 1 sea igual al area 2 (roja y verde). Sabiendo que l a funcion va de [0,a]
me da que es 3. pero tiene que ser algo con fraccion , segun las soluciones.
hice la integral de h(x)-g(x) (evaluado en a y 0) por barrow y eso lo iguale a la integral de g(x) -f(x)
por las dudas que no se entienda la letra:
h(x) = (alfa)x^2
g(x)= 2x^2
f(x)= x^2
Antonio Silvio Palmitano
el 31/10/16Por favor, envía foto con el enunciado para que podamos ayudarte.
Observa que todos los tramos de gráficas de las funciones f, g y h tienen un extremo en común en el origen de coordenadas, pero no tienen extremo en común para x = a, ya que las funciones toman distintos valores:
f(a) = a², g(a) = 2a² y h(a) = αa²,
y observa que no se corresponde tu dibujo con ellos.
-
Genesis Guzman
el 31/10/16Nose como realizar la parte final de este ejercicio
-
Ángel
el 31/10/16Hola,
si me piden estudiar la derivabilidad y la expresión de la función derivada de:
f(x)= 3-( x2÷ |x| ) si x≠0
3 si x=0
¿para la derivabilidad se haría esto?
La expresión de la función derivada no sé como calcularla
Gracias
Antonio Silvio Palmitano
el 31/10/16 -
Paula
el 31/10/16Ayuda, Antonio Benito.
Expresa el 2º miembro de cada igualdad como un solo logaritmo y halla los valores de B,X,Y.
log B= 3+4*log a -2*log b
log en base 3 de X= log en base 3 de 5- 3log en base 3 de 2- 2 log en base 3 de 4
log en base 5 de Y= 2 log en base 5 de a+ 3 log en base 5 de 2 -4
Antonio Silvio Palmitano
el 31/10/161) Tienes:
logB = 3 + 4loga - 2logb (observa que log(1000) = 3) aplicamos propiedad de los logaritmos de potencias en los dos últimos términos y queda:
logB = log1000 + log(a^4) - log(b^2), aplicamos propiedad del logaritmo de un producto en los dos primeros términos y queda:
logB = log(1000a^4) - log(b^2), aplicamos propiedad del logaritmo de una división y queda:
logB = log( 1000a^4 / b^2 ), luego comparamos argumentos de los logaritmos y llegamos a:
B = 1000a^4 / b^2.
2) Indicamos logaritmo en base 3 como Log.
LogX = Log5 - 3Log2 - 2Log4, aplicamos propiedad del logaritmo de una potencia en los dos últimos términos y queda:
LogX = Log5 - Log(2^3) - Log(4^2), resolvemos los argumentos, y queda:
LogX = Log5 - (Log8 + Log16), aplicamos propiedad del logaritmo de un producto en el agrupamiento y queda:
LogX = Log5 - Log(8*16), resolvemos el segundo argumento, aplicamos propiedad del logaritmo de una división y queda:
LogX = Log(5/128), comparamos argumentos y llegamos a:
X = 5/128.
3) Indicamos logaritmo en base 5 como LOG.
LOGY = 2LOGa + 3LOG2 - 4 (observa que LOG(3125) = LOG(5^4) = 4), aplicamos propiedad del logaritmo de una potencia en los dos primeros términos y queda:
LOGY = LOG(a^2) + LOG(2^3) - LOG(3125), resolvemos el segundo argumento, aplicamos propiedad del logaritmo de un producto en los dos primeros términos y queda:
LOGY = LOG(8a^2) - LOG(3125), aplicmos propiedad del logaritmo de una división y queda:
LOGY = LOG( 8a^2 / 3125 ), comparamos argumentos y llegamos a:
Y = 8a^2 / 3125.
Espero haberte ayudado.
-
Genesis Guzman
el 31/10/16Tengo una duda en este ejercicio, nose si he derivado mal, pero nose donde incluir ese "2" que ha dado al derivar Z... Estaba viendo si podia expresar asi: Z' = -2y'/y^3 yo lo pondria asi -2Z' se puede poner asi?
Antonio Silvio Palmitano
el 31/10/16 -
Bruno
el 31/10/16Por favor si alguien me ayuda con esto.. La segunda derivada de Y, de x² − y² = 1 ?
Antonio Silvio Palmitano
el 1/11/16Si mantenemos la ecuación implícita, derivamos con respecto a x:
2x - 2y*y ' = 0, dividimos por 2 en todos los términos de la ecuación y queda:
x - y*y ' = 0, hacemos pasaje de término y queda:
- y*y ' = - x, multiplicamos por -1 en ambos miembros y queda:
y*y ´ = x (*), luego volvemos a derivar (observa que a la izquierda tenemos un producto):
y ' * y ' + y * y ' ' = 1, escribimos el primer término como potencia y queda:
( y ' )² + y * y ' ' = 1 (**).
Luego, a partir de la ecuación señalada (*) podemos despejar: y ' = x/y, sustituimos en la ecuación señalada (**) y queda:
(x/y)² + y * y ' ' = 1, distribuimos la potencia en el primer término y queda:
x² / y² + y * y ' ' = 1, multiplicamos en todos los términos de la ecuación por y² y queda:
x² + y³ * y ' ' = y², hacemos pasaje de término y queda:
y³ * y ' ' = y² - x² (***).
Luego, puedes volver a la ecuación implícita inicial y puedes despejar: y = V(x² - 1), luego sustituyes en la ecuación señalada (***) y podrás despejar una expresión explícita de la derivada segunda de y como función de x.
Espero haberte ayudado.
-
Alex Domínguez
el 31/10/16
-
Marcos
el 31/10/161)Hallar los valores de a y b para que la siguiente funcion sea continua
en y derivable en x = 1
f(x) =
x
^2 + a si x > 1
bx^2 − 2a si x ≤ 12) Dada g(x) = 5f(x) (3x² + 1) y sabiendo que f(2) = 1 y f´(2) = 3.
Hallar g´(2).Saludos
Ángel
el 15/11/16Disculpa por mi despiste, deriVada de 2a=0....no me he dado cuenta hasta hoy, que recibí flag
Reenvío subsanando mi error:
Para que sean contínuas se debe cumplir que:
12+a= b*12-2a
a=(b-1)/3
f´(x)= 2x si x>1 y 2bx si x<1
Para que sean derivables se debe cumplir que:
2b=2
b=1
a= (1-1)/3= 0=a
SERÁ CONTÍNUA Y DERIVABLE PARA a=0 Y b=1
-
Usuario eliminado
el 31/10/16
