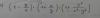-
Javier García
el 19/10/16Me pueden decir como se hace? Se hacer este tipo de ejercicios, pero este me ha dado muchas dudas... Gracias
Antonio Silvio Palmitano
el 19/10/16Primero puedes extraer denominadores comunes en todos los factores, y la expresión queda:
(x - y)/x * (x + y)/y * (x^2 - y^2 + y^2)/(x^2 - y^2) =, resuelves el numerador en el tercer factor, factorizas su denominador y queda:
= (x - y)/x * (x + y)/y * ( x^2 / (x+y)(x-y) ) =, luego multiplicas numeradores entre si, y denominadores entre si y queda:
= (x-y)(x+y)*x^2 / xy(x+y)(x-y) =, simplificamos factores y llegamos a:
= x/y.
Espero haberte ayudado.
-
Patricia Muñoz
el 19/10/16M epiueden ayudar con el b) .??
Antonio Silvio Palmitano
el 19/10/16Observa que en el numerador (N) tienes dos factores con diferencias de cuadrados, factorizas y queda:
N = (x+3)(x-3)(y+4)(y-4)
Observa que en el tercer factor en el denominador (D) puedes extraer factor común, lo haces y queda:
D = 2xy(x-3)(y+4)^2.
Luego simplificas factores y la expresión queda:
N/D = (x+3)(y-4) / 2xy(y+4).
Espero haberte ayudado.
-
Javier Jiménez
el 19/10/16Hola, por favor me podrías ayudar a calcular la continuidad de esta función:
f(x)= (x/x-1) - (1/ln(x)) si x es distinto de 1
f(x)=1, si x es igual a 1
Gracias
Antonio Silvio Palmitano
el 19/10/16La función está definida para x = 1, y f(1) = 1
Luego, debes plantear el límite de la función para x tendiendo a 1. Una forma para calcularlo es aplicar la regla de L'Hôpital (en este caso dos veces, y queda que el límite es igual a 1/2.
Luego, puedes concluir que la función es discontinua evitable (no esencial) en x = 1.
Espero haberte ayudado.
-
Marta Gimeno
el 19/10/16buenas estoy haciendo el rango de una matriz cuadrada de orden tres mediante determinantes pero cuando el valor es 0 no se determinar si es de rango 1 o 2. ¿Cómo se hace?
(1 1 1)
(2 1 3)
(1 0 1)
se que el rango es 2 ya que la fila 2 es una suma de la primera fila mas la tercera. A sí que en este caso es facil pero cuando es mas complicado como lo deducimos?
Antonio Silvio Palmitano
el 19/10/16Por favor, verifica que estén correctamente escritos los elementos de la matriz, porque, observa, el tercer elemento de la fila 2 no es igual a la suma de los terceros elementos de las otras dos filas.
Pero, si el determinante de la matriz fuese igual a cero, ya sabes que el rango no es tres.
Luego, puedes elegir un subdeterminante (por ejemplo, el que tiene orden dos y está formado por los dos primeros elementos de la segunda y tercera fila):
(2 1)
(1 0)
Luego, calculas el determinante, que en este caso es igual a -1 y, como es distinto de 0, podemos concluir que el rango de la matriz es 2.
Espero haberte ayudado.
-
Usuario eliminado
el 19/10/16
Hola unicoos, que alguien me diga cómo se deduce que 1 + 2 + 3 + 4 + 5 + ... = -1/12, por favor.
Jordi García
el 19/10/16Si estás sumando números enteros positivos es imposible que la solución sea negativa. Pon el enunciado original. En caso de que te digan el extremo de la suma y no te den el resultado, por ejemplo, 1+2+3...100 tienes que sumar los extremos, dividir el último número por 2 y multiplicarlo por la suma que has hecho al principio. Sumamos porque se cumple la siguiente equivalencia: 1+100=2+99=3+98... De manera que si juntamos todos los números obtenemos 50 parejas que suman 101, así que 50*101=5050. (solo si se pueden agrupar todos los números sin que sobre ninguno, es decir, que tengas un número par de números).
Saludos.
-
Angie Criollo Zuñiga
el 19/10/16hola, ¿alguien me podría decir si este ejercicio está bien resuelto?
Ángel
el 19/10/16Bien resuelto no está porque su sustituyes los valores de x, y, z que has obtenido en el sistema de ecuaciones original no concuerdan los resultados
¿Fallo que haya visto? De momento en el primer paso de reducción: (-3x-9y+9z=3) + (3x-y+2z=4) es igual a -10y+11z= 7...y no 10y-11z=7
Angie Criollo Zuñiga
el 19/10/16
Ángel
el 19/10/16
Ángel
el 19/10/16 -
Rafa
el 19/10/16 -
Lucero Viña Cabrera
el 19/10/16Hola Unicoos,
necesito sacar la segunda derivada de P': -3120/x^2 + 2 para un ejercicio de optimización. Me podrian ayudar? Gracias!
Antonio Silvio Palmitano
el 19/10/16 -
Jordi García
el 19/10/16Hola UNICOOS, ¿cómo se hace este ejercicio?
Encuentra un polinomio P(x) de segundo grado cuyas raíces sean 1 y -2 y tal que P(3) = 30.
Problema del día (OPCIONAL):
Si tengo 3 cajas mal etiquetadas:
1ª caja: caramelos de limón
2ª caja: caramelos de fresa
3ª caja: caramelos de fresa y caramelos de limón (mezclados)
¿Cuántos caramelos tengo que probar como mínimo para etiquetar correctamente las cajas?
Ángel
el 19/10/16No sé como hacerlo para que P(3)=30...a ver si alguien puede sacarte de dudas, yo te ayudaré con la parte "Encuentra un polinomio P(x) de segundo grado cuyas raíces sean 1 y -2", es decir, reconstruir una función cuadrática a partir de sus raíces: se utiliza la siguiente fórmula general
X^2 - (x1+x2)X + x1x2 =0
sustituimos x1=1, x2=-2 y nos queda:
x^2 - (-1)x + (-2) =0
x^2 + x - 2=0 -------------------> Polinomio de 2º grado con raíces 1 y -2
...y en el" problema del día" basta con coger 1 caramelo de la 3ª caja :D:D porque:
1ª opción: Si sale uno de limón...la 2ª serán mezlados y la 1ª de fresa (y la 3ª de limón obviamente, porque son o de fresa o limón, NO MEZLA, ESTAN MAL ETIQUETADAS TODAS)
2ª opción: Si sale uno de fresa la 1ª será de mezcla y la 2ª de limón (y la 3ª de fresa :p)
-
dovigame
el 19/10/16Hola únicos por favor quiero que me ayuden con este ejercicio precisamente el apartado a,es que lo he hecho pero no creo que está bien.He hallado la función primera derivada,lo he evaluado en la abcisa x=π/6 ,sabiendo que la función primera derivada es cosx,al evaluar la abcisa esta me da como resultado 0.86 y esto es muy fiable para mi ,me parece que hay una trampa que tengo que descubrir y no la sé, por eso OS pido ayuda.Y otra cosa mas he ganado una medalla de 5 dedos es decir la palma de la mano quisiera saber su importancia.
Matías Ignacio Loyola Galdames
el 19/10/16Lo que hiciste está bien, pero con eso sacas la pendiente de la recta tangente al gráfico en ese punto.
Ahora necesitas un punto de la recta, evalúas en π/6.
Y=sen(x)
y=sen(π/6)=0.5
Entonces la recta pasa por (π/6,0.5)
Usando la ec: y-y1=m(x-x1) Siendo m, la pendiente e (x1,y1) un punto de la recta.
y-0.5=0.86(x-π/6)
pd: en la parte de abajo de la página sale la opción medallas, ahí las ves.
